Introduction
The goal of this article is to introduce the gradient theorem of line integrals and to explain several of its important properties. In the first section, we will present a short interpretation of vector fields and conservative vector fields, a particular type of vector field. Here, we will consider the essential role of conservative vector fields. Moreover, we will also define the concept of the line integrals.
In the next section, we will describe the fundamental theorem of line integrals. We will examine the proof of the theorem.
Then, we will speak about the significant consequences of the gradient theorem. Most importantly, we will consider the path-independence of line integrals.
In the end, a straightforward and detailed example will help us put everything in practice.
Preliminaries
Recall the fundamental theorem from introductory, single-variable calculus that allows us to integrate a function that is the derivative of another function. Mathematically speaking, this can be written as follows:
If F \left(x \right) = f^{\prime} \left( x \right) ,
then according to the fundamental theorem, the integral of F \left(x \right) is
\int_a^b F \left(x \right) dx = \int_a^b f^{\prime} \left( x \right) dx = f \left( b \right) - f \left( a \right) .
In this article, we will consider a similar theorem for line integrals of vector fields. First, we will present some details on vector fields and line integrals.
Definition 1:
A line integral is an integral of a function taken over a curve.
Let the curve S be given by the vector function s \left( t \right) , with \bar{a} = s \left( a \right) and \bar{b} = s \left( b \right) . Then, the line integral can be written as
\int_S F \cdot ds = \int_a^b F \left( S(t) \right) \cdot S^{\prime}(t) dt ,
and equivalently, the line integral can also be written as follows:
\int_S F \cdot ds = \int_C F_1 dx + F_2 dy + F_3 dz , with
F = \left( F_1 \left( x \right), F_2 \left( x \right), F_3 \left( x \right) \right) .
Definition 2:
A vector field is a map, F:R^n to R^n , which assigns every value of x to a vector, F \left( x \right) .
Further, there is a particular kind of vector field that plays an essential role in calculating the line integral of vector fields. This kind of vector fields are called conservative vector fields. Below, we will define conservative vector fields.
Definition 3:
If the vector field F is the gradient of a function f , then F is called a gradient or a conservative vector field. The function f is called the potential or scalar of F .
The Gradient Theorem of Line Integrals
Now, we are ready to discuss the gradient theorem of line integrals. This theorem is also called the fundamental theorem of line integrals because of its similarity to the theorem in single-variable calculus with the same name.
Theorem:
Let F = \Delta f be a conservative vector field. Then, the line integral of F over a curve S from A to B is evaluated with the difference of the potential function values at the endpoints. Mathematically,
\int_S \Delta f \cdot ds = f \left( B \right) - f \left( A \right) .
Proof:
According to the definition of line integral above, we can write
\int_S \Delta f \cdot ds = \int_a^b \Delta f \left( s(t) \right) \cdot s^{\prime} \left( t \right) dt ,
for the parametrization
A = s \left( a \right) and B = s \left( b \right) with a < t < b .
Then, applying the multivariate chain rule gives
\dfrac{d}{dt} \left( f \left( s (t) \right) \right) = \Delta f \left( s(t) \right) \cdot s^{\prime} \left( t \right) .
Moreover, the fundamental theorem from single-variable calculus tells us that
\int_a^b \dfrac{d}{dt} \left( f \left( s (t) \right) \right) dt = f \left( s \left( b \right) \right) - f \left( s \left( a \right) \right) .
The last expression is equivalent to the following, in terms of the original curve S :
\int_S \Delta f \cdot ds = f \left( B \right) - f \left( A \right) .
Thus, we have proved the generalized form of the fundamental theorem of calculus, the gradient theorem.
Consequences of the Fundamental Theorem
In this section, we will demonstrate several important implications and provide some remarks related to the fundamental theorem of line integrals.
Corollary 1:
The integral of a conservative field is path-independent.
Corollary 2:
The integral of a conservative field over a closed curve is zero.
Remark:
It turns out that a potential function f exists if and only if the field F is conservative; that is, path-independent.
The last remark allows us to compute a line integral by using the gradient theorem. To do so, we must perform the following two steps: find out if F is conservative, and if it is, find the potential function f .
An Application of the Gradient Theorem
Let’s consider an example that illustrates all the details of applying the gradient theorem.
Example:
Consider f \left( x, y \right) = xy^2 , given that F is conservative. As a result, F \left( x, y \right) = \delta f \left( x, y \right) = \left( y^2, 2xy \right) . We are required to compute the line integral of the field F over the curve C , given as c \left( u \right) = \left( u^2, 2 \left(u - 2 \right)^3 \right) for 1 \leq u \leq 3 . This means that the starting point of the curve C is a = c(1) = \left( 1, -2 \right) and the ending point is b = c \left( 3 \right) = \left( 9, 2 \right) .
We can evaluate the required integral in two ways: We can use the gradient theorem or we can compute the integral directly.
First, by the gradient theorem of line integrals, we obtain
\int_C F \cdot dc = f \left( 9, 2 \right) - f \left( 1, -2 \right) = 36 - 4 = 32 .
Second, the direct way would give the following:
\int_C F \cdot dc = \int_a^b F \left( c \left( u \right) \right) \cdot c^{\prime} \left( u \right) du
= \int_1^3 F \left( u^2, 2 \left( u - 2 \right)^3 \right) \cdot \left( 2u, 6 \left( u - 2 \right)^2 \right) dt
= \int_1^3 8 \left( u \left( u - 2 \right)^6 + 3 u^2 \left( u - 2 \right)^5 \right) dt
= 8 \left( 32 u^2 - 96 u^3 + 120 u^4 - 80 u^5 + 30 u^6 - 6 u^7 + \left. \frac{u^8}{2} \right) \right|_1^3
= 32 .
As expected, we have obtained the same result with both methods.
Recall that F is conservative, or in other words, path-independent. This means that the value of the integral should not depend on the curve. To show this in practice, we will consider a new curve with the same starting and ending points and compute the integral over that curve. We want to show that we would still get the same result. The starting and the ending points of the curve C are \left( 1, -2 \right) and \left( 9, 2 \right) . Let’s consider the line B , which is a straight line starting and ending at the same points as C . The line B is parametrized as follows:
d \left( u \right) = \left( 1, -2 \right) + u \left( 8, 4 \right) = \left( 1 + 8u, 4u - 2 \right) for 0 \leq u \leq 1 . The figure below shows the two curves, C in blue and B in green.

Let’s now compute the line integral over curve B :
\int_B F \cdot db = \int_0^1 F \left( d \left( u \right) \right) \cdot d^{\prime} \left( u \right) du
= \int_0^1 F \left( 1 + 8u, 4u - 2 \right) \cdot \left( 8, 4 \right) du
= \int_0^1 \left( 4 - 16u + 16 u^2, -4-24u+64 u^2 \right) \cdot \left( 8, 4 \right) du
= \int_0^1 16 \left( 1 - 14 u + 24 u^2 \right) du
= 32 .
Finally, we get the same result, which shows the path-independence for the line integral.
Conclusion
This article presented an essential theorem of calculus: the fundamental theorem of vector fields, also known as the gradient theorem. In the beginning, we defined the terms that we must know to understand the theorem. Then, we considered the theorem and proved it. Per the theorem, the line integral of a conservative vector field over a curve can be evaluated by the values of the potential function at the starting and ending points of the curve. The path-independence of the integral is an important result, not only for further topics in calculus but also for physics, economics, and many other spheres.
Afterward, we examined the consequences of the gradient theorem. A straightforward and detailed example was presented to show the application of the theorem.
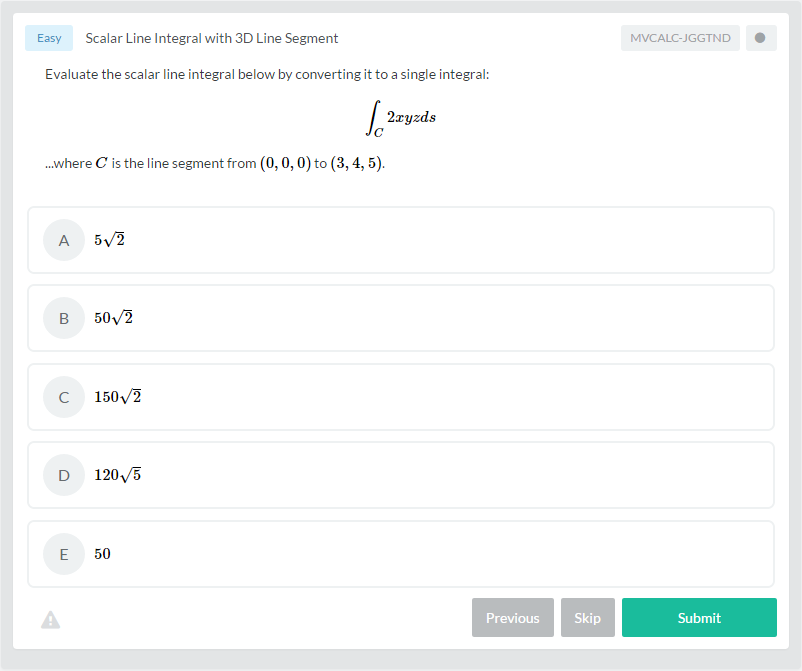
Let’s put everything into practice. Try this Multivariable Calculus practice question:
Looking for more Multivariable Calculus practice?
You can find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery in Multivariable Calculus.
Start practicing here.
Are you a teacher or administrator interested in boosting Multivariable Calculus student outcomes?
Learn more about our school licenses here.