Derivatives measure how a function changes at any specific point. However, it is not always possible to rely on standard differentiation rules. When faced with unknown or complicated functions, it helps to estimate the similar idea of a tangent’s slope by looking at a nearby secant line. Consequently, AP® Calculus AB-BC devotes a portion of coursework to numerical methods. These methods, covered in 2.3 Estimating derivatives, show how to interpret data from a derivative table or set up difference quotient formulas for better approximations.
What We Review
What Is a Derivative?
Fundamental Idea of a Derivative
A derivative represents the instantaneous rate of change of a function. In more concrete terms, consider a function f(x). Its derivative at a point x = a is the slope of the tangent line to f(x) at x = a. Symbolically, it is found by taking a limit of the difference quotient:
\displaystyle f'(a) = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h}This expression captures how rapidly (and in which direction) f(x) is changing at x = a.
Importance of Estimating Derivatives
Occasionally, the limit definition is not workable, or the function formula is missing. In those cases, a numerical approach helps. By choosing nearby points on a derivative table or using small increments h, an approximate slope can be calculated. This approach is especially helpful for analyzing experimental data or complicated functions where official derivative formulas are not obvious.
Approaches to Estimating Derivatives
Difference Quotients
The difference quotient is the standard tool for approximating a rate of change:
\displaystyle \frac{f(x + h) - f(x)}{h}When h is very small, the slope of the secant line closely matches the slope of the tangent line. However, it is important to pick an h that is small enough to capture local behavior but not so small that calculator error becomes significant. The image below shows how smaller values of h approach the tangent line at a given point.
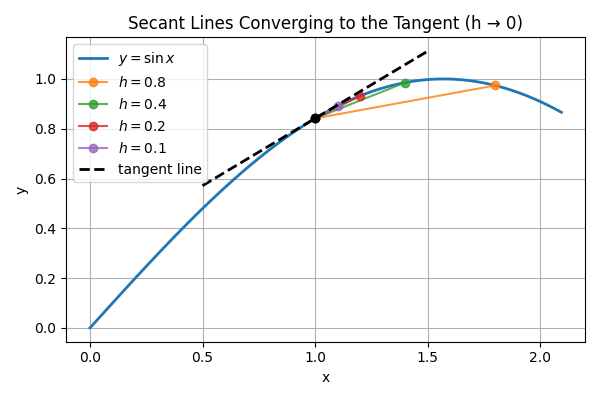
Symmetrical Difference Quotients
A symmetrical difference quotient tries to reduce error by looking at points equally spaced around x. Instead of using x and x + h, this method uses x + h and x - h:
\displaystyle \frac{f(x + h) - f(x - h)}{2h}This technique often yields a more precise estimate because the average of values on both sides of x reduces some issues caused by uneven rates of change or round-off.
Using a Derivative Table
A derivative table is typically a collection of points showing x-values along with corresponding f(x)-values. If data is reasonably close, it is possible to find a good approximation of the derivative by using difference quotients with the table’s information. However, always check for consistency. If the values look erratic or widely spaced, the estimate might have large error.
Example 1: Estimating from Tabulated Data
Suppose there is a derivative table for a function f(x), providing these data points:
| x | f(x) |
|---|---|
| 1.9 | 3.00 |
| 2.0 | 3.14 |
| 2.1 | 3.26 |
| 2.2 | 3.36 |
Estimate f'(2.0) using a difference quotient.
- Identify the closest values around x = 2.0. Here, x=1.9 and x=2.1 are closest.
- Apply the difference quotient for x = 2.0 using h = 0.1: \displaystyle \frac{f(2.0 + 0.1) - f(2.0)}{0.1} = \frac{f(2.1) - f(2.0)}{0.1} = \frac{3.26 - 3.14}{0.1} = \frac{0.12}{0.1} = 1.2
- Conclude that f'(2.0) \approx 1.2.
Practice Problem:
Using the same table, estimate f'(2.1) with h = 0.1.
Step-by-Step Solution (Practice):
- Identify the relevant points around 2.1, which are x=2.0 and x=2.2.
- Use the difference quotient: \displaystyle \frac{f(2.1 + 0.1) - f(2.1)}{0.1} = \frac{f(2.2) - f(2.1)}{0.1} = \frac{3.36 - 3.26}{0.1} = \frac{0.10}{0.1} = 1.0
- The approximate derivative is f'(2.1) \approx 1.0.
Example 2: Using Symmetrical Difference
Now consider a second dataset for a function g(x). The values near x=5 are:
| x | g(x) |
|---|---|
| 4.9 | 6.10 |
| 5.0 | 6.20 |
| 5.1 | 6.29 |
| 5.2 | 6.37 |
Find g'(5.0) using the symmetrical difference quotient with h=0.1.
- Choose the points x=4.9 and x=5.1, which are 0.1 units away from 5.0.
- Apply the formula: \displaystyle \frac{g(5.0 + 0.1) - g(5.0 - 0.1)}{2 \cdot 0.1} = \frac{g(5.1) - g(4.9)}{0.2}
- Substitute the values: \displaystyle \frac{6.29 - 6.10}{0.2} = \frac{0.19}{0.2} = 0.95
- Conclude that g'(5.0) \approx 0.95.
- Notice how a symmetrical difference usually provides a more balanced approach compared to one-sided estimates.
Practice Problem:
Using the symmetrical difference quotient technique, estimate g'(5.1) with h=0.1.
Step-by-Step Solution (Practice):
- Use x = 5.1, with points 5.1 - 0.1 = 5.0 and 5.1 + 0.1 = 5.2. If g(5.2) = 6.37, then:
- Compute: \displaystyle \frac{g(5.1 + 0.1) - g(5.1 - 0.1)}{2 \cdot 0.1} = \frac{g(5.2) - g(5.0)}{0.2} = \frac{6.37 - 6.20}{0.2} = \frac{0.17}{0.2} = 0.85
- Thus, g'(5.1) \approx 0.85.
Quick Reference Chart: Key Terms and Definitions
| Term | Definition |
| Derivative | The rate of change of a function at a specific point, often found using the limit of the difference quotient. |
| Difference Quotient | An expression for estimating the slope of a secant line: \frac{f(x + h) - f(x)}{h}. |
| Symmetrical Difference | A method that uses points equally spaced around x to improve accuracy: \frac{f(x + h) - f(x - h)}{2h}. |
| Average Rate of Change | The slope of the secant line between two points, giving an approximate slope over an interval. |
| Instantaneous Rate of Change | The exact slope of the tangent line at a single point, represented by the derivative. |
Conclusion
Estimating derivatives is a key part of calculus. In fact, 2.3 Estimating derivatives introduces practical strategies for finding approximate slopes, especially when direct methods are unavailable. Therefore, using a derivative table, difference quotients, or symmetrical difference enhances understanding of how functions behave. Moreover, analyzing numerical data from these approaches can reinforce broader calculus concepts, such as continuity and limits.
These techniques serve as building blocks for more advanced topics in AP® Calculus AB-BC. Ultimately, with careful attention to choosing appropriate h values and verifying the consistency of data points, one can effectively gain insight into a function’s rate of change.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 2.2 Defining the Derivative of a Function and Using Derivative Notation
- 2.4 Connecting Differentiability and Continuity: Determining When Derivatives Do and Do Not Exist
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








