Introduction to Calculus Limits

Calculus limits form the foundation for much of the work in AP® Calculus AB-BC. In simple terms, a limit describes the value a function approaches as its input (often x) moves toward a certain number. Calculus limits practice helps solidify this understanding and paves the way for derivatives and integrals, which are central to advanced topics in calculus.

However, it is essential to master limit concepts early, because understanding them simplifies many later lessons. Therefore, strong calculus limits practice helps develop the skills needed for success on the AP® exam and beyond.

How Limits Fit into AP® Calculus AB-BC

Limits connect closely to derivatives, since the derivative is defined in terms of a limit. This means that limits appear throughout the course of AP® Calculus AB-BC, from the earliest lessons on slope to more complex problems involving rates of change. Consequently, regular “calculus limits practice” will build confidence and reduce confusion when higher-level concepts appear.

Foundational Concepts

Direct Substitution Principle

When a function is continuous at a particular x-value, a limit at that point can often be found by direct substitution. Simply replace x with the point of interest.

• If f(x) = x^2 - 1, then the limit as x approaches 2 can be found by substituting 2 into x^2 - 1.

Example: Direct Substitution

Evaluate \lim_{x \to 2} (x^2 - 1).

Step-by-Step Solution:

1. If the function is continuous for x = 2, attempt direct substitution.
2. Substitute x = 2 into x^2 - 1. This gives 2^2 - 1 = 4 - 1 = 3.
3. Therefore, \lim_{x \to 2} (x^2 - 1) = 3.

Practice Problem (Try It):

Find \lim_{x \to 3} (3x + 1).

• Substitute x = 3 directly.
• Confirm the function is continuous at x = 3.
• Evaluate the limit. (Solution: \lim_{x \to 3} (3x + 1)=10.

Factoring and Simplification

Sometimes, direct substitution gives an indeterminate form like \frac{0}{0}. In such cases, factoring helps simplify the expression and remove problematic factors. Common factorizations, such as factoring out common terms or using difference of squares, remain impactful in “calculus limits practice” because they often reveal cancellations.

Example: Factoring Technique

Evaluate \lim_{x \to 3} \frac{x^2 - 9}{x - 3}.

Step-by-Step Solution:

1. Substitute x = 3 directly to check if it is valid. That yields \frac{0}{0}, an indeterminate form.
2. Factor the numerator: x^2 - 9 = (x - 3)(x + 3).
3. Simplify: \frac{(x - 3)(x + 3)}{x - 3} = x + 3, provided x \neq 3.
4. Now substitute x = 3 into x + 3. This evaluates to 6.
5. Therefore, \lim_{x \to 3} \frac{x^2 - 9}{x - 3} = 6.

Practice Problem (Try It):

Find \lim_{x \to 1} \frac{x^2 - 1}{x - 1}.

Hint: Factor out the numerator and simplify before substituting x = 1. Solution \lim_{x \to 1} \frac{x^2 - 1}{x - 1}=2.

Special Techniques and Rules for Limits

Identifying the Appropriate Procedure

It is vital to classify the problem early. Determining if direct substitution fails, factoring is possible, or the function is a rational expression helps in choosing the correct procedure. For instance, consider whether a conjugate multiplication technique might help for radicals, or if an indeterminate form requires L’Hôpital’s Rule.

L’Hôpital’s Rule

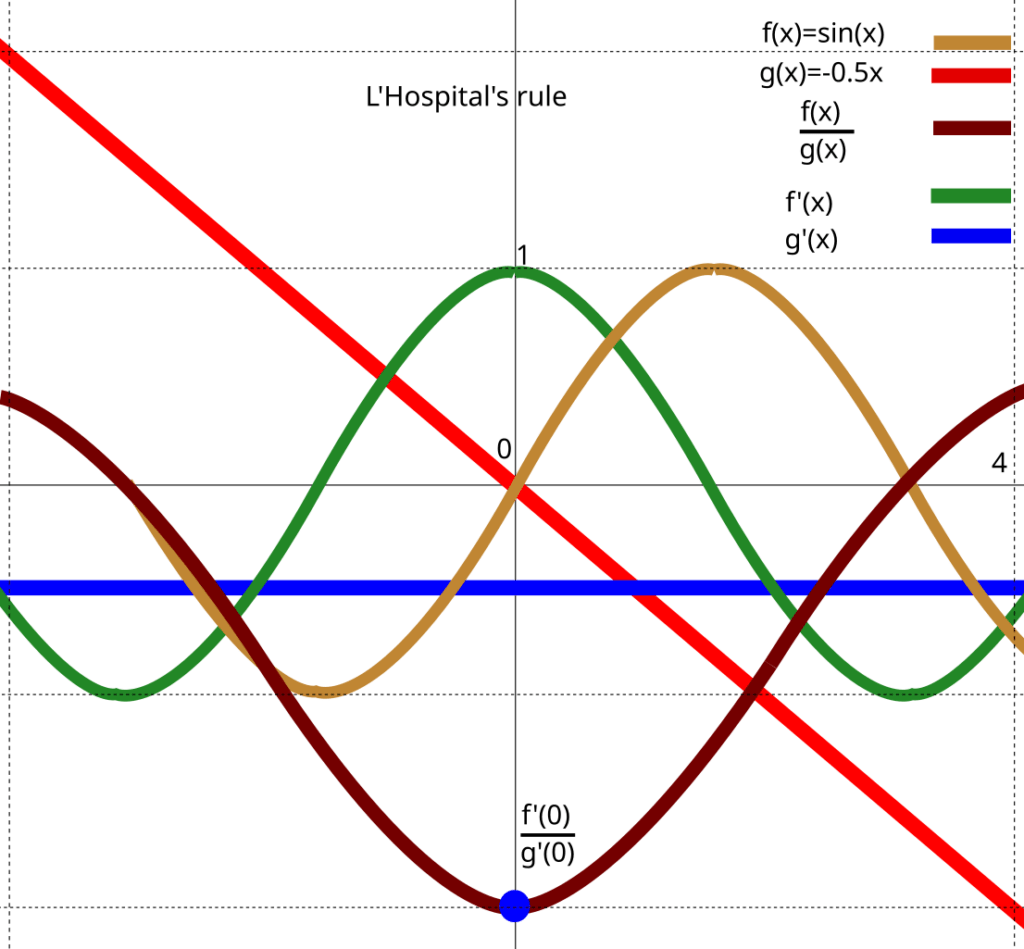
When substitution leads to \frac{0}{0} or \frac{\infty}{\infty}, L’Hôpital’s Rule can be used. This rule says that \lim_{x \to a} \frac{f(x)}{g(x)} can be turned into \lim_{x \to a} \frac{f'(x)}{g'(x)}, provided all conditions are met. The image below shows a visual example of L’Hopital’s rule with the limit \lim_{x \to 0} \frac{\sin x}{-0.5x}

Example: L’Hôpital’s Rule

Evaluate \lim_{x \to 0} \frac{\sin x}{x}.

Step-by-Step Solution:

1. Use direct substitution: \frac{\sin 0}{0} = \frac{0}{0}, an indeterminate form.
2. Apply L’Hôpital’s Rule. Differentiate the numerator and denominator separately:
   • \frac{d}{dx}(\sin x) = \cos x
   • \frac{d}{dx}(x) = 1
3. Substitute back: \lim_{x \to 0} \frac{\cos x}{1} = \cos 0 = 1.
4. Therefore, \lim_{x \to 0} \frac{\sin x}{x} = 1.

Practice Problem (Try It):

Compute \lim_{x \to 0} \frac{1 - \cos x}{x^2} using L’Hôpital’s Rule. Solution: \lim_{x \to 0} \frac{1 - \cos x}{x^2}=\frac{1}{2}.

Limits of Piecewise Functions

Piecewise functions often appear in AP® Calculus, especially when analyzing different behaviors on intervals. A piecewise function defines one expression for a certain range of x-values and another expression for a different range.

Evaluating Limits of Piecewise Functions

To find the limit at boundary points, it is important to consider both the left-hand and right-hand limits. If these two one-sided limits match, the overall limit exists. If they do not match, the limit does not exist. Therefore, careful handling of boundaries is a crucial step in any “limits of piecewise functions” exercise.

Example: Limit at a Boundary

Let f(x) = \begin{cases}x^2 - 1 & \text{if } x < 2 \\ x + 3 & \text{if } x \ge 2\end{cases}

Evaluate \lim_{x \to 2} f(x).

Step-by-Step Solution:

1. Find the left-hand limit: \lim_{x \to 2^-} (x^2 - 1) = 2^2 - 1 = 3.
2. Find the right-hand limit: \lim_{x \to 2^+} (x + 3) = 2 + 3 = 5.
3. Compare the two results.
4. Notice that 3 \neq 5, so the left-hand and right-hand limits do not match.
5. Therefore, \lim_{x \to 2} f(x) does not exist.

Common Pitfalls and Troubleshooting

Misclassification of the Limit

Sometimes, students assume that direct substitution always works. However, indeterminate forms like \frac{0}{0} should alert you to try factoring or L’Hôpital’s Rule. In addition, always confirm that the function is continuous at the point of interest. If there is a discontinuity, the limit may still exist, but extra steps will be needed.

Algebraic Slips

Algebra mistakes, such as factoring errors or cancelling terms incorrectly, are easy to make. Therefore, double-check each step when simplifying. For instance, watch out for sign changes in the numerator or denominator. Correct classification and careful algebraic manipulation reduce the risk of such slips.

Quick Reference Chart: Vocabulary and Definitions

Term	Definition/Explanation
Limit	The value a function approaches as the input (x) approaches a certain number.
Direct Substitution	A method to evaluate a limit by directly replacing x with the point of interest.
Indeterminate Form	A form like 0/0 or ∞/∞ that requires special techniques beyond direct substitution.
L’Hôpital’s Rule	A rule stating that if a limit yields 0/0 or ∞/∞, one may take derivatives of numerator and denominator.
Piecewise Function	A function defined by different expressions depending on the interval of x.

Conclusion

The mastery of limits sets the stage for a deeper understanding of calculus. Techniques such as direct substitution, factoring, and L’Hôpital’s Rule provide the tools needed to handle a wide range of problems, including limits of piecewise functions. In addition, consistent calculus limits practice is the best way to gain confidence and speed.

Ultimately, limits reappear in almost every major topic in calculus, including derivatives and integrals. Therefore, practicing these skills now will make future lessons more approachable. Keep reviewing and refining these methods to ensure success in AP® Calculus AB-BC and beyond.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.