What We Review
Introduction
Continuity plays a key role in AP® Calculus AB-BC. It refers to the idea that a function has no breaks, jumps, or gaps at a particular point. In other words, a continuous function can be traced without ever lifting a pen. The limit definition of continuity is essential to grasp this concept, making it crucial to understand before exploring advanced calculus topics.
This post will explain what continuity means, why it matters, and how the limit definition of continuity forms its foundation. It will also describe how continuity vs discontinuity differ and highlight a few common types of discontinuities. Finally, there will be a quick reference chart for handy review.
What Is Continuity?
Intuitive Understanding of Continuity
Everyday life often features processes that run smoothly, such as a water faucet flowing without any pauses. These events can be compared to continuous functions: there is no sudden break, so they proceed as expected. In mathematics, a function is continuous at a point if it behaves like a smooth, uninterrupted stream of values at that point.
The key takeaway is that a function is considered continuous if it has no breaks, gaps, or sudden jumps at a given location.
Introductory Example
Consider the function f(x) = 2x + 3. Check continuity at x = 2 using a simple approach.
Step-by-Step Solution
- State the function: f(x) = 2x + 3.
- Evaluate the function at x = 2:f(2) = 2(2) + 3 = 4 + 3 = 7.
- Find the limit of f(x) as x \to 2: Because f(x) = 2x + 3 is a polynomial, its limit at x = 2 is the same as its value at x = 2. Thus, \lim_{x \to 2} f(x) = 7.
- Compare the limit to the function value: \lim_{x \to 2} f(x) = f(2) = 7.
Therefore, the function is continuous at x = 2 because the limit value matches the actual function value.
Formal Limit Definition of Continuity
Three Conditions for Continuity at x = c
The formal limit definition of continuity states that a function f(x) is continuous at x = c if:
- f(c) must exist.
- \lim_{x \to c} f(x) must exist.
- \lim_{x \to c} f(x) = f(c).
These three conditions ensure there are no surprises at the point x = c.
Detailed Explanation of Each Condition
- The function value f(c) must be defined. A function cannot be continuous where it does not exist.
- The limit \lim_{x \to c} f(x) must exist, meaning the function settles to a single value as x gets closer to c from both sides.
- Finally, the limit must match the function’s actual value. If these two values are not the same, the function cannot be continuous at x = c.
Example with Step-by-Step Solution
Consider the piecewise function: f(x) =\begin{cases}x^2 & \text{if } x \neq 3 \\ 9 & \text{if } x = 3.\end{cases}
Examine continuity at x = 3.
- Does f(3) exist? Yes, by the definition of the function, f(3) = 9.
- What is \lim_{x \to 3} f(x)? For x \neq 3, f(x) = x^2. As x \to 3, x^2 \to 9. So, \lim_{x \to 3} f(x) = 9.
- Compare the limit to the function value: \lim_{x \to 3} f(x) = 9, and f(3) = 9. These match.
Therefore, the three conditions are satisfied at x = 3, making f(x) continuous there according to the limit definition of continuity.
Continuity vs Discontinuity
Sometimes, a function does not behave smoothly. Thus, it is important to understand continuity vs discontinuity. Discontinuities occur if any of the three conditions for continuity are not met.
Types of Discontinuities
- Removable Discontinuity: Often happens when there is a “hole” in the function.
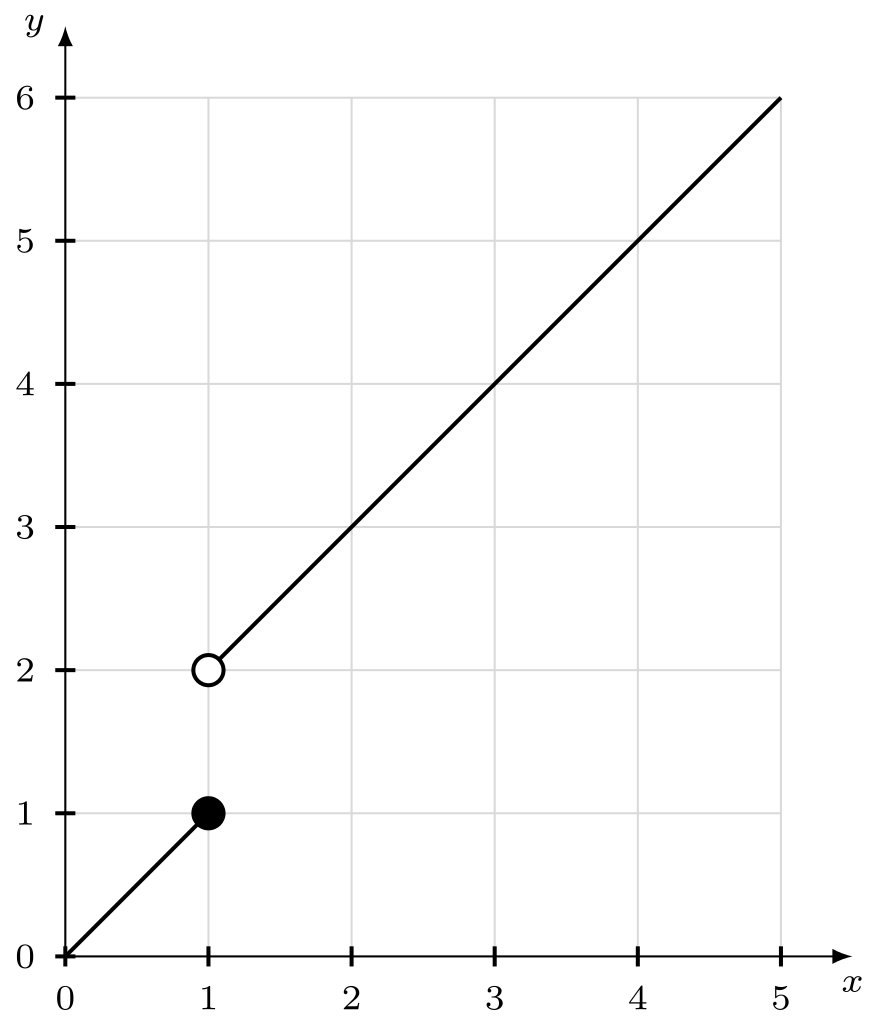
- Jump Discontinuity: The left limit and the right limit as x approaches a point do not match. The image below is a standard example of a jump discontinuity.
- Infinite Discontinuity: The function grows without bound near a certain point, so the limit does not exist in a finite sense.
Why Discontinuities Matter
Discontinuities can create problems in real-world settings. For instance, a function that models supply and demand might show a jump discontinuity if a resource suddenly disappears. Knowing where a function is continuous or discontinuous helps when applying advanced theorems in AP® Calculus AB-BC.
Quick Reference Chart
| Term | Definition |
| Continuity | A function f is continuous at x = c if f(c) is defined, the limit as x \to c exists, and both are equal. |
| Discontinuity | A point where a function is not continuous, potentially due to a hole, jump, or vertical asymptote. |
| Limit Definition of Continuity (at x = c) | The formal requirement that f(c) exists, the limit \lim_{x \to c} f(x) exists, and they are the same. |
| Removable Discontinuity | A “hole” in the function where the limit exists but the function value is either not defined or different. |
| Jump Discontinuity | Occurs when the left and right limits differ, creating a sudden jump in function values. |
| Infinite Discontinuity | Happens if the function value grows without bound near a certain point, causing the limit to fail to exist. |
Conclusion
The limit definition of continuity offers a precise way to check whether a function is continuous at a point. It ensures that the function value exists, the limit exists, and both are in perfect agreement. This framework clarifies what continuity is and how functions can either be seamless or experience discontinuities.
By understanding continuity vs discontinuity now, it becomes easier to explore the Intermediate Value Theorem, differentiability, and other important ideas in AP® Calculus AB-BC. Transitioning with confidence to deeper concepts is much smoother after mastering these foundational principles of continuity.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








