Infinite limits are a fascinating topic in calculus, especially when exploring the behavior of functions near certain critical values. They appear when a function grows larger and larger—or smaller and smaller—without bound. In AP® Calculus AB-BC 1.14 infinite limits and vertical asymptotes (LIM-2.D.1, LIM-2.D.2), understanding these concepts is key for deeper analysis. Therefore, learning how to determine infinite limits is crucial.
Infinite limits help us understand the behavior of functions in extreme circumstances. They also connect directly to the idea of vertical asymptotes, where a function keeps shooting up or down infinitely near some x-value. Mastering these ideas allows for a more thorough exploration of advanced calculus problems.
What We Review
What Are Infinite Limits?
Defining Infinite Limits
An infinite limit occurs when a function f(x) approaches positive or negative infinity as x moves closer to a particular value. In other words, there is no real number that the function settles on; instead, the function’s outputs keep growing in magnitude.
For instance, consider \lim_{x \to 0^+} f(x) = \infty. This record means the function grows positively without bound as x approaches 0 from the right. If it grows in the negative direction, we might see \lim_{x \to 0^-} f(x) = -\infty. Both scenarios indicate the function does not reach a specific finite value. The scenario described can be seen in the image below:
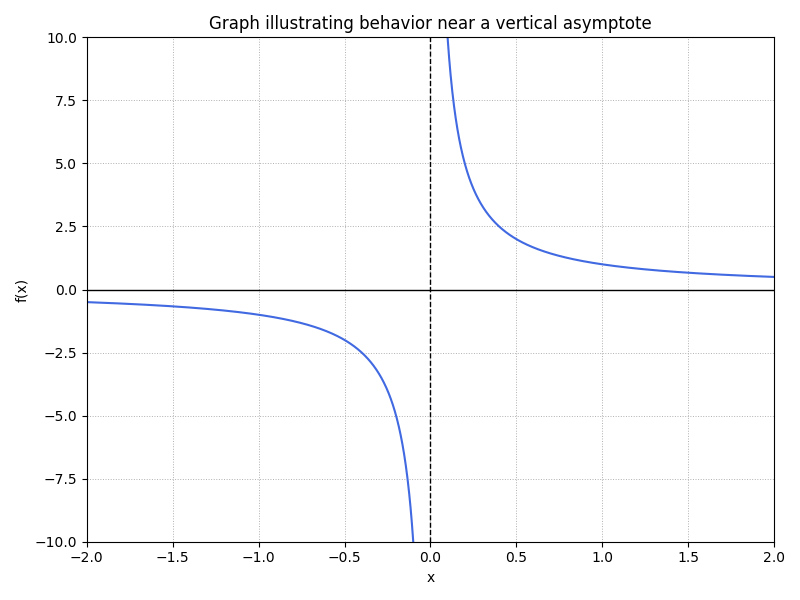
Key Points to Remember
- Positive infinity: The function’s values become larger and larger without limit.
- Negative infinity: The function’s values become more and more negative without limit.
- If the denominator moves toward zero while the numerator stays nonzero, the function often explodes to infinity (positive or negative, depending on signs).
Example with Step-by-Step Solution
Consider the function f(x) = \frac{1}{x - 2} and evaluate \lim_{x \to 2} f(x):
- Substitute x = 2 into f(x): \frac{1}{2-2} = \frac{1}{0}, which is undefined.
- Analyze the behavior as x approaches 2 from the left (x \to 2^-) and from the right (x \to 2^+):
- When x is just less than 2, x - 2 is negative and very small. Thus, \frac{1}{x - 2} is a large negative value, heading toward negative infinity.
- When x is just greater than 2, x - 2 is positive and very small. Therefore, \frac{1}{x - 2} is a large positive value, heading toward positive infinity.
- Conclude that \lim_{x \to 2^-} f(x) = -\infty and \lim_{x \to 2^+} f(x) = \infty. The limit does not exist as a single finite number, but each one-sided limit goes off to infinity (with different signs).
How to Determine Infinite Limits
Recognizing When a Function Might Approach Infinity
Sometimes a function might appear to explode to infinity near specific points. Therefore, take note of these signs:
- A denominator moving to zero while the numerator remains nonzero.
- Polynomial or exponential terms in the numerator or denominator that outpace everything else.
- Expressions involving repeated multiplication or exponentials that enlarge values as x grows.
Algebraic Tools and Techniques
To find out how to determine infinite limits, keep these techniques in mind:
- Factor and simplify expressions if possible.
- Identify any dominant terms in a polynomial.
- Divide numerator and denominator by the highest power of x found, especially for limits at \pm \infty.
Example with Step-by-Step Solution
Evaluate the limit \lim_{x \to 1} \frac{x^2 - 1}{x - 1}:
- Setup: Notice that direct substitution of x = 1 gives \frac{0}{0}, which is an indeterminate form.
- Factor and simplify the expression: x^2 - 1 = (x - 1)(x + 1), so \frac{x^2 - 1}{x - 1} = \frac{(x - 1)(x + 1)}{x - 1}.
- Cancel out the common factor x - 1: This simplifies to x + 1, as long as x \neq 1.
- Determine behavior as x approaches 1: Now \lim_{x \to 1} (x + 1) = 2. However, this example does not have an infinite limit after simplification. If the simplified result had caused the function to blow up near x = 1, that would suggest an infinite limit.
Practice Problem with Infinite Limit: Try evaluating \lim_{x \to 3} \frac{6}{(x-3)}. Follow similar steps:
- Substitute x = 3.
- Notice the denominator approaches zero.
- Check the sign of the denominator on each side of 3. Does it go to positive or negative infinity?
Solution: \lim_{x \to 3} \frac{6}{(x-3)} does not exist. It approaches infinity from the right and negative infinity from the left.
Vertical Asymptotes
Definition of a Vertical Asymptote
A vertical asymptote is a vertical line (for example, x = a) where the function’s value grows larger or smaller without bound, indicating an infinite limit in the positive or negative direction. Thus, vertical asymptotes are tied closely to infinite limits.
Finding Vertical Asymptotes
The most common way to spot a vertical asymptote is:
- Identify values of x that make the denominator zero.
- Check that the numerator does not also become zero at these values (which might cancel out the issue).
- Finally, see if the function really tends to \pm \infty as x nears those points.
Example with Step-by-Step Solution
Find any vertical asymptotes of g(x) = \frac{2x}{x - 4}:
- Setup: Look for x that makes the denominator zero. Here, x - 4 = 0 implies x = 4.
- Verify that the numerator is not zero at the same point: At x = 4, the numerator is 2(4) = 8 \neq 0.
- Observe the behavior near x = 4: As x \to 4, the denominator becomes tiny, so the fraction’s magnitude becomes very large (positive or negative, depending on the side).
- Conclusion: x = 4 is a vertical asymptote because \lim_{x \to 4} g(x) goes off to infinity or negative infinity, depending on the direction.
Quick Reference Chart: Important Vocabulary and Definitions
| Term | Definition/Explanation |
| Infinite Limit | A limit in which the function grows without bound (positive or negative) as x approaches a specific value. |
| Vertical Asymptote | A vertical line x = a where the function tends to ±∞ as x approaches a. |
| Unbounded Behavior | Occurs when the function’s output grows larger and larger in the positive or negative direction and does not settle. |
| Denominator Tending to Zero | Often a key indicator that correlates with infinite limits, as the function’s value might blow up to ±∞. |
| Dominant Term | The term in a polynomial or expression that grows fastest for large values of x. |
Conclusion
Infinite limits capture the essence of boundless growth and are a crucial tool in understanding more complex calculus topics. They directly connect to vertical asymptotes, where functions stretch to infinity near specific x-values. Therefore, to master 1.14 infinite limits and vertical asymptotes, it is vital to identify when the denominator goes to zero, factor to uncover hidden behavior, and watch how dominant terms drive the function’s growth.
Learning how to determine infinite limits helps in tackling rigorous problems in AP® Calculus and beyond. These concepts reappear in areas like infinite series, integrals, and advanced real analysis. By following the steps laid out here, students can gain confidence and build a stronger calculus foundation.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








