The difference quotient formula helps measure how much a function changes over a small interval. It is a powerful concept because it lays the groundwork for understanding derivatives. In simpler terms, the difference quotient formula represents the average rate of change of a function over a chosen step, often called “h.” This approach appears in the AP® Calculus AB-BC curriculum, where students learn to move from average rates of change to instantaneous rates of change.
This transition is crucial because it bridges basic algebraic ideas with advanced calculus. By mastering how to find difference quotient values, students can see how small changes in input affect the output. In the next sections, each step of the difference quotient formula is broken down into manageable parts.
What We Review
Difference Quotient Formula Explained
Definition and Purpose
The difference quotient formula is usually written as: \frac{f(a + h) - f(a)}{h}
It calculates the average rate of change of a function f(x) between two points on the function’s curve: at x = a and x = a + h. Thus, it shows how much the function’s output changes when the input shifts by a small amount h. Therefore, grasping how to find difference quotient values is a key step toward understanding the foundation of derivatives.
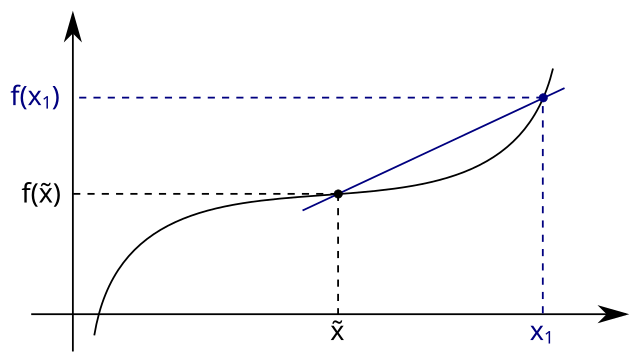
In practice, the difference quotient formula provides a way to see how a function behaves. By examining the change over an interval, one can later explore what happens as h \to 0 to find instantaneous rates of change, known as derivatives. The image below illustrates the average rate of change of a function over an interval by connecting a line through two points on the function’s graph.
Example: Calculating a Basic Difference Quotient
Consider the simple polynomial function f(x) = x^2. Follow these steps to compute the difference quotient at x = a:
- Write down the formula: \frac{f(a + h) - f(a)}{h}
- Substitute f(x) = x^2 into the expression: f(a + h) = (a + h)^2 = a^2 + 2ah + h^2.
- Compute the numerator: f(a + h) - f(a) = (a^2 + 2ah + h^2) - a^2 = 2ah + h^2.
- Divide by h: \frac{2ah + h^2}{h} = 2a + h.
Hence, the difference quotient for f(x) = x^2 at the point x = a is 2a + h. This expression is quite useful because if h becomes very small, it approaches 2a, which is closely related to the function’s derivative at that point.
Average Rate of Change vs. Instantaneous Rate of Change
From the Difference Quotient to the Limit
The difference quotient formula measures the average rate of change between two points. However, by taking the limit of difference quotient as h \to 0, the result reveals the instantaneous rate of change at a point. This result is called the derivative.
Formally, the derivative at x = a is: \lim_{h \to 0} \frac{f(a + h) - f(a)}{h}
In other words, focusing on ever-smaller intervals gives a deeper insight into the function’s behavior at a specific point in time. Therefore, the limit concept transforms “average” rates of change into something that shows how the function changes at a single moment.
Example: Transitioning to the Derivative at a Specific Point
Let f(x) = 3x + 2. Use the difference quotient to find the derivative at a point x = a:
- Write the difference quotient: \frac{f(a + h) - f(a)}{h}.
- Find f(a + h): f(a + h) = 3(a + h) + 2 = 3a + 3h + 2.
- Subtract f(a): f(a + h) - f(a) = (3a + 3h + 2) - (3a + 2) = 3h.
- Divide by h and simplify: \frac{3h}{h} = 3.
- Take the limit as h \to 0: \lim_{h \to 0} 3 = 3.
Thus, the derivative at a point is 3 for this linear function. This shows that the instantaneous rate of change is constant everywhere, which makes sense for a linear function.
Why the Difference Quotient Matters in Calculus
Link to Derivative at a Point
The derivative at a point is a core idea in calculus. It measures how fast a function increases or decreases at a single value of x. Because derivatives come from taking the limit of difference quotient expressions, it is helpful for students to master the difference quotient formula early on.
Consequently, many real-world applications depend on this understanding. For instance, velocity can be viewed as the derivative of position, and acceleration is the derivative of velocity. By connecting these ideas, the difference quotient formula provides a stepping stone toward advanced topics.
Example: Using the Difference Quotient for a Real-Value Function
Imagine a function f(x) = x^2 + 4x, which might represent temperature changes over time. Suppose one is curious about how quickly temperature changes at x = 2. Follow these steps to find the instantaneous rate of change using the difference quotient:
- Write f(a + h) when a = 2: f(2 + h) = (2 + h)^2 + 4(2 + h) = 4 + 4h + h^2 + 8 + 4h = h^2 + 8h + 12.
- Compute the numerator of the difference quotient: f(2 + h) - f(2). First, find f(2) = 2^2 + 4(2) = 4 + 8 = 12. Therefore:f(2 + h) - f(2) = (h^2 + 8h + 12) - 12 = h^2 + 8h.
- Divide by h: \frac{h^2 + 8h}{h} = h + 8.
- Observe what happens as h \to 0: \lim_{h \to 0} (h + 8) = 8.
Hence, the derivative at x = 2 is 8. In a temperature context, this means the rate of change is 8 units per one unit of time at precisely x = 2.
Quick Reference Chart: Important Vocabulary and Definitions
| Term | Definition |
| Difference Quotient | \frac{f(a+h) - f(a)}{h}, a formula measuring average rate of change over h. |
| Average Rate of Change | The amount a function’s output changes per unit increase in its input over a specific interval. |
| Instantaneous Rate of Change | The rate of change at a single point, found using derivatives. |
| Derivative at a Point | The limit of difference quotient as h \to 0, giving the exact rate of change. |
| Limit of Difference Quotient | \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}, a process defining the derivative. |
Conclusion
The difference quotient formula connects the idea of average rate of change to the more advanced concept of instantaneous rate of change. By placing h closer to zero, the limit of difference quotient leads directly to the derivative at a point. This step is essential for deeper calculus applications such as velocity, acceleration, and other real-world scenarios.
Developing skill in working with the difference quotient formula enables students to understand core topics in calculus with more clarity and confidence. Once the difference quotient is second nature, finding derivatives becomes more intuitive, paving the way for success in AP® Calculus and beyond.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 1.16 Working with the Intermediate Value Theorem (IVT)
- 2.2 Defining the Derivative of a Function and Using Derivative Notation
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








