Derivatives are a central part of calculus, measuring how functions change with respect to their inputs. Learning the basics of derivatives sets the stage for more advanced topics like optimization and related rates. In this article, we’ll cover a basic rule: the power rule for derivatives.
However, the process of finding derivatives from scratch using the limit definition can be time-consuming. That’s where the power rule for derivatives comes in. This simple formula applies to functions of the form x^r and significantly reduces the work needed. The “power rule for derivatives” is often the first shortcut introduced in calculus classes.
What We Review
Understanding the Power Rule
Statement of the Rule
For any real number r, if f(x) = x^r, then its derivative can be found with:
\frac{d}{dx}\big[x^r\big] = r \cdot x^{r-1} .This rule applies to all real exponents, including negative and fractional values. Therefore, “power rule calculus” can be used in a wide variety of problems, making it very versatile.
Why It Works
While the power rule is often memorized, it comes from the limit definition of the derivative:
f'(x) = \lim_{h \to 0} \frac{(x + h)^r - x^r}{h}.Through expanding and simplifying, the terms cancel out so that the result is r \cdot x^{r-1}. Although the full expansion can be lengthy, the core takeaway is that the limit definition supports this handy shortcut.
Examples with Step-by-Step Solutions
Derivative of a Basic Positive Integer Power
Consider the function f(x) = x^3. Find f'(x).
- Identify the exponent: r = 3.
- Apply the power rule: \frac{d}{dx}\big[x^3\big] = 3 \cdot x^{3-1}.
- Simplify the expression: 3 \cdot x^2.
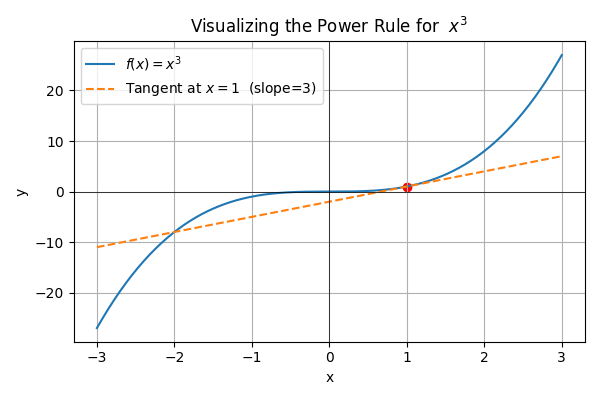
Therefore, f'(x) = 3x^2. The image below shows the value of the slope at x=1 .
Try a quick practice on f(x) = x^4. Applying the same steps yields f'(x) = 4x^3.
Derivative of √x (Fractional Exponent)
The expression \sqrt{x} can be rewritten as x^{\frac{1}{2}}. To find the “derivative of sqrt x,” use the power rule with r = \tfrac{1}{2}:
- Rewrite \sqrt{x} as x^{\frac{1}{2}}.
- Apply the power rule: \frac{d}{dx}\big[x^{\frac{1}{2}}\big] = \frac{1}{2} \cdot x^{\frac{1}{2}-1}.
- Simplify the exponent: \frac{1}{2} - 1 = -\frac{1}{2}.
- Hence, the derivative is \frac{1}{2}x^{-\frac{1}{2}}.
This can be written as \frac{1}{2\sqrt{x}}, but remembering x^{-\frac{1}{2}} is often more convenient for future steps.
Derivative of 1/x² (Negative Exponent)
Another common function is \frac{1}{x^2}, which can be expressed as x^{-2}. To find the “derivative of 1/x^2,” follow these steps:
- Rewrite \frac{1}{x^2} as x^{-2}.
- Apply the power rule: \frac{d}{dx}\big[x^{-2}\big] = -2 \cdot x^{-3}.
- Keep the negative exponent form or rewrite it. If needed, simplify to -\frac{2}{x^3}.
Both forms are correct, but -2x^{-3} is often easier to use for advanced problems.
Additional Tips and Common Mistakes
Checking Algebraic Simplifications
It is helpful to rewrite functions with fractional or negative exponents before using the power rule. For example, rewriting \sqrt{x} as x^{1/2} ensures simpler calculations. Therefore, always pause to check if changing a radical or fraction into an exponent makes the derivative easier to compute.
After getting the derivative, remember to simplify. Mixed terms like x^3\cdot x^{-1} can be combined. Keeping the expression neat helps in later stages of calculus problems.
Avoiding Minor Errors
A common mistake is forgetting to subtract 1 from the exponent. Carefully track the new exponent, especially with fractions like \frac{1}{2} - 1. Another slip occurs when dealing with negative exponents. Remember that x^{-a} is \frac{1}{x^a}, and the sign of the exponent changes the function’s shape. Properly handling these details consistently leads to accurate answers.
Quick Reference Chart
| Term | Definition |
| Power Rule for Derivatives | If f(x) = x^r, then f'(x) = r \cdot x^{r-1}. |
| Derivative | The rate at which a function changes with respect to its input. |
| Exponent | The power to which a value or expression is raised (e.g., x^3 has exponent 3). |
| Negative Exponent | An exponent that is less than zero, such as x^{-2}. |
| Fractional Exponent | An exponent that is a fraction, such as x^{\frac{1}{2}}. |
Conclusion
The power rule for derivatives is a powerful tool that simplifies the process of finding derivatives of functions with exponents. Through a quick calculation involving multiplying by the original exponent and reducing it by one, many tasks in calculus become more straightforward.
This rule also connects to more complex scenarios in differential calculus. By keeping a clear grasp of exponent manipulation, algebraic simplifications, and a careful approach to each step, students will find the power rule essential for tackling polynomial, radical, and other exponential functions in calculus.
Finally, continued practice with different exponents is key. The power rule’s ability to handle positive, fractional, and negative exponents will prove useful in integration, optimization, and throughout advanced college-level courses.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 2.4 Connecting Differentiability and Continuity: Determining When Derivatives Do and Do Not Exist
- 2.6 Derivative Rules: Constant, Sum, Difference, and Constant Multiple
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








