The derivative quotient rule is an essential technique in AP® Calculus AB-BC. It helps when finding the derivative of a function expressed as one expression divided by another. This concept expands on simpler derivative rules, such as the power rule and product rule. However, it specifically addresses problems where a function sits in the numerator while another function remains in the denominator.
Because divisions often appear in calculus problems, the quotient rule formula is a core tool. Mastering this rule ensures confidence when working with advanced topics and related rates. Therefore, understanding each step of the quotient rule process sets a strong foundation for future calculus success.
What We Review
Understanding the Derivative Quotient Rule Formula
The calculus quotient rule states that if a function h(x) is formed as h(x) = \frac{f(x)}{g(x)}, its derivative takes a particular form. The rule is similar to the product rule, but there is a key difference: it involves a subtraction in the numerator and always includes the square of the denominator in the final result.
Here is the precise quotient rule formula:
\displaystyle h'(x) = \frac{f'(x)g(x) - f(x)g'(x)}{\bigl(g(x)\bigr)^2}This formula might look intimidating at first. However, one can see it as f times the derivative of g minus g times the derivative of f, then all divided by g squared.
Step-by-Step Guide to Using the Derivative Quotient Rule
When applying 2.9 the quotient rule, consider these steps:
- Identify u(x) as the numerator function and v(x) as the denominator function.
- Compute u'(x) and v'(x), the derivatives of the top and bottom functions.
- Plug these results into the quotient rule formula \frac{u'(x),v(x) - u(x),v'(x)}{(v(x))^2}.
- Simplify the expression carefully by distributing and combining like terms if needed.
These steps help maintain a clear process. Moreover, carefully labeling each part is critical for avoiding errors.
Example 1: Simple Function Application
Consider the following function:
y = \frac{2x^2 + 3x}{x + 1}Use the derivative quotient rule to find y'(x).
Step-by-Step Solution
- Let u(x) = 2x^2 + 3x. Then u'(x) = 4x + 3.
- Let v(x) = x + 1. Then v'(x) = 1.
- According to the quotient rule formula, \displaystyle y'(x) = \frac{(4x + 3)(x + 1) - (2x^2 + 3x)(1)}{(x + 1)^2}
- Expand the numerator:
- (4x + 3)(x + 1) = 4x^2 + 4x + 3x + 3 = 4x^2 + 7x + 3.
- Subtract (2x^2 + 3x): 4x^2 + 7x + 3 - (2x^2 + 3x) = (4x^2 - 2x^2) + (7x - 3x) + 3 = 2x^2 + 4x + 3.
- Thus, \displaystyle y'(x) = \frac{2x^2 + 4x + 3}{(x + 1)^2}
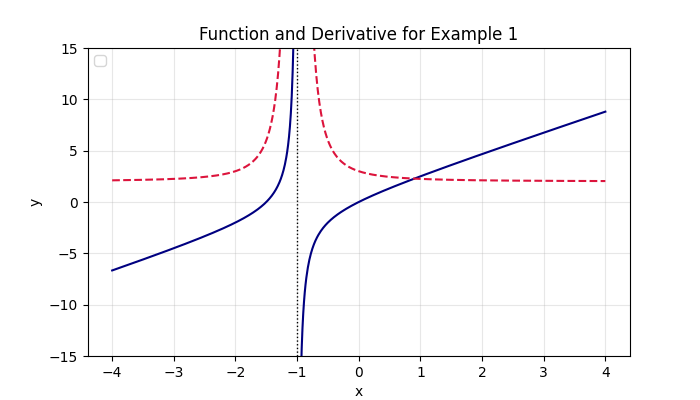
Therefore, the derivative is \frac{2x^2 + 4x + 3}{(x + 1)^2}. Notice how each part fits directly into this pattern, highlighting the power of the calculus quotient rule. The image below shows the function and its derivative graphed in the same viewing window.
Common Mistakes and Tips
- Watch out for negative signs: An easy way to slip up is to forget that the term f(x)g'(x) is subtracted in the numerator.
- Remember to square the denominator: g(x)^2 must be written correctly.
- Simplify the final expression: Combining like terms at the end often reduces confusion in later steps.
- Be systematic: Each term should be carefully substituted, with close attention paid to f'(x) and g'(x) to avoid mixing them up.
Example 2: More Complex Function
Next, examine a more involved function:
y = \frac{3x^3 - x + 2}{2x - 4}Step-by-Step Solution
- Identify the numerator and its derivative:
- u(x) = 3x^3 - x + 2
- u'(x) = 9x^2 - 1
- Identify the denominator and its derivative:
- v(x) = 2x - 4
- v'(x) = 2
- Apply the quotient rule formula: \displaystyle y'(x) = \frac{(9x^2 - 1)(2x - 4) - (3x^3 - x + 2)(2)}{(2x - 4)^2}
- Expand the numerator step by step:
- (9x^2 - 1)(2x - 4) = 18x^3 - 36x^2 - 2x + 4
- (3x^3 - x + 2)(2) = 6x^3 - 2x + 4
- Subtract the second expansion from the first: \displaystyle (18x^3 - 36x^2 - 2x + 4) - (6x^3 - 2x + 4) = (18x^3 - 6x^3) + (-36x^2) + (-2x + 2x) + (4 - 4)
- This simplifies to 12x^3 - 36x^2.
- Hence, \displaystyle y'(x) = \frac{12x^3 - 36x^2}{(2x - 4)^2}
One could factor out common terms, but leaving it as \frac{12x^3 - 36x^2}{(2x - 4)^2} is valid. However, simplifying might make further calculations easier.
Quick Reference Chart
| Term | Definition |
| Quotient Rule | The formula \frac{u'(x)v(x) - u(x)v'(x)}{(v(x))^2} for finding the derivative of a fraction of two functions. |
| Numerator | The top function (u) in a rational expression. |
| Denominator | The bottom function (v) in a rational expression. |
| Derivative | The slope of a function or rate of change of a function at any given point. |
Conclusion
The derivative quotient rule is more than just another tool; it is the direct response to handling divisions in an efficient way. Moreover, 2.9 the quotient rule bridges earlier derivative principles with more sophisticated calculus concepts. By recalling the difference in the numerator and the squared denominator, students can systematically solve advanced derivative problems. Therefore, remembering each step matters, especially as functions become increasingly complex. Mastering the quotient rule formula ensures readiness for higher-level topics in calculus and beyond.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








