What We Review
Introduction
Implicit differentiation appears regularly in AP® Calculus AB and BC. It provides a method for finding the derivative without solving for y explicitly. This concept links closely to the chain rule mentioned in FUN-3.D.1, which states that each time y appears in a function, it should be treated as a function of x. Therefore, implicit differentiation becomes a key tool when equations are difficult or impossible to rearrange into y = f(x). This article simplifies the idea with worked examples and a quick reference chart.
What Is Implicit Differentiation?
Implicit differentiation is a process for finding dy/dx when y is not isolated on one side of the equation. In other words, it handles situations where x and y are intermixed. For instance, the equation x^2 + y^2 = 25 does not say y is some explicit function of x. However, calculus still allows the calculation of the derivative of y with respect to x. This method is essential when performing advanced tasks in AP® Calculus, such as related rates and curve sketching.
The Rules of Implicit Differentiation
A) Recognizing Functions Written Implicitly
Some equations are written in a way that does not separate y. These forms are called implicit equations. By contrast, explicit equations isolate y, such as y = x^2. However, implicit equations might look like x^2 + xy + y^2 = 12. In such cases, y is still a function of x, even if it is not obvious. Therefore, it is crucial to remember that y depends on x throughout the differentiation process.
B) Applying the Chain Rule
Fun-3.D.1 highlights the importance of the chain rule, which states: \frac{d}{dx} \bigl(f(g(x))\bigr) = f'(g(x)) \cdot g'(x). When there is a term involving y, treat y as a function of x. Therefore, any time y appears, multiply by dy/dx to represent the hidden chain rule step. For example, differentiating y^2 with respect to x results in 2y \cdot \frac{dy}{dx}.
C) Collecting dy/dx Terms
After applying the chain rule to every term, collect the dy/dx pieces on one side of the equation. Then, factor out dy/dx. Finally, solve for dy/dx by isolating it. This step-by-step approach ensures clarity when working through the problem.
Example 1: Basic Implicit Differentiation Step-by-Step
Consider the equation xy = 1. This is an implicit equation because y is mixed with x.
- Write the given equation: xy = 1
- Differentiate both sides with respect to x.
- Differentiate x \cdot y as a product: \frac{d}{dx}(xy) = \frac{dx}{dx} \cdot y + x \cdot \frac{dy}{dx}. Notice that \frac{dx}{dx} = 1 and \frac{d}{dx}(y) = \frac{dy}{dx}.
- Differentiate the right side: \frac{d}{dx}(1) = 0.
- Rewrite with the chain rule included: 1 \cdot y + x \cdot \frac{dy}{dx} = 0.
- Isolate dy/dx: y + x \cdot \frac{dy}{dx} = 0. Therefore, x \cdot \frac{dy}{dx} = -y. Hence, \frac{dy}{dx} = -\frac{y}{x}.
Practice Problem for Example 1
Differentiate the equation x^2 + xy = 6 implicitly and find dy/dx.
Step-by-Step Solution:
- Start with: x^2 + xy = 6.
- Differentiate both sides:
- \frac{d}{dx}(x^2) = 2x.
- \frac{d}{dx}(xy) = x \frac{dy}{dx} + y \cdot 1.
- \frac{d}{dx}(6) = 0.
- Combine results: 2x + \bigl(x \frac{dy}{dx} + y\bigr) = 0.
- Rewrite: 2x + x \frac{dy}{dx} + y = 0.
- Collect dy/dx terms: x \frac{dy}{dx} = -2x - y.
- Solve for dy/dx: \frac{dy}{dx} = -\frac{2x + y}{x}.
Example 2: Slightly More Complex Implicit Differentiation
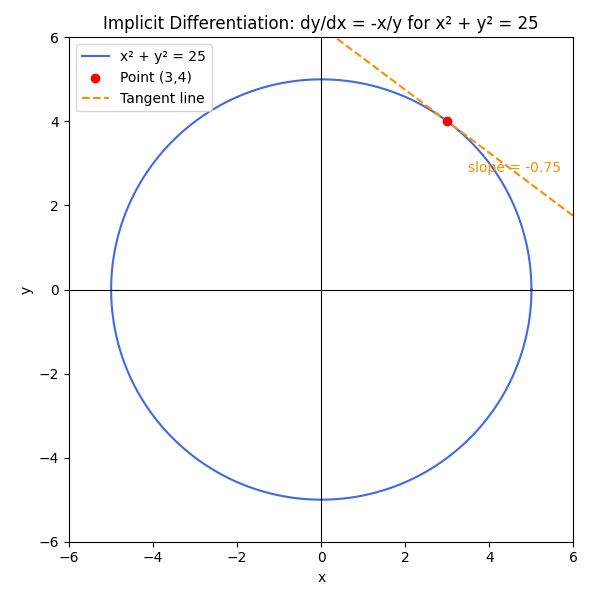
Consider x^2 + y^2 = 25. This equation represents a circle, but the focus is on applying implicit differentiation carefully.
- Write the equation: x^2 + y^2 = 25.
- Differentiate the left side:
- \frac{d}{dx}(x^2) = 2x.
- \frac{d}{dx}(y^2) = 2y \cdot \frac{dy}{dx} (using the chain rule).
- Differentiate the right side:
- \frac{d}{dx}(25) = 0.
- Combine everything: 2x + 2y \cdot \frac{dy}{dx} = 0.
- Factor out and solve for dy/dx: 2y \cdot \frac{dy}{dx} = -2x. Hence, \frac{dy}{dx} = -\frac{x}{y}.
The image below illustrates the slope at the point (3,4) using this solution.
Practice Problem for Example 2
Differentiate x^3 + xy + y^3 = 12 and solve for dy/dx.
Step-by-Step Solution
- Start with: x^3 + xy + y^3 = 12.
- Differentiate term by term:
- \frac{d}{dx}(x^3) = 3x^2.
- \frac{d}{dx}(xy) = x \frac{dy}{dx} + y(1).
- \frac{d}{dx}(y^3) = 3y^2 \cdot \frac{dy}{dx}.
- \frac{d}{dx}(12) = 0.
- Combine results: 3x^2 + x \frac{dy}{dx} + y + 3y^2 \cdot \frac{dy}{dx} = 0.
- Group dy/dx terms: x \frac{dy}{dx} + 3y^2 \frac{dy}{dx} + 3x^2 + y = 0.
- Factor out dy/dx: (x + 3y^2)\frac{dy}{dx} + 3x^2 + y = 0.
- Solve for dy/dx: (x + 3y^2)\frac{dy}{dx} = -3x^2 - y. Therefore, \frac{dy}{dx} = -\frac{3x^2 + y}{x + 3y^2}.
Common Mistakes and How to Avoid Them
- Forgetting that y depends on x, thus missing a factor of dy/dx.
- Not applying the product rule when x and y appear together as a multiplied term.
- Mixing up negative signs and constants. Therefore, it is wise to differentiate slowly, checking each term carefully. Additionally, it helps to confirm that every term with y includes dy/dx.
Quick Reference Chart (Vocabulary & Definitions)
| Term | Definition/Explanation |
| Implicit Differentiation | Technique for finding dy/dx when y is not isolated as in y = f(x). |
| Explicit Form | Equation where y is explicitly written in terms of x, such as y = x^2 + 3. |
| Chain Rule | Fundamental rule stating \frac{d}{dx}(f(g(x))) = f'(g(x)) \cdot g'(x). |
| dy/dx | Symbol representing the derivative of y with respect to x. |
| Rules of Implicit Differentiation | Steps involving the chain rule, collecting dy/dx terms, and isolating the derivative. |
Conclusion
Implicit differentiation is a powerful skill in AP® Calculus AB and BC. It simplifies finding the derivative when an equation cannot be rearranged into an explicit form. Therefore, practice using the chain rule and collecting dy/dx carefully. By mastering the rules of implicit differentiation, students prepare themselves for complex calculus applications such as related rates and higher-order rules. Regular study of example-based methods helps build confidence and leads to success on challenging exam questions.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








