Understanding increasing and decreasing intervals is crucial for success in AP® Calculus AB-BC. These intervals reveal where a function’s output is rising or falling, and they connect directly to the concept of a function’s slope. Therefore, they are essential for analyzing real-world trends and changing rates.
In the AP® Calculus AB-BC course description, FUN-4.A.1 highlights the use of the first derivative to determine intervals of increase or decrease. By identifying where the derivative is positive or negative, it becomes easier to interpret a function’s behavior. This article explains the steps, common mistakes, and helpful tips needed to master increasing and decreasing intervals on the AP® exam.
What We Review
Key Concepts: The Derivative and Its Sign
The derivative is the measure of a function’s slope at any given point. In other words, it determines how fast the function changes. It is often written as f'(x) or \frac{d}{dx}.
- A positive derivative implies the function is moving upward, so the function is increasing.
- A negative derivative implies the function is moving downward, so the function is decreasing.
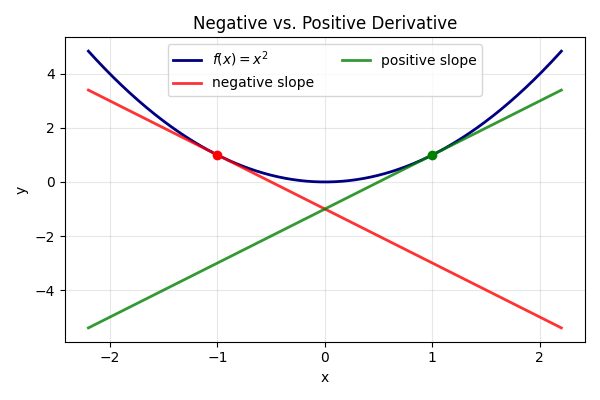
Critical points occur where the derivative is zero or undefined. These points often mark the boundary between increasing and decreasing intervals. However, it is necessary to test intervals around each critical point, rather than assuming zero means automatically changing from increasing to decreasing or vice versa.
Determining Where a Function Is Increasing
General Steps
- Find the derivative of the given function f'(x).
- Identify all values where f'(x) = 0 or f'(x) is undefined; these are critical points.
- Make a sign chart or use a sign test on each interval defined by these critical points.
- If f'(x) > 0 on an interval, then the function is increasing there.
Example and Step-by-Step Solution
Consider the function f(x) = x^3 - 3x^2 + 4.
- Find the derivative: f'(x) = 3x^2 - 6x.
- Identify critical points by setting f'(x) = 0: 3x^2 - 6x = 0 \rightarrow3x(x - 2) = 0. Solutions are x = 0 and x = 2.
- Split the real line into intervals based on the critical points: (-∞, 0), (0, 2), and (2, ∞).
- Test the sign of f'(x) in each interval (pick any test value within each interval).
- For x \in (-∞, 0), pick x = -1: f'(-1) = 3(-1)^2 - 6(-1) = 3 + 6 = 9, which is positive.
- For x \in (0, 2), pick x = 1: f'(1) = 3(1)^2 - 6(1) = 3 - 6 = -3, which is negative.
- For x \in (2, ∞), pick x = 3: f'(3) = 3(3)^2 - 6(3) = 27 - 18 = 9, which is positive.
- Conclude the increasing intervals: f'(x) is positive on (-∞, 0) and (2, ∞). Therefore, f(x) is increasing on those intervals.
Determining Where a Function Is Decreasing
General Steps
- Use the critical points found by setting the derivative to zero or locating undefined points.
- Examine the sign of the derivative in each interval again.
- If f'(x)< 0, the function is decreasing on that interval.
Example and Step-by-Step Solution
Consider h(x) = 2x^2 - 8x + 3.
- Find the derivative: h'(x) = 4x - 8.
- Set h'(x) = 0 to find critical points: 4x - 8 = 0 \implies 4x = 8 \implies x = 2.
- This single critical point, x = 2, divides the real line into two intervals: (-∞, 2) and (2, ∞).
- Test values in each interval to check the derivative’s sign:
- For x \in (-∞, 2), pick x = 0: h'(0) = 4(0) - 8 = -8, which is negative.
- For x \in (2, ∞), pick x = 3: h'(3) = 4(3) - 8 = 12 - 8 = 4, which is positive.
- Conclude the decreasing interval: h'(x) is negative on (-∞, 2). Therefore, h(x) is decreasing on that interval.
Common Mistakes and Helpful Tips
- Mistaking a zero derivative for guaranteed increase or decrease. It is necessary to test intervals on either side of the critical point.
- Forgetting to check for points where the derivative is undefined, especially in rational or trigonometric functions.
- Skipping the sign chart or sign test can lead to incorrect conclusions.
- For efficient calculation, try to simplify the derivative before testing. Also, organize each interval test in a neat list.
- Use derivative rules, such as the product or chain rule, to handle more complicated functions.
Quick Reference Chart (Vocabulary & Definitions)
| Term | Definition |
| Function | A rule that assigns each input to exactly one output. |
| Derivative | The slope of a function at a given point; written as f'(x). |
| Critical Point | A point x where the derivative is zero or undefined. |
| Increasing Interval | Where f'(x) > 0, meaning the function rises as x increases. |
| Decreasing Interval | Where f'(x) < 0, meaning the function falls as x increases. |
Conclusion
Determining increasing and decreasing intervals is straightforward once the derivative is understood. The first derivative indicates where the function’s slope is positive or negative. By finding critical points, creating a sign chart, and confirming the sign of f'(x) in each interval, it becomes clear where a function is rising or falling.
Solidifying these skills is important for AP® Calculus AB-BC success. Since the slope behavior often guides other decisions—such as locating maximums or minimums—understanding increasing and decreasing intervals will help in deeper problem-solving tasks.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.
