The first derivative test is a valuable tool in calculus. It helps determine when a function has local maxima or local minima, often called local extrema or relative extrema. In many AP® Calculus courses, including 5.4 the first derivative test, students learn to apply this concept to various functions. This article explains what the first derivative test is, why it matters, and how to find relative extrema effectively. By the end, the steps for analyzing critical points and classifying maxima or minima should become clearer and more approachable.
What We Review
What Is the First Derivative Test?
Definition and Significance
A first derivative test involves examining the sign of the derivative around critical points. When the derivative switches from positive to negative, that point is a local maximum. Conversely, if the derivative changes from negative to positive, there is a local minimum. Therefore, this is an essential procedure in determining local extrema.
In simpler terms, consider a function f(x). Its first derivative, f'(x), tells whether f(x) is increasing or decreasing within particular intervals. Consequently, a local maximum occurs at a point where the function stops rising and begins falling. A local minimum appears at a point where the function stops falling and begins rising.
Conditions for Applying the First Derivative Test
First, a function must be differentiable (or at least continuous) near the point of interest. Next, it is necessary to locate critical points, which are points where f'(x) = 0 or f'(x) is undefined. To confirm whether each critical point is a local maximum, local minimum, or neither, the derivative’s sign is examined in intervals around that point.
However, remember that certain types of functions also require attention to endpoints if the interval is closed. Though endpoints are not always labeled “critical points,” they can be locations for local extrema too. Therefore, it is important not to ignore boundary points unless the problem specifically focuses on open intervals.
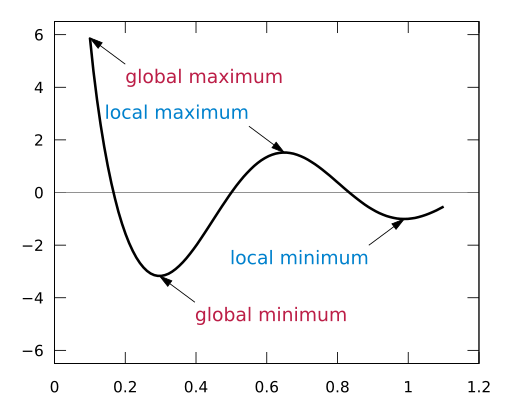
How to Find Local (Relative) Extrema
Identifying Critical Points
The first step in how to find relative extrema is discovering where the derivative equals zero or is undefined. Set f'(x) = 0 to find potential turning points. Also, verify that the derivative exists at those points. If the derivative does not exist, the point may still be critical, so do not skip that step.
For example, if f'(x) is undefined at x = a, that point might still be a location of local extrema. Always include such points in the analysis.
Applying the First Derivative Test
After identifying the critical points, determine the sign of f'(x) on intervals around each critical point. Some students use sign charts or tables to keep track of whether the function is increasing (f'(x) > 0) or decreasing (f'(x) < 0).
- If f'(x) changes from positive to negative at a critical point, that point is a local maximum.
- If f'(x) changes from negative to positive, that point is a local minimum.
- If f'(x) does not change sign, the point is not a local maximum or minimum.
Step-by-Step Example #1
Consider the function f(x) = x^3 - 3x^2 + 4. The goal is to use the first derivative test to find local extrema.
- Find the derivative: f'(x) = 3x^2 - 6x.
- Solve f'(x) = 0: 3x^2 - 6x = 0. Factor out 3x: 3x(x - 2) = 0. Hence, x = 0 or x = 2.
- Analyze intervals:
- For x < 0, pick a test value like x = -1. Then f'(-1) = 3(-1)^2 - 6(-1) = 3 + 6 = 9 > 0. So the function is increasing on that interval.
- Between 0 and 2, pick x = 1. Then f'(1) = 3(1)^2 - 6(1) = 3 - 6 = -3 < 0. The function is decreasing on (0, 2).
- For x > 2, pick x = 3. Then f'(3) = 3(3)^2 - 6(3) = 27 - 18 = 9 > 0. The function is increasing for x > 2.
- Classify critical points:
- At x = 0, the derivative changes from positive to negative, indicating a local maximum.
- At x = 2, the derivative switches from negative to positive, indicating a local minimum.
Therefore, x = 0 is a local maximum and x = 2 is a local minimum.
Step-by-Step Example #2
Now consider a rational function, g(x) = \frac{2x}{x - 1}. Apply the same method to find local (relative) extrema.
- Differentiate the function: g'(x) = \frac{(2)(x - 1) - (2x)(1)}{(x - 1)^2}. Simplify the numerator: g'(x) = \frac{2x - 2 - 2x}{(x - 1)^2} = \frac{-2}{(x - 1)^2}.
- Identify critical points: Since g'(x) = -2/(x - 1)^2, the fraction is never zero (the numerator is -2, which is constant). However, g'(x) is undefined at x = 1. Thus, x = 1 is a critical point because the derivative does not exist there.
- Analyze intervals around x = 1:
- For x < 1, pick x = 0. Then g'(0) = \frac{-2}{(0 - 1)^2} = \frac{-2}{1} = -2 < 0. This indicates that g(x) is decreasing on that interval.
- For x > 1, pick x = 2. Then g'(2) = \frac{-2}{(2 - 1)^2} = \frac{-2}{1} = -2 < 0. The function is also decreasing for x > 1.
- Classify the critical point: Since the derivative is negative on both sides of x = 1, there is no sign change. This means x = 1 is neither a local maximum nor a local minimum. Even though x = 1 is a critical point, the first derivative test reveals no local extrema there.
Common Pitfalls and Tips
- Failing to test both sides of a critical point leads to incomplete conclusions.
- Forgetting that some functions have points where the derivative is undefined can cause missing critical points.
- Listing intervals around each critical point helps visualize sign changes. It also reduces confusion by organizing values methodically.
- In some contexts, check endpoints for potential local extrema if the domain is closed, such as [a, b].
Quick Reference Chart
| Term | Definition |
| Critical Point | A point where f'(x) = 0 or f'(x) is undefined. |
| Local Maximum | A point where f'(x) changes from positive to negative. |
| Local Minimum | A point where f'(x) changes from negative to positive. |
| Relative Extrema | Another term for local maxima or minima. |
| First Derivative Test | A method that determines local maxima or minima by analyzing the sign of f'(x) around critical points. |
Conclusion
The first derivative test is a central idea in calculus for identifying local (relative) extrema. It explains when a function stops climbing and starts descending (local maximum) or when it transitions from falling to rising (local minimum). In 5.4 the first derivative test, students gain experience applying these steps, from taking the derivative to classifying the nature of critical points. Understanding what the first derivative test is prepares students for more advanced topics, such as the second derivative test and inflection points. Familiarity with how to find relative extrema across different types of functions will also build confidence in handling more complicated calculus problems.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 5.3 Determining Intervals on Which a Function Is Increasing or Decreasing
- 5.5 Using the Candidates Test to Determine Absolute (Global) Extrema
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








