Critical points play a major role in understanding a function’s behavior in calculus. They help determine where a function has a local maximum or minimum. Therefore, identifying these points and analyzing their behavior is essential for success in AP® Calculus AB and BC. The first and second derivative test both answer a key question: “What is the second derivative test, and how do these tests confirm the nature of critical points?” By considering sign changes and concavity, these methods provide a systematic way to determine local maxima and minima.
What We Review
Identifying Critical Points
Critical points are points on a function where its first derivative, f'(x), is zero or undefined. These points often signal potential maxima, minima, or inflection points. However, a function must be continuous at these points for the tests to apply cleanly.
It is also worth noting that, if there is only one critical point in a continuous function, it could be an absolute (global) maximum or minimum on that interval. This situation arises in certain special cases, as indicated by FUN-4.A.8 in AP® Calculus guidelines.
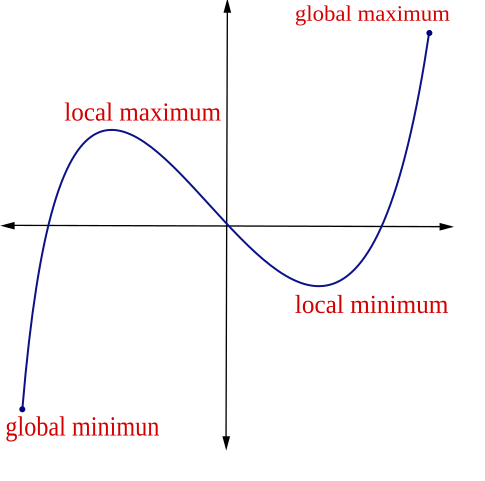
Example:
Consider the function f(x) = x^3 - 3x + 1.
- Find the first derivative: f'(x) = 3x^2 - 3.
- Solve for f'(x) = 0 to locate critical points: 3x^2 - 3 = 0 ⟹ x^2 = 1 ⟹ x = \pm 1.
- Confirm those points are defined in the original function: f(\pm 1) exist because the function is a polynomial, so both x = 1 and x = -1 are critical points.
Practice Problem:
Identify the critical points of g(x) = 2x^3 - 8x + 5.
- First, take the derivative g'(x) = 6x^2 - 8.
- Solve g'(x) = 0 to find potential critical points.
- Verify if each solution is defined in g(x) to conclude the critical points.
The First Derivative Test
Overview of the Method
The first derivative test is based on how the sign of f'(x) changes around a critical point. If the derivative changes sign from positive to negative, there is a local maximum. On the other hand, if it changes from negative to positive, there is a local minimum. However, if the sign does not change, the critical point might be neither a maximum nor a minimum.
Step-by-Step Example Using the First Derivative Test
Consider again f(x) = x^3 - 3x + 1, with critical points at x = -1 and x = 1.
- Write down the derivative: f'(x) = 3x^2 - 3.
- Determine sign intervals around the critical points:
- Interval 1: x < -1
- Interval 2: -1 < x < 1
- Interval 3: x > 1
- Pick test points in each interval, such as x = -2, x = 0, and x = 2.
- f'(-2) = 3(4) - 3 = 12 - 3 = 9 (positive)
- f'(0) = -3 (negative)
- f'(2) = 3(4) - 3 = 12 - 3 = 9 (positive)
- Analyze sign changes:
- From negative infinity to x = -1, f'(x) is positive.
- Between x = -1 and x = 1, f'(x) is negative.
- Beyond x = 1, f'(x) is positive.
- Conclusion about extrema:
- At x = -1, derivative changes from positive to negative, so there is a local maximum.
- At x = 1, derivative changes from negative to positive, so there is a local minimum.
The Second Derivative Test
What Is the Second Derivative Test?
The second derivative test uses f''(x), the derivative of f'(x), to determine the concavity of a function at a critical point. If f''(x) is positive at that point, the function is concave up, suggesting a local minimum. However, if f''(x) is negative, the function is concave down, indicating a local maximum. This approach is typically faster when the second derivative is easy to compute and is not zero at the critical point.
Step-by-Step Example Using the Second Derivative Test
Revisiting f(x) = x^3 - 3x + 1:
- Identify the critical points:
- From before, the critical points are x = -1 and x = 1.
- Find the second derivative: f'(x) = 3x^2 - 3, so f''(x) = 6x.
- Evaluate the second derivative at the critical points:
- f''(-1) = 6(-1) = -6 (negative, local maximum).
- f''(1) = 6(1) = 6 (positive, local minimum).
Practice Problem:
Use the second derivative test to classify the critical points of k(x) = x^4 - 8x^2 + 1.
- Find k'(x) and solve k'(x) = 0.
- Compute k''(x).
- Evaluate k''(x) at each critical point to confirm if it is a local maximum, minimum, or inconclusive.
Applying Both Tests in Practice
Sometimes, the first derivative test is more intuitive because it shows exactly how the sign of f'(x) changes. However, the second derivative test can be faster if the second derivative is straightforward to compute and is not zero at the critical point. Therefore, many problems in AP® Calculus are solved more efficiently with the second derivative test, unless it yields no clear sign (i.e., f''(x) = 0). In that case, returning to the first derivative test helps confirm whether there is a local extremum.
Example with Mixed Conditions (Optional Section)
If the second derivative test is inconclusive, try investigating the sign of f'(x) on either side of the point or use higher derivatives. However, for most standard problems, switching back to the first derivative test is enough to determine if a critical point is a local maximum, minimum, or neither.
Quick Reference Vocabulary Chart
| Term | Definition |
| Derivative | The slope of a function’s tangent line, found by differentiating (e.g., f'(x)). |
| Critical Point | A point x = c where f'(c) = 0 or f'(c) is undefined. |
| First Derivative Test | A method using the sign of f'(x) around a critical point to confirm maxima or minima. |
| Concavity | Indicates if a function curves upward or downward, based on f''(x). |
| Second Derivative Test | Uses f''(x) at a critical point to confirm maxima or minima (concavity). |
| Inflection Point | Where f''(x) changes sign, causing a change in concavity. |
| Local Extremum | A local maximum or minimum in a small region around a critical point. |
| Global Extremum | The absolute highest or lowest value of a function on an interval. |
Conclusion
The first and second derivative test together form reliable tools for analyzing critical points in AP® Calculus AB and BC. Therefore, it is key to practice finding critical points accurately, then deciding which test to use. Furthermore, ensuring that f''(x) is not zero before using the second derivative test can save time. Mastery of these approaches will make tackling more challenging optimization and analysis problems much more straightforward.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 5.6 Determining Concavity of Functions over Their Domains
- 5.8 Sketching Graphs of Functions and Their Derivatives
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








