The main goal here is to explain why this theorem is significant. It shows a deep link: integrals used to find area, displacement, or other quantities also define functions whose rates of change are given by the integrand. Therefore, the Fundamental Theorem of Calculus Part 1 becomes crucial for understanding many practical applications.

Statement of the Fundamental Theorem of Calculus Part 1

The Fundamental Theorem of Calculus Part 1 states that if f(t) is continuous on an interval containing a, then for the function

F(x) = \int_{a}^{x} f(t) dt

…the derivative \frac{d}{dx}\bigl[F(x)\bigr] equals f(x). This holds for all x in that interval.

Continuity matters because it ensures that f(t) behaves smoothly. If there are gaps or jumps, the simple relationship between the integral and the derivative might break. Furthermore, many standard applications require a continuous function to guarantee the integral is well-defined and nice enough to differentiate.

Defining New Functions Using Definite Integrals (FUN-5.A.1)

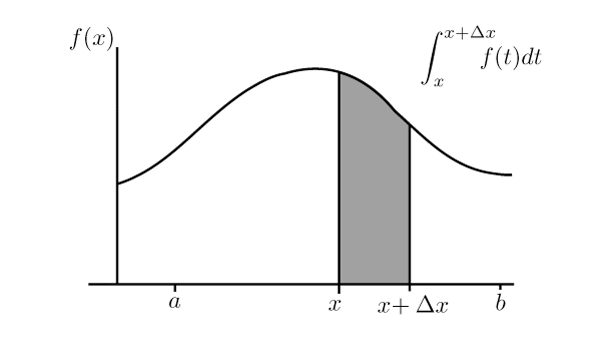
A definite integral not only calculates a single number—it can define an entire function. Specifically, setting

F(x) = \int_{a}^{x} f(t) dt

…means that as x changes, the upper bound of the integral changes. Consequently, F(x) captures the accumulated quantity from t=a to t=x.

Example #1

Let f(t) = t^2, and define

F(x) = \int_{0}^{x} t^2 dt.

Step-by-step solution:

1. First, compute the integral:

• \int_{0}^{x} t^2 dt can be found by the power rule for integrals.
• The antiderivative of t^2 is \frac{t^3}{3}.
• So, \int_{0}^{x} t^2 dt = \left[\frac{t^3}{3}\right]_0^x = \frac{x^3}{3} - 0 = \frac{x^3}{3}.

2. Therefore, F(x) = \frac{x^3}{3}.

3. Next, take the derivative of F(x) with respect to x:

• \frac{d}{dx} \left[\frac{x^3}{3}\right] = x^2.

4. Notice that this derivative x^2 matches f(x).

This example illustrates the fundamental idea: integrating f(t) then differentiating the result returns f(x), provided f is continuous.

Finding the Derivative of an Integral (FUN-5.A.2)

Figuring out how to find the derivative of an integral is simpler with the Fundamental Theorem of Calculus Part 1. When the upper limit is x, the derivative of an integral with bounds is just the integrand evaluated at the upper bound.

In symbols, for F(x) = \int_{c}^{x} f(t) dt, the derivative \frac{d}{dx}\bigl[F(x)\bigr] is f(x), again assuming continuity.

Sometimes, the upper limit might be another function, like g(x). In that case, the Chain Rule applies, and the derivative becomes f(g(x)) \cdot g'(x). However, that involves a slightly different scenario.

Example #2

Let f(t) = \cos(t), and define

G(x) = \int_{0}^{x} \cos(t) dt.

Step-by-step solution:

1. Find the antiderivative of \cos(t). The antiderivative is \sin(t).

2. Compute the definite integral:

• \int_{0}^{x} \cos(t) dt = \left[\sin(t)\right]_0^x = \sin(x) - \sin(0) = \sin(x).

3. So, G(x) = \sin(x).

4. Take the derivative:

• \frac{d}{dx}\bigl[\sin(x)\bigr] = \cos(x).

5. Observe that \cos(x) matches the original f(x).

This confirms that the derivative of an integral with bounds matches the integrand evaluated at the upper limit.

Special Situations and Practical Tips

Some special cases appear when there are more complex upper bounds. If the upper bound is a function g(x), then use the Chain Rule:

\frac{d}{dx} \left[\int_{a}^{g(x)} f(t) dt\right] = f\bigl(g(x)\bigr)\cdot g'(x).

Moreover, continuity plays a huge role in guaranteeing the smooth differentiation of integrals. If the function is not continuous, the process may require more advanced techniques or piecewise analysis.

Keep these reminders in mind:

• Always check if f(t) is continuous.
• Verify the variables in the bounds. If the bound is x, no extra chain rule is needed. If the bound is something else, be prepared to multiply by that derivative.

Quick Reference Chart (Vocabulary & Definitions)

Term/Concept	Definition/Explanation
Fundamental Theorem of Calculus Part 1	States that if f(t) is continuous on [a, x], the derivative of \int_{a}^{x} f(t)dt is f(x).
Definite Integral	The integral with specified limits that produces a real number, used to define new functions.
Continuous Function	A function with no breaks, jumps, or holes in its domain, essential for applying the theorem.
Derivative of an Integral with Bounds	The result of applying FTC Part 1, giving the original integrand evaluated at the upper bound.
Upper and Lower Bounds in an Integral	The limits of integration; for FTC Part 1, the upper bound typically contains the variable x.

Conclusion

The Fundamental Theorem of Calculus Part 1 unites two crucial concepts: the definite integral and the derivative. By defining a function as an integral of f(t), one sees that differentiating it returns f(x). This discovery underpins many calculus methods in AP® Calculus AB-BC and beyond. Therefore, understanding how to find the derivative of an integral helps solve problems involving area, rates, and other real-world applications. Ultimately, this theorem’s clear statement about the derivative of an integral with bounds reinforces the idea that differentiation and integration are deeply connected.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.