U-substitution is a powerful technique used to simplify integrals, which often appear in AP® Calculus AB-BC questions. It is especially useful when facing complicated expressions. Therefore, understanding how to identify and apply a strategic substitution can help solve integrals more easily. Both definite and indefinite integrals can become more manageable with this approach, especially when working through u substitution practice problems.
This article explores the essentials of u-substitution. It includes why it simplifies integrals, how to apply the method step by step, and how to adapt the process for definite integrals. The goal is to help you master key integration u-substitution practice problems, ensuring you are ready for 6.9 integrating using substitution and beyond.
What We Review
Understantding U-Substitution
What Is U-Substitution?
U-substitution is a method where a new variable, u, represents an appropriate portion of the integrand. By doing this, a difficult integral in terms of x transforms into a simpler integral in terms of u. This technique is closely connected to the 6.9 integrating using substitution curriculum reference.
U-substitution practice problems reveal how beneficial it is for tackling nested functions and complicated expressions. It lets you rewrite the problem in a more familiar form, often resembling integrals you already know.
Basic Setup of U-Substitution
- Identify the part of the integrand that seems complex (often an inner function).
- Let u be that inner function.
- Then find du, which is the derivative of u times dx.
- Replace all expressions involving x with expressions in terms of u.
Common functions for u are exponents, trigonometric inner functions, or denominators that simplify upon being substituted.
Indefinite Integrals Using U-Substitution
Step-by-Step Procedure
- Identify the most complicated part of the integrand as your “inner function.”
- Let u = \text{(inner function)}.
- Compute du = \frac{du}{dx} dx.
- Rewrite the original integral, substituting u and du.
- Integrate with respect to u.
- Substitute back to x to get the final answer.
Example 1: A Basic Indefinite Integral
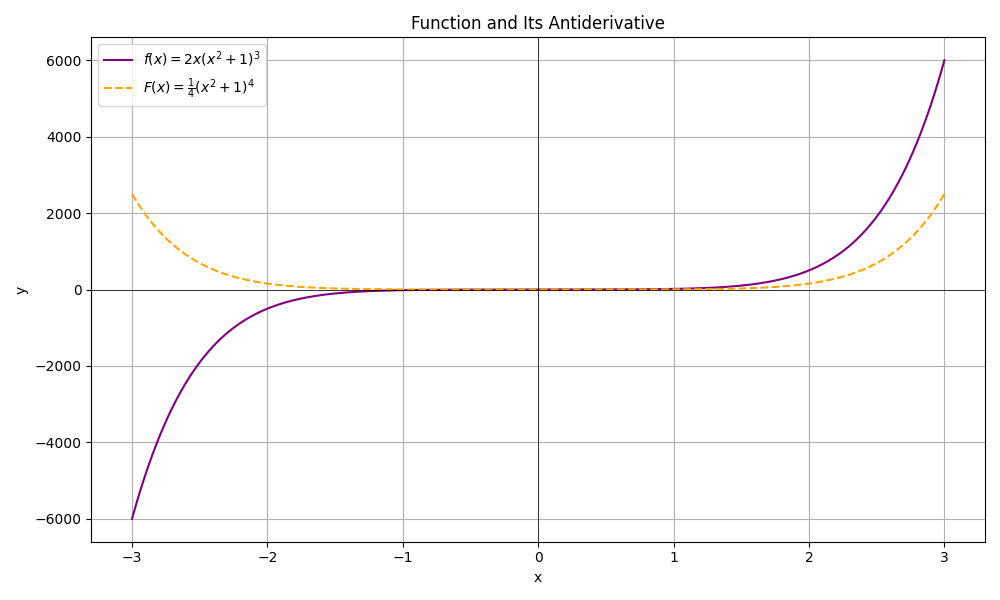
Consider the integral: \int 2x (x^2 + 1)^3 dx
Step-by-Step Solution:
- Identify the inner function as x^2 + 1.
- Let u = x^2 + 1.
- Differentiate: du = 2x dx. Notice this matches the 2x dx in the integral.
- Rewrite the integral in terms of u: \int 2x (x^2 + 1)^3 dx = \int u^3 du.
- Integrate: \int u^3 du = \frac{u^4}{4} + C.
- Substitute back u = x^2 + 1: \frac{(x^2 + 1)^4}{4} + C.
Therefore, the final answer is: \frac{(x^2 + 1)^4}{4} + C.
Example 2: Another Indefinite Integral
Let’s solve a trigonometric example: \int \sin(3x) dx
Step-by-Step Solution:
- Choose the inner function 3x, since that will simplify the integral.
- Let u = 3x.
- Then du = 3 dx, or dx = \frac{du}{3}.
- Rewrite the integral: \int \sin(3x) dx = \int \sin(u) \cdot \frac{du}{3}.
- Factor out the constant: \frac{1}{3} \int \sin(u) du.
- Integrate \sin(u): \frac{1}{3}(-\cos(u)) + C.
- Substitute back u = 3x: -\frac{1}{3}\cos(3x) + C.
Hence, the solution is: -\frac{1}{3}\cos(3x) + C.
These u-substitution practice problems show how focusing on the inner function simplifies everything.
Definite Integrals Using U-Substitution
Adjusting the Limits of Integration
When solving definite integrals, remember to change the limits of integration from x values to u values. After substituting u, do not revert back to x until the end, unless you prefer to switch back and then plug the original x-bounds.
Example 3: A Definite Integral
Evaluate the definite integral: \int_{0}^{2} x (2x + 1)^2 dx
Step-by-Step Solution:
- Choose your inner function. Here, u = 2x + 1.
- Differentiate: du = 2 dx, so dx = \frac{du}{2}.
- Convert the x-limits into u-limits: When x = 0, u = 2(0) + 1 = 1. When x = 2, u = 2(2) + 1 = 5.
- Notice we still have x in the integrand. Express x in terms of u. From u = 2x + 1, we get x = \frac{u - 1}{2}.
- Rewrite the integral: \int_{x=0}^{x=2} x (2x + 1)^2 dx = \int_{u=1}^{u=5} \left(\frac{u - 1}{2}\right) u^2 \cdot \frac{du}{2}.
- Simplify inside the integral: \int_{1}^{5} \frac{(u - 1) u^2}{4} du. This becomes \int_{1}^{5} \frac{u^3 - u^2}{4} du.
- Factor out the constant \frac{1}{4}: \frac{1}{4}\int_{1}^{5} (u^3 - u^2) du.
- Integrate term by term: \frac{1}{4} \left[ \frac{u^4}{4} - \frac{u^3}{3} \right]_{u=1}^{u=5}.
- Evaluate at u=5 and u=1: \frac{1}{4} \left[ \left(\frac{5^4}{4} - \frac{5^3}{3}\right) - \left(\frac{1^4}{4} - \frac{1^3}{3}\right)\right].
- Compute the result:
- For u=5: \frac{5^4}{4} = \frac{625}{4}, and \frac{5^3}{3} = \frac{125}{3}.
- For u=1: \frac{1}{4} - \frac{1}{3} = \frac{3}{12} - \frac{4}{12} = -\frac{1}{12}.
Putting it all together yields a numerical value. It is completely fine to leave the result as a fraction: \frac{1}{4} \left[ \left(\frac{625}{4} - \frac{125}{3}\right) + \frac{1}{12} \right].
That simplifies further, but even in fractional form, it is correct.
Common Mistakes to Avoid
- Forgetting to convert the limits of integration when switching to u.
- Mixing up du with the derivative of u.
- Failing to express remaining x-terms in terms of u.
Common Pitfalls and Strategies for Success
- Overlooking simple algebraic manipulations before applying u-substitution can cause extra complexity.
- Misidentifying the best choice for u is easy if you do not look for the function inside another function.
- Strategies to quickly identify u include looking for a chain rule pattern. If the integrand has a product of a function and the derivative of that function (or something close to it), that function is usually your u.
- Always check your work by differentiating the final answer. If it matches the original integrand, the process is correct.
Quick Reference Chart: Vocabulary and Definitions
| Term | Definition |
| U-Substitution | A technique to simplify integrals by choosing a new variable u for the “inner function.” |
| Inner Function | The function that appears nested inside another function or as part of a composite function. |
| du | The differential of u, representing \frac{du}{dx} dx. |
| Indefinite Integral | The set of antiderivatives of a function, including a constant of integration. |
| Definite Integral | The integral of a function with specific upper and lower limits, producing a numerical value. |
Conclusion
U-substitution is one of the most important integration techniques on the AP® Calculus AB-BC exam. With enough practice on a variety of u-substitution practice problems, students can gain confidence in recognizing when this method is applicable. Therefore, it is essential to practice these steps often.
Mastering this skill for both definite and indefinite integrals ensures preparedness for 6.9 integrating using substitution and other exam topics. In fact, repeated exposure to integration u-substitution practice problems is the best way to build confidence. Keep exploring additional examples and variations, and soon the chain rule within integration will feel like second nature.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








