Integration using completing the square is a valuable technique for tackling hard integrals. In advanced calculus courses, students often face integrals that cannot be solved with simple formulas. Therefore, understanding how to rewrite quadratic expressions into a perfect square form is critical. This article offers a clear explanation of how completing the square can simplify integrals. It also highlights how extra steps like polynomial long division may help with more complex cases. By the end, students will know how to spot opportunities for using these methods and how to apply them effectively.
What We Review
Why “Completing the Square” Matters for Integration
Completing the square in algebra involves rewriting a quadratic expression in a way that reveals a neat square structure. For example, x^2 + 4x + 5 can be turned into (x + 2)^2 + 1. When working with integrals, this approach can transform difficult forms into something more familiar, such as those leading to an arctangent or a logarithm.
This method is especially helpful for hard integrals that have quadratic denominators. In many integrals that appear in AP® Calculus AB and BC, partial fractions or direct substitution might not work until the expression is rewritten. Therefore, completing the square becomes the key that unlocks the solution.
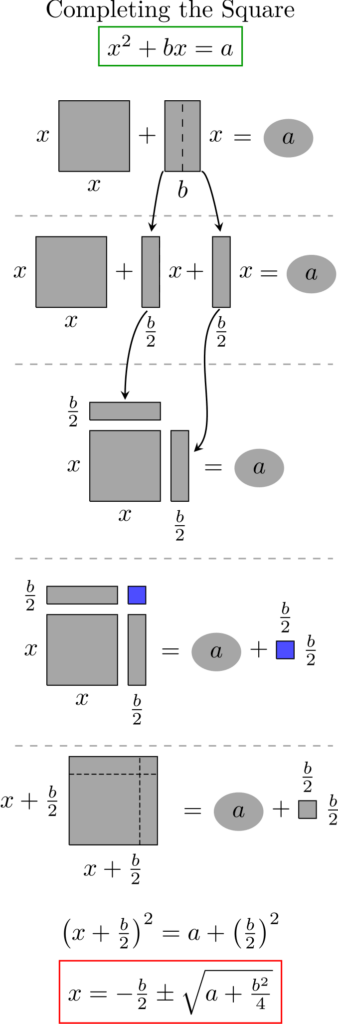
Step-by-Step Method: Integration Using Completing the Square
Overview of the Process
- Identify a quadratic expression inside the integral.
- Complete the square by rewriting the quadratic in the form (x - h)^2 + k.
- Recognize common integral patterns (like \int \frac{dx}{(x-a)^2 + b^2}), which lead to known antiderivatives such as arctangent.
- Integrate carefully, keeping track of any constants or negative signs.
Example 1: Basic Completing the Square
Consider the integral \int \frac{dx}{x^2 + 4x + 5}.
Step-by-Step Solution
- Notice that the denominator is a quadratic: x^2 + 4x + 5.
- Complete the square:
- Rewrite as x^2 + 4x + 5 = (x^2 + 4x + 4) + 1.
- This becomes (x + 2)^2 + 1.
- Rewrite the integral: \int \frac{dx}{(x + 2)^2 + 1}.
- Use the standard form \int \frac{d(u)}{u^2 + 1} = \arctan(u) + C. Here, let u = x + 2. Then du = dx.
- Integrate: \int \frac{du}{u^2 + 1} = \arctan(u) + C.
- Substitute back u = x + 2: \arctan(x + 2) + C.
Therefore, the final answer is \arctan(x + 2) + C. Every piece of the process—especially completing the square—makes the integral straightforward.
Example 2: Variations and Special Cases
Consider a more complex integral: \int \frac{dx}{2x^2 + 8x + 10}.
Step-by-Step Solution
- Factor out the coefficient of x^2 from the denominator to manage the expression: 2x^2 + 8x + 10 = 2(x^2 + 4x + 5).
- Rewrite the integral: \int \frac{dx}{2(x^2 + 4x + 5)} = \frac{1}{2} \int \frac{dx}{x^2 + 4x + 5}.
- From Example 1, complete the square in the denominator: x^2 + 4x + 5 = (x + 2)^2 + 1.
- So the integral becomes: \frac{1}{2} \int \frac{dx}{(x + 2)^2 + 1}.
- Set u = x + 2. Then du = dx. The integral now is: \frac{1}{2} \int \frac{du}{u^2 + 1}.
- Apply the known antiderivative: \frac{1}{2} \arctan(u) + C.
- Substitute back u = x + 2: \frac{1}{2} \arctan(x + 2) + C.
This example shows how a simple factor change adjusts the final result. However, the process remains the same: complete the square, substitute, and integrate.
Additional Techniques for Hard Integrals
Rearranging into Equivalent Forms
Sometimes, integrals with higher-degree polynomials can still use integration using completing the square. However, the expression might first need polynomial long division. This splits the integrand into simpler components. If the result still contains a quadratic, completing the square may return an integral that matches a standard form.
Partial fraction decomposition is another method. It shines in rational expressions where the denominator factors into linear or irreducible quadratic terms. In many cases, though, completing the square for any irreducible quadratic factor is the best next step.
Example: Combining Completing the Square with Other Methods
Consider a more advanced integral: \int \frac{x^3 + 2x^2 + x + 1}{x^2 + 4x + 5} dx.
Step-by-Step Solution
- First, apply polynomial long division to simplify the fraction. Divide x^3 + 2x^2 + x + 1 by x^2 + 4x + 5.
- The division may produce a polynomial plus a remainder term. Suppose the result is Q(x) + \frac{R(x)}{x^2 + 4x + 5}, where Q(x) is the quotient and R(x) is the remainder.
- Integrate Q(x) easily using power rules.
- For the term with the remainder, notice x^2 + 4x + 5. Complete the square: (x + 2)^2 + 1.
- Integrate this part using the same approach shown in Example 1.
- Combine all results to get the final antiderivative.
As a result, rewriting the integral first with polynomial long division, then completing the square, solves an otherwise complicated problem.
Key Takeaways and Best Practices
- Comfort with algebraic manipulations is essential for success with hard integrals.
- Completing the square greatly simplifies quadratic denominators, transforming them into recognizable forms.
- When polynomials are more complex, consider polynomial long division first, then completing the square if needed.
- Know that partial fraction decomposition can also help if the denominator factors nicely.
- Watch for constant factors and negative signs to avoid mistakes.
Quick Reference Chart: Important Vocabulary and Definitions
| Term/Concept | Definition/Explanation |
| Completing the Square | A technique for rewriting a quadratic expression in the form (x – h)² + k. |
| Polynomial Long Division | A method for dividing polynomials, helpful for turning a complex rational integrand into a simpler expression, sometimes necessary before completing the square. |
| Equivalent Forms | Different algebraic representations of the same expression, often used to make an integral more recognizable for standard integration techniques. |
Conclusion
Integration using completing the square is a powerful way to handle challenging calculus problems. Hard integrals often become more manageable once the quadratic expressions are expressed in perfect square form. Furthermore, combining this technique with polynomial long division or partial fraction decomposition broadens the range of integrals that can be tackled.
Consistent practice with these methods helps build confidence and speed. In AP® Calculus AB-BC, mastering these tools can significantly boost problem-solving skills. By recognizing when to complete the square, students become more efficient at spotting patterns and finding neat antiderivatives.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








