Integral calculus techniques play a central role in AP® Calculus AB-BC. These powerful methods help solve challenging problems involving areas, volumes, and other applications in mathematics and science. Therefore, understanding the core principles behind these integration techniques makes problem-solving more efficient and reliable. Moreover, practicing various integral practice problems builds confidence for future exams and advanced math courses.

This guide explores the most important integration techniques, including:

• Basic power rule integration
• Substitution (u-substitution)
• Integration by parts
• Partial fractions
• Special trigonometric integrals

Throughout, there will be step-by-step solutions to examples. Each section ends with a clearer sense of why that technique is useful.

Fundamental Concepts in Integral Calculus

Definitions and Key Ideas

An integral can be indefinite or definite. An indefinite integral is written as \int f(x)dx and represents the family of all antiderivatives of f(x). The general form includes a constant of integration, C, because there are infinitely many antiderivatives. On the other hand, a definite integral \int_{a}^{b} f(x)dx is associated with an area under the curve, from x=a to x=b.

The process of finding antiderivatives relies on rules such as the power rule. Therefore, understanding the power rule is the first step to mastering more advanced integral calculus techniques.

Example: Basic Power Rule Integration

Consider the function f(x) = 4x^3. Find the indefinite integral.

1. Rewrite the problem: \int 4x^3dx
2. Apply the power rule for integration:
   • Recall that \int x^ndx = \frac{x^{n+1}}{n+1} + C for n \neq -1.
   • For 4x^3, factor out the constant 4: 4 \int x^3dx.
3. Integrate x^3 using the power rule: \int x^3dx = \frac{x^{4}}{4} + C.
4. Combine and simplify: 4 \cdot \frac{x^{4}}{4} + C = x^4 + C.

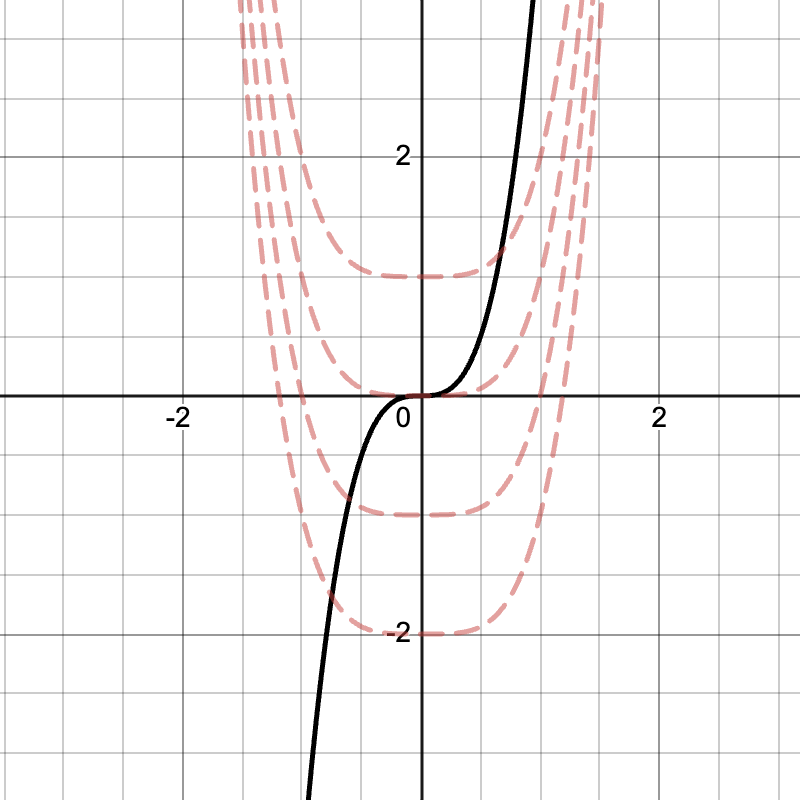
So, the antiderivative of 4x^3 is x^4 + C. Here is a visual of the original function graphed with a few of its possible antiderivatives with different C values.

Essential Integration Techniques

Substitution Method (u-substitution)

Explanation in Simple Terms

Substitution helps simplify integrals by introducing a new variable u. It is particularly useful if an integrand contains a function and its derivative. For instance, whenever a part of a function looks like a derivative of another inner function, consider letting u represent that inner function. Consequently, this reduces the integral to a simpler form.

Example and Step-by-Step Solution

Evaluate \int x \cos(x^2)dx.

1. Notice that x^2 is inside the cosine function. Its derivative is 2x.
2. Let u = x^2. Then du = 2xdx.
3. Rewrite xdx in terms of du: xdx = \frac{du}{2}.
4. Substitute everything back: \int x \cos(x^2)dx = \int \cos(u) \cdot \frac{du}{2}.
5. Factor out the constant \frac{1}{2}: \frac{1}{2} \int \cos(u)du.
6. Integrate \cos(u): \int \cos(u)du = \sin(u) + C.
7. Hence, the result is: \frac{1}{2}\sin(u) + C = \frac{1}{2}\sin(x^2) + C.

Integration by Parts

Explanation in Simple Terms

Integration by parts is based on the product rule of differentiation. The formula is: \int udv = uv - \int vdu. This approach is especially helpful when the integrand looks like a product of two different types of functions (e.g., polynomials with exponentials, polynomials with ln, or polynomials with trig). To decide which part is u and which part is dv, many students follow the LIATE rule (Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, Exponential).

Example and Step-by-Step Solution

Compute \int x e^xdx.

1. Choose u and dv:
   • Let u = x, which makes du = dx.
   • Let dv = e^xdx, because \int e^xdx = e^x. Hence, v = e^x.
2. Apply the formula: \int x e^xdx = x e^x - \int e^x \cdot 1dx.
3. Simplify: x e^x - \int e^xdx.
4. Integrate \int e^xdx: e^x + C.
5. So the complete answer is: x e^x - e^x + C = e^x(x - 1) + C.

Partial Fractions

Explanation in Simple Terms

Partial fraction decomposition is used to rewrite a complicated rational expression as a sum of simpler terms. This technique is crucial when the integrand is a fraction whose numerator and denominator are polynomials. Therefore, partial fractions break down a ratio into forms that are easier to integrate directly.

Example and Step-by-Step Solution

Find \int \frac{2x+1}{x^2 + x}dx.

1. Factor the denominator: x^2 + x = x(x+1).
2. Decompose: \frac{2x+1}{x(x+1)} = \frac{A}{x} + \frac{B}{x+1}.
3. Combine into a single fraction: \frac{A(x+1) + Bx}{x(x+1)}.
4. Match coefficients:
   • Numerator: A(x+1) + Bx = Ax + A + Bx = (A+B)x + A.
   • Compare to 2x + 1. Thus, A + B = 2 and A = 1.
5. Solve for A and B:
   • A = 1.
   • 1 + B = 2 \Rightarrow B = 1.
6. Rewrite the integral: \int \frac{2x+1}{x(x+1)}dx = \int \left(\frac{1}{x} + \frac{1}{x+1}\right) dx.
7. Integrate each term: \int \frac{1}{x}dx = \ln|x| and \int \frac{1}{x+1}dx = \ln|x+1|.
8. Final answer: \ln|x| + \ln|x+1| + C = \ln|x(x+1)| + C.

Special Trigonometric Integrals

Explanation in Simple Terms

Certain trigonometric integrals occur so often that it helps to memorize them. For example, \int \sin(x)dx, \int \cos(x)dx, and \int \sec^2(x)dx appear in many problems. Moreover, knowing fundamental identities such as \sin^2(x) + \cos^2(x) = 1 can simplify complicated expressions.

Example and Step-by-Step Solution

Compute \int \sin(x)\cos(x)dx.

1. Recognize that either u = \sin(x) or u = \cos(x) can work.
2. Let u = \sin(x). Then du = \cos(x)dx.
3. The integral becomes: \int u du.
4. Integrate: \int udu = \frac{u^2}{2} + C = \frac{\sin^2(x)}{2} + C.

Strategies for Identifying the Right Integration Technique

Classification of the Integrand

Polynomial expressions often suggest direct power rule or partial fractions. Meanwhile, exponential and trigonometric functions sometimes call for substitution or integration by parts. Therefore, it helps to look for inner functions paired with derivatives to guide the choice of u-substitution. If there is a product of distinct functions, integration by parts might be best.

Decision Process

Here is a brief approach:

• Step 1: Check for a straightforward power rule or trig rule.
• Step 2: Look for a function-derivative pattern (u-substitution).
• Step 3: Try integration by parts if the integrand involves a product of different function types.
• Step 4: Use partial fractions if the integrand is a rational function and can be factored.

Example: Mixed Function

Determine \int x \ln(x)dx.

1. Observe the product: x (algebraic) and \ln(x) (logarithmic).
2. Integration by parts is a good candidate.
3. Let u = \ln(x), so du = \frac{1}{x}dx. Then dv = xdx, which means v = \frac{x^2}{2}.
4. Apply the formula: \int x \ln(x)dx = \frac{x^2}{2}\ln(x) - \int \frac{x^2}{2} \cdot \frac{1}{x}dx.
5. Simplify the second term: \int \frac{x^2}{2} \cdot \frac{1}{x}dx = \int \frac{x}{2}dx = \frac{1}{2}\int xdx = \frac{x^2}{4} + C.
6. Put it all together: \frac{x^2}{2}\ln(x) - \frac{x^2}{4} + C.

Quick Reference Chart: Key Terms and Definitions

Term	Definition
Integrand	The function being integrated.
Bounds	The limits of integration a and b in a definite integral.
Indefinite Integral	The antiderivative plus a constant of integration, C.
Definite Integral	The integral evaluated between two bounds, representing a net area or accumulation.
u-substitution	Method where u is chosen to simplify the integrand.
Integration by Parts	Technique based on \int u dv = uv - \int v du.

Conclusion

In summary, integral calculus techniques range from simple power rule applications to more involved methods like u-substitution, integration by parts, partial fractions, and special trigonometric integrals. Consistent practice with integral practice problems helps build familiarity, which is vital for AP® Calculus AB-BC success. Therefore, it is helpful to develop a systematic approach to identifying which integration technique applies to each integrand. Mastery of these methods allows for confident progress into more advanced topics and real-world applications in mathematics, physics, and engineering.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.