Understanding how to handle the derivative of parametric equations is essential for success in AP® Calculus AB-BC. These equations appear in many contexts, including motion problems and modeling real situations. Moreover, a solid grasp of differentiation in a parametric context reveals the slope of tangent lines and rates of change. This guide explains the core ideas and then walks through examples step by step.

Parametric equations express both x and y in terms of a third variable, often t. When viewed together, the pair (x(t), y(t)) traces a path in the coordinate plane. Learning to find \frac{dy}{dx} helps in understanding how quickly y changes compared to x. This derivative is necessary for determining tangent line slopes and related motion problems.

Recognizing the significance of parametric equations also supports mastery of AP® Calculus standards, such as CHA-3.G.1 and CHA-3.G.2. These learning objectives include interpreting and analyzing functions in parametric form for the AB level, as well as dealing with advanced scenarios in BC.

Understanding Parametric Equations

Basic Definition

A parametric equation describes x and y each as separate functions of a third variable:

x(t) and y(t).

For instance, x(t) = 2t + 1 and y(t) = 3t - 4 define a line when t varies. Many paths and curves can be generated by choosing different functional forms for x(t) and y(t). Parametric equations frequently appear in real-world modeling, such as in projectile motion or describing an object traveling along a curve.

Relevance in AP® Calculus

These functions are tightly connected to the College Board’s curriculum. Understanding them is critical for solving problems in:

• Tangent line slope calculations
• Rate-of-change questions in multiple variables
• Graphing curves not easily expressed as y in terms of x

Both the AB and BC courses address parametric curves. Therefore, thorough preparation ensures confidence during the exam.

The Concept of the Derivative for Parametric Equations

Derivative as Slope of Tangent

In calculus, the slope of the tangent line to a curve at a point is given by \frac{dy}{dx}. For parametric equations, \frac{dy}{dx} still measures how y changes with respect to x, but both x and y depend on t. Therefore, the slope of the tangent line at any parameter value t depends on the derivatives \frac{dx}{dt} and \frac{dy}{dt}.

Primary Formula

The key formula states:

\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}

…provided that \frac{dx}{dt} \neq 0. If \frac{dx}{dt} = 0 at some parameter value, then the tangent line may be vertical or undefined, so that scenario requires careful analysis.

Step-by-Step Approach to Differentiation (Parametric Equations)

1. Differentiate x(t) with respect to t. This yields \frac{dx}{dt}.
2. Differentiate y(t) with respect to t. This yields \frac{dy}{dt}.
3. Compute \frac{dy}{dx} by dividing \frac{dy}{dt} by \frac{dx}{dt}.
4. If \frac{dx}{dt} equals 0 at a certain t-value, interpret that point carefully (possibly a vertical tangent).

By following these steps, it is possible to find the slope of the tangent line for any valid parametric equation.

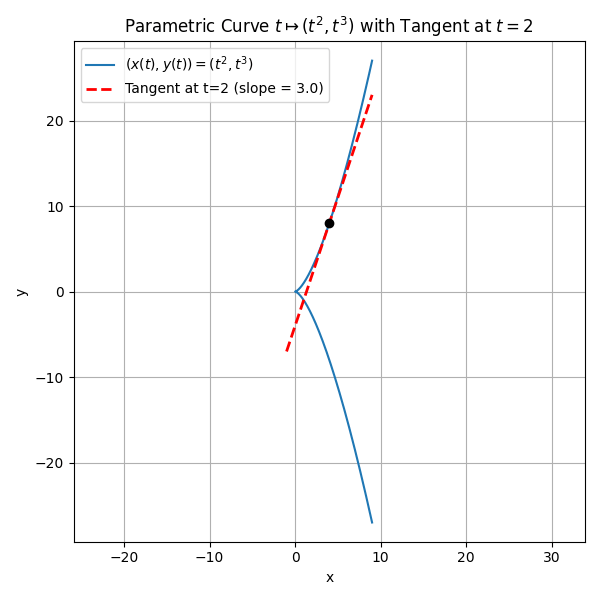
Example 1: Introductory Problem

Consider one of the simpler parametric equations:

x(t) = t^2, \quad y(t) = t^3.

Find \frac{dy}{dx} at t = 2.

Step-by-Step Solution

1. Differentiate x(t) = t^2 with respect to t to get\frac{dx}{dt} = 2t.
2. Differentiate y(t) = t^3 with respect to t to get\frac{dy}{dt} = 3t^2.
3. Compute \frac{dy}{dx} as\frac{dy}{dx} = \frac{3t^2}{2t}.
   • Simplify if t \neq 0, so it becomes\frac{dy}{dx} = \frac{3t^2}{2t} = \frac{3t}{2}.
4. Evaluate at t = 2:
   • \frac{dy}{dx}\bigg\rvert_{t=2} = \frac{3(2)}{2} = 3.

Hence, the slope of the tangent line at t=2 is 3.

Example 2: Intermediate Problem with Trigonometric Functions

Now consider the following parametric equations:

x(t) = 2\sin(t), \quad y(t) = 3\cos(t).

Find \frac{dy}{dx} at t = \frac{\pi}{2}.

Step-by-Step Solution

1. Differentiate x(t) = 2\sin(t) with respect to t to get\frac{dx}{dt} = 2\cos(t).
2. Differentiate y(t) = 3\cos(t) with respect to t to get\frac{dy}{dt} = -3\sin(t).
3. Compute \frac{dy}{dx} as\frac{dy}{dx} = \frac{-3\sin(t)}{2\cos(t)}.
4. Evaluate at t = \frac{\pi}{2}: Since \cos(\frac{\pi}{2}) = 0, the denominator 2\cos(t) is zero. This indicates a potential vertical tangent. Formally, \frac{dy}{dx} is undefined at that parameter value, suggesting a vertical slope.

Derivative of Parametric Equations: Practice Problem

Try this quick exercise:

Given x(t) = 4t - 1 and y(t) = t^2 + 2, find \frac{dy}{dx} at t = 3.

Step-by-Step Solution

1. Differentiate x(t) = 4t - 1: \frac{dx}{dt} = 4.
2. Differentiate y(t) = t^2 + 2: \frac{dy}{dt} = 2t.
3. Compute \frac{dy}{dx}: \frac{dy}{dx} = \frac{2t}{4} = \frac{t}{2}.
4. Evaluate at t = 3: \frac{dy}{dx}\bigg\rvert_{t=3} = \frac{3}{2}.

Therefore, the slope at t=3 is \frac{3}{2}.

Quick Reference Chart (Terminology and Definitions)

Term	Definition
Parametric Equation	A set of two functions x(t),;y(t) defining x and y in terms of a third variable t.
\frac{dx}{dt}, \frac{dy}{dt}	Derivatives of x(t) and y(t) with respect to t.
\frac{dy}{dx}	The slope of the tangent line, found by dividing \frac{dy}{dt} by \frac{dx}{dt}.
Tangent Line Slope	The instantaneous slope at a point defined by a parametric function.

Conclusion

Finding the derivative of parametric equations is a crucial skill for AP® Calculus AB-BC. The process requires differentiating both x(t) and y(t) with respect to t, then using the quotient \frac{dy}{dt} \div \frac{dx}{dt}. It is equally important to watch for points where \frac{dx}{dt} is zero, because the slope may be infinite or undefined.

Overall, the derivative of parametric equations reveals a deeper understanding of how these curves behave and how fast they change in different directions. Practice and familiarity with these steps build confidence, especially when working on tangent lines or rate-of-change problems in real-world contexts. Mastery of this topic will streamline success in both the AB and BC curricula, reinforcing the power of calculus in modeling and problem-solving.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.