Introduction

Particle motion is a major topic in AP® Calculus AB-BC. It explores how velocity, speed, and acceleration help describe a particle’s movement along a line or curve. Understanding these ideas can answer two key questions: “When is a particle at rest?” and “When does a particle change direction?” Therefore, learning to work with derivatives and integrals of the position function becomes essential. These concepts also connect with standards FUN-8.B.1 and FUN-8.B.2. Moreover, they introduce the building blocks for topics like instantaneous velocity calculus and speed formula calculus.

Below, the most important ideas in particle motion are broken down step by step. Pay attention to how the derivative and integral each play a role. By the end, it will be clearer how to handle questions about a particle’s rest and direction changes.

Key Concepts in Particle Motion

Velocity vs. Speed

Velocity measures how quickly position changes. In calculus, velocity is the derivative of the position function. If s(t) is the position function, then its derivative is:

v(t) = s'(t)

Velocity can be positive or negative, indicating direction along a straight line. Speed, on the other hand, is always the magnitude of velocity. Therefore, speed is never negative. For a velocity v(t), its speed is \lvert v(t) \rvert.

Acceleration

Acceleration describes how velocity changes over time. In calculus terms, acceleration is the derivative of velocity:

a(t) = v'(t)

An object speeds up when velocity and acceleration have the same sign, and it slows down when they have opposite signs. Therefore, checking acceleration can sometimes reveal whether a particle’s direction is about to change.

Position and Displacement

The position function s(t) shows a particle’s location along an axis at time t. The particle’s displacement from time t = a to t = b is the net change in position:

\text{Displacement} = s(b) - s(a)

However, total distance traveled accounts for every bit of movement, even if the particle changes direction. This distinction matters because speed formula calculus often requires tracking the absolute value of velocity.

Conditions: When Is a Particle at Rest?

A particle is at rest when its velocity equals zero. This means solving v(t) = 0 will reveal any times when the particle’s motion stops. However, it is also important to look at velocity’s sign before and after these times. Doing so indicates whether the particle simply stops momentarily or changes its direction completely.

Example (Step-by-Step): Finding a Time When a Particle Is at Rest

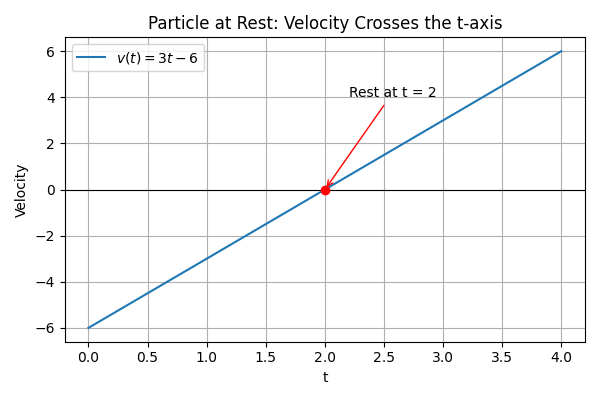
1. Suppose the velocity function is v(t) = 3t - 6.
2. To find when the particle is at rest, set v(t) = 0:
   • 3t - 6 = 0\rigtharrow t = 2\rightarrow3t = 6
3. Therefore, the particle is at rest at t = 2.

Practice Problem:

Let v(t) = t^2 - 4t + 3. Determine the time(s) when the particle is at rest.

Step 1: Set t^2 - 4t + 3 = 0.

Step 2: Factor if possible: (t - 3)(t - 1) = 0.

Step 3: The solutions are t = 1 and t = 3. These are the times when the particle is at rest.

When Does a Particle Change Direction?

A particle changes direction when its velocity changes sign (for instance, from positive to negative or vice versa). Therefore, one must check intervals around the times when v(t) = 0. Additionally, acceleration can help confirm whether the velocity shifts from increasing to decreasing or the opposite.

Example (Step-by-Step): Identifying When a Particle Stops (vector-valued function)

Consider the vector-valued function
\vec{r}(t) = \langle t^2, \sin(t) \rangle,
which represents the position of a particle in the plane as a function of time.

To determine when the particle stops, we need to find when its velocity vector is zero.

Step 1: Find the Velocity Function

Differentiate the position vector with respect to t:

\vec{v}(t) = \dfrac{d}{dt} \langle t^2, \sin(t) \rangle = \langle 2t, \cos(t) \rangle

Step 2: Set the Velocity Vector Equal to Zero

A particle stops when both components of the velocity vector are zero:

2t = 0 → t = 0
\cos(t) = 0 → t = \dfrac{\pi}{2}, \dfrac{3\pi}{2}, \dots

So we need to find when both equations are satisfied at the same time.

Step 3: Check for Simultaneous Solutions

• t = 0 → 2t = 0 ✅, \cos(0) = 1 ❌
• t = \dfrac{\pi}{2} → 2t \ne 0 ❌
• None of the values of t that make \cos(t) = 0 also make 2t = 0

✅ Final Answer:

The particle never completely stops because there is no time when both components of the velocity vector are simultaneously zero.

Example (Step-by-Step): Identifying Direction of Motion (vector-valued function)

Consider the vector-valued position function
\vec{r}(t) = \langle \cos(t) , \sin(t) \rangle.

This function represents a particle moving around the unit circle in the plane as time increases.

Step 1: Find the Velocity Function

Differentiate each component of the position function:

\vec{v}(t) = \dfrac{d}{dt} \langle \cos(t), \sin(t) \rangle = \langle -\sin(t), \cos(t) \rangle

This velocity vector tells us the direction in which the particle is moving at each moment.

Step 2: Analyze the Velocity Vector at Specific Times

Let’s evaluate the velocity vector at key points around the circle:

First, at t = 0:
\vec{v}(0) = \langle -\sin(0), \cos(0) \rangle = \langle 0, 1 \rangle
→ Now, the particle is moving straight up.

At t = \dfrac{\pi}{2}:
\vec{v}\left(\dfrac{\pi}{2}\right) = \langle -1, 0 \rangle
→ Here, the particle is moving left.

For t = \pi:
\vec{v}(\pi) = \langle 0, -1 \rangle
→ Next, the particle is moving down.

At t = \dfrac{3\pi}{2}:
\vec{v}\left(\dfrac{3\pi}{2}\right) = \langle 1, 0 \rangle
→ Finally, the particle is moving right.

✅ Final Observation:

The direction of motion is always tangent to the circle and rotates counterclockwise, consistent with the unit circle’s orientation.

This vector-valued function models uniform circular motion.

Integrals and Motion (Displacement and Distance)

In motion problems, the definite integral of velocity from time a to b gives the displacement. This corresponds to the AP® Calculus AB-BC standard FUN-8.B.2. In contrast, integrating the speed function (the absolute value of velocity) yields the total distance traveled. Therefore, using the “speed formula calculus” is crucial when the path includes changes in direction.

Example (Step-by-Step): Calculating Displacement

1. Suppose v(t) = 2t + 1, and consider t from 0 to 3.
2. The displacement is \int_{0}^{3} v(t) dt = \int_{0}^{3} (2t + 1) , dt.
3. Evaluate the integral:
   • \int (2t + 1) dt = t^2 + t + C
   • Evaluate from 0 to 3: (3^2 + 3) - (0^2 + 0) = 9 + 3 = 12
4. Thus, the particle’s displacement from t = 0 to t = 3 is 12 units.
5. Note that if velocity were negative at any point, one would consider the speed’s absolute value for total distance.

Practice Problem:

Calculate the displacement if v(t) = 4 - t from t = 1 to t = 5.

Set up the integral \int_{1}^{5} (4 - t) dt.

Find the antiderivative: \int (4 - t) dt = 4t - \tfrac{t^2}{2} + C.

Evaluate from 1 to 5:

• For t = 5: 4(5) - (5^2)/2 = 20 - 12.5 = 7.5.
• At t = 1: 4(1) - (1^2)/2 = 4 - 0.5 = 3.5.

Subtract to find the net displacement: 7.5 - 3.5 = 4.

Quick Reference Chart

Term	Definition
Velocity	The rate of change of position; the derivative of the position function, often denoted v(t).
Speed	The magnitude of velocity; speed is always nonnegative.
Acceleration	The rate of change of velocity; the derivative of v(t), often denoted a(t).
Particle at Rest	When v(t) = 0.
Change of Direction	Occurs when velocity changes sign (from positive to negative or vice versa).
Displacement	The net change in position over an interval, given by the definite integral of velocity.
Total Distance Traveled	The integral of speed over an interval; always larger or equal to the displacement.

Conclusion

In summary, a solid understanding of derivatives and integrals makes it easier to answer “When is a particle at rest?” and “When does a particle change direction?” The derivative of position, known as velocity, determines both rest (when v(t) = 0) and direction changes (when v(t) switches sign). Meanwhile, the integral of velocity or speed reveals displacement and total distance traveled. These ideas align closely with AP® Calculus AB-BC objectives FUN-8.B.1 and FUN-8.B.2. Therefore, using instantaneous velocity calculus and speed formula calculus helps accurately describe a particle’s path. By connecting velocity, acceleration, and integrals, one can build a complete picture of motion that is central to many real-world applications.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.