Many real-world situations involve repeated multiplication by a constant factor. This pattern appears in money growth, population modeling, and other areas of study. Therefore, it is vital to understand geometric series, especially the sum of infinite geometric series. A geometric series has each term multiplied by the same constant ratio to get the next term.
This article focuses on the sum of infinite geometric series. This concept is a key topic in AP® Calculus AB-BC and helps students prepare for advanced studies. It also shows how certain repeating processes can converge to a single value. By the end, there should be confidence in using the formula for an infinite geometric series to solve problems quickly.
What We Review
What Is a Geometric Series?
A geometric series is a sequence of numbers in which each term is found by multiplying the previous term by a common factor. This factor is called the common ratio, represented by r. For example, if the first term is a and the common ratio is r, then the terms look like: a, ar, ar^2, ar^3, ...
When these terms are added, the result is a geometric series: a + ar + ar^2 + ar^3 + ...
A finite geometric series has a limited number of terms. An infinite geometric series continues forever. In calculus, infinite series are essential for understanding convergence and divergence. They help students explore ideas such as power series and more advanced topics.
Conditions for Convergence
An infinite geometric series converges only if its common ratio satisfies the condition |r| < 1. In other words, the absolute value of r must be less than 1.
However, if |r| \ge 1, the terms never settle towards a finite value. They either continue growing or fail to approach zero if r is larger than or equal to 1 in magnitude. Therefore, always check the common ratio’s absolute value before applying the sum of infinite geometric series formula.
When |r| < 1, the terms get smaller in magnitude and approach zero. Thus, the infinite sum converges to a particular number, which can be calculated. This observation allows students to see that an ever-decreasing quantity can add up to a finite limit.
The Formula for an Infinite Geometric Series
When the series converges, the sum of infinite geometric series is found using the formula for an infinite geometric series:
S = \frac{a}{1 - r}Here:
- a = first term of the series
- r = common ratio (with |r| < 1)
This formula can be derived by examining partial sums. Each partial sum gets closer to the final limit. Eventually, the infinite series settles to \frac{a}{1 - r} if |r| < 1. Remember to verify that the ratio meets the convergence condition. The image below provides a visual for the proof for the formula for the partial sums.
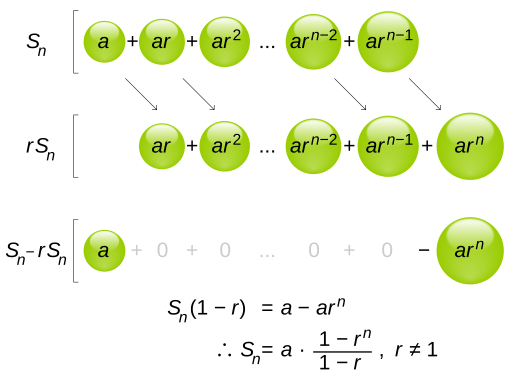
Step-by-Step Examples
Example 1
Suppose the series is 2 + 1 + \frac{1}{2} + \frac{1}{4} + ....
- Identify a and r.
- The first term a = 2.
- The second term is 1, so r = \frac{1}{2}.
- Check for convergence.
- Since |r| = \frac{1}{2} < 1, the series converges.
- Apply the formula for an infinite geometric series: S = \frac{a}{1 - r}.
- Here, a = 2 and r = \frac{1}{2}.
- Calculate the sum: S = \frac{2}{1 - \frac{1}{2}} = \frac{2}{\frac{1}{2}} = 4 .
Hence, the sum of this infinite geometric series is 4.
Example 2
Consider the series 3 - \frac{3}{2} + \frac{3}{4} - \frac{3}{8} + ....
- Determine a and r.
- The first term a = 3.
- To find r, notice that the second term is -\frac{3}{2}. Thus, r = \frac{- \frac{3}{2}}{3} = -\frac{1}{2}.
- Check for convergence.
- |r| = \left| -\frac{1}{2} \right| = \frac{1}{2} < 1, so it converges.
- Use the formula S = \frac{a}{1 - r}.
- Here, a = 3 and r = -\frac{1}{2}.
- Find the sum: S = \frac{3}{1 - \left(-\frac{1}{2}\right)} = \frac{3}{1 + \frac{1}{2}} = \frac{3}{\frac{3}{2}} = 2 .
Therefore, the sum of this infinite series is 2.
Common Mistakes and How to Avoid Them
- Mixing up terms vs. ratio: It is crucial to correctly identify the first term a and the ratio r. Therefore, check the series carefully before applying the formula.
- Forgetting to check |r| < 1: Always confirm convergence. If |r| \ge 1, the series does not converge, and the formula for an infinite geometric series is not valid.
- Misapplication of the sum formula: The sum formula only works for infinite series that satisfy |r| < 1. Thus, do not use it for any other types of series.
Quick Reference Chart
| Vocabulary | Definition |
| Term | A single value in the sequence. For a geometric sequence, each term is found by multiplying the previous term by the common ratio. |
| Common Ratio (r) | The constant factor used to get from one term to the next. |
| Convergence | Occurs when an infinite series approaches a finite value. |
| Partial Sum | The sum of a finite number of terms in the series. As the number of terms grows, the partial sum may approach a limit. |
| Infinite Series | A sum of an unlimited number of terms arranged according to a specific pattern or rule. |
Conclusion
The sum of infinite geometric series can be quickly found using S = \frac{a}{1 - r}, provided that |r| < 1. This requirement ensures that the terms get smaller and converge to a catch-all limit. These ideas are indispensable throughout AP® Calculus AB-BC, especially when working with series and analyzing functions.
Further practice helps solidify mastery. Therefore, it is wise to explore more examples and confirm a solid understanding of the formula. This foundation will provide a head start for tackling more advanced problems in calculus, where infinite series appear in many forms.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








