Understanding when a series diverges can be a huge help in an AP® Calculus AB-BC course. Many series in advanced math can seem mysterious, yet techniques such as the nth term test for divergence provide clarity. This divergence test checks whether the terms of a series approach zero, a basic requirement for possible convergence. This article will explain the key points behind the nth term test for divergence, show how it relates to other tests, and offer step-by-step practice examples.
What We Review
Understanding the Nth Term Test for Divergence
The nth term test for divergence states that if the limit of the nth term a_n of a series is not zero, the series must diverge. Put another way, if: \lim_{n \to \infty} a_n \neq 0, then the series\sum a_n cannot converge.
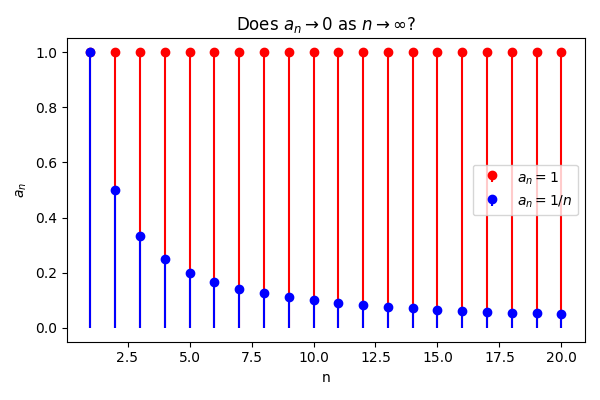
This divergence test is critical because a convergent series needs its terms to shrink toward zero. If they do not, there is no chance for the sum to settle at a finite value. However, a small warning is necessary: even if the limit of a_n is zero, the series might still diverge. Therefore, the nth term test for divergence is a quick way to confirm divergence but is never enough to confirm convergence.
How the Test Applies to Different Series
There are many types of series where the nth term test for divergence can be applied. For instance, consider series where:
- The terms approach a non-zero constant
- The terms oscillate and fail to settle near zero
- The term limit is an obvious non-zero value or undefined
However, remember common pitfalls:
- Zero limit does not imply a convergent series. The harmonic series \sum \frac{1}{n}, for example, has terms that go to zero, yet it diverges.
- The nth term test for divergence can confirm a series is divergent when the term limit is non-zero, but more tests (comparison test, integral test, and others) are required for convergence checks.
Hence, the nth term test for divergence is powerful as a first step. If the limit of a_n is not zero, there is no need to apply other methods because the series diverges.
Step-by-Step Examples
4.1 Example 1
Consider the series \sum 3. Each term in this series is a_n = 3.
- Write down the term:
- a_n = 3.
- Check the limit of a_n as n \to \infty:
- \lim_{n \to \infty} 3 = 3.
- Compare the limit to zero:
- Since 3 \neq 0, the limit of a_n is not zero.
- Conclude divergence:
- By the nth term test for divergence, \sum 3 diverges.
Therefore, a constant (non-zero) term will never yield a convergent series. This example demonstrates how straightforward the divergence test can be.
4.2 Example 2
Next, consider the series \sum \frac{2}{n}. At first glance, the terms \frac{2}{n} tend to zero as n grows large. However, the nth term test for divergence can still provide insight.
- Write down the general term:
- a_n = \frac{2}{n}.
- Evaluate the limit of a_n as n \to \infty:
- \lim_{n \to \infty} \frac{2}{n} = 0.
- Interpret the result:
- Even though this limit equals zero, the nth term test for divergence states only that if the limit is non-zero, the series diverges. It does not claim that if the limit is zero, the series converges.
- Recognize a potential pitfall:
- The series \sum \frac{2}{n} is similar in form to the harmonic series, \sum \frac{1}{n}, which diverges.
- Conclude further tests are necessary:
- Since \lim_{n \to \infty} a_n = 0, the nth term test for divergence cannot confirm divergence, but other tests (like the Comparison Test or p-Series Test) show that \sum \frac{2}{n} indeed diverges.
This example makes it clear that a zero limit is a necessary condition for convergence, but not a sufficient one.
Further Insights and Common Questions
Some students wonder why this divergence test does not guarantee convergence when the terms go to zero. The reason is that terms going to zero only prevent a series from diverging by default. However, there are series with infinitely many small terms that still add up to an unbounded sum.
This is why additional tests are valuable. Methods like the Integral Test, Comparison Test, or Ratio Test often determine if a series converges. Meanwhile, the nth term test for divergence is still a wise first check. If \lim_{n \to \infty} a_n \neq 0, there is no need to try further tests because divergence has already been shown.
Quick Reference Table: Vocabulary and Definitions
| Term/Concept | Definition/Key Feature |
| nth Term | The general term a_n that represents the value of the series at the nth position |
| Divergence Test (Nth Term Test for Divergence) | A test stating if \lim_{n \to \infty} a_n \neq 0, then \sum a_n diverges |
| Limit | The value a function or sequence approaches as n becomes very large |
| Convergence | When the sum of all terms in a series settles to a finite number |
| Necessary Condition | A requirement that must be met for a series to possibly converge |
| Sufficient Condition | A stronger condition that guarantees convergence if met |
Conclusion
The nth term test for divergence, sometimes called the divergence test, is an essential tool in analyzing infinite series. It quickly confirms divergence if the terms do not tend to zero. However, zero terms alone do not ensure convergence. Other methods, such as the integral test or comparison test, are often needed for a full analysis. Students who master the nth term test for divergence gain a solid foundation for understanding other series tests in AP® Calculus AB-BC. Consistent practice with different types of series will strengthen the ability to recognize divergence and, later, confirm convergence.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








