Infinite series appear throughout calculus, especially in AP® Calculus AB-BC. They involve adding an infinite number of terms to see if the sum converges to a specific value or diverges to infinity. Therefore, understanding the properties of these series is essential for problem-solving and deeper application. The p-series is one of the most important examples, along with its special case called the harmonic series. Recognizing and applying tests to these series leads to stronger skills for AP® Calculus exams.
What We Review
What is a p-Series?
Definition and General Form
A p-series is any infinite sum of the form \sum_{n=1}^\infty \frac{1}{n^p} where p is a positive real number. The p-test asks whether this sum converges (has a finite value) or diverges (grows forever). It is important because it provides a quick way to check many series that appear in calculus problems.
Convergence Criteria (p > 1 vs. p ≤ 1)
There is a well-known rule for deciding convergence or divergence of a series. If p > 1, it converges. However, if p \leq 1, it diverges.
- When p = 1, the series is called the harmonic series, which diverges.
- When p is just larger than 1 (like 1.0001), it may still look like it grows slowly, yet it converges by the p-series rule.
Example: Determining the Convergence of a p-Series
Consider the p-series:
\sum_{n=1}^\infty \frac{1}{n^{3/2}}Step-by-step solution:
- Identify that p = \frac{3}{2}.
- Notice \frac{3}{2} > 1. By the p-test, this indicates the series converges.
- Conclude that \sum_{n=1}^\infty \frac{1}{n^{3/2}} converges based on the p-rule.
The key reasoning is that since p is greater than 1, the sum has a finite limit.
Exploring the Harmonic Series
Definition of the Harmonic Series
What is a harmonic series? It is the special case of the p-series when p = 1. In other words, the harmonic series is \sum_{n=1}^\infty \frac{1}{n}. It appears in many areas, such as music theory, physics, and mathematics. Because it is such a simple-looking series, it often surprises newcomers when they learn that it does not converge.
Why the Harmonic Series Diverges
The harmonic series diverges because its partial sums grow slowly but never settle on a single finite value. Each additional term, even though it gets smaller, pushes the sum higher. This makes it a boundary case of the p-series, showing that when p = 1, the sum does not converge. The image below provides a visual of what happens as these terms grow by looking at the corresponding function 1/x.
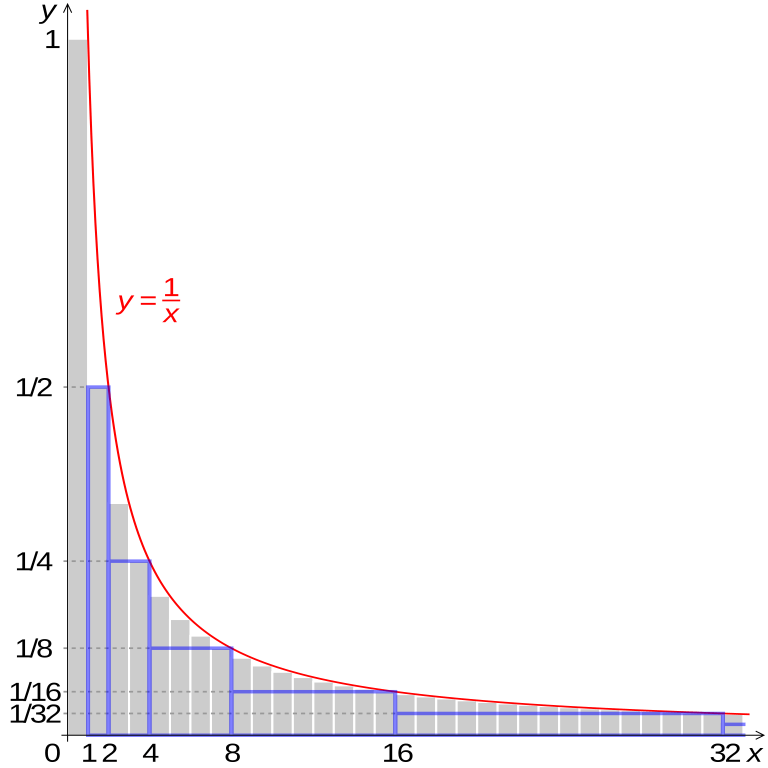
Example: Partial Sums of the Harmonic Series
Consider the partial sums of the harmonic series:
S_k = 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{k}.Step-by-step solution:
- List the first few partial sums:
- S_1 = 1
- S_2 = 1 + \frac{1}{2}
- S_3 = 1 + \frac{1}{2} + \frac{1}{3}
- Observe that each new term adds a positive fraction. Therefore, the sequence of partial sums keeps rising.
- Conclude that the harmonic series diverges because these sums do not approach a finite limit as k goes to infinity.
Comparing p-Series and the Harmonic Series
The p-series rule says that if p > 1, it converges; if p \leq 1, it diverges. The harmonic series (where p = 1) serves as a critical border. On one side of this border, the sum converges, but at this exact boundary, it diverges. Recognizing this distinction is essential on the AP® Calculus exams. Therefore, students often benefit from memorizing the rule and practicing identifying series types quickly.
Quick Reference Chart
Here is a simplified list of important terms and their key features:
| Term | Definition |
| P-series | An infinite sum of the form \sum_{n=1}^\infty \frac{1}{n^p}. |
| P-series Rule | If p > 1, then \sum_{n=1}^\infty \frac{1}{n^p} converges. If p \leq 1, it diverges. |
| Harmonic Series | The special case of the p-series when p = 1. Written as \sum_{n=1}^\infty \frac{1}{n}. |
| Diverges | Describes a series whose partial sums increase without bound or do not settle to one finite value. |
Conclusion
Recognizing p-series in the form \sum_{n=1}^\infty \frac{1}{n^p} and applying the p-test are essential skills. The rule ensures a quick classification of convergence by comparing p to 1. Additionally, the harmonic series diverges as a boundary case, illustrating that p = 1 always leads to an infinite sum. Developing a firm grasp of these concepts lays a strong foundation for success in AP® Calculus and future mathematical studies.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








