Comparison tests are essential tools in calculus for deciding if a series converges or diverges. In many AP® Calculus AB and BC problems, students encounter infinite series and need strategies to evaluate their behavior. Two powerful methods for this task are the Direct Comparison Test and the Limit Comparison Test. This article focuses on both tests, offering simple explanations and examples to demonstrate how they work. Mastering these comparison tests is especially helpful when preparing for exams and tackling more complex infinite series problems.

Understanding Convergence and Divergence

A series is a sum of infinitely many terms, typically written as \sum_{n=1}^{\infty} a_n. Convergence means that as more terms are added, the series settles on a specific value. Divergence means the sum keeps growing without bound or fails to approach a single number.

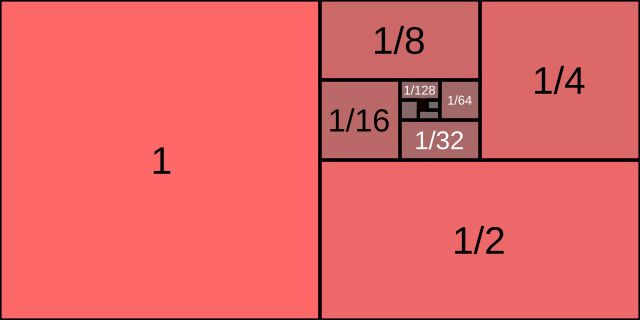
Comparison tests help by matching an unknown series with a known “benchmark” series. If the benchmark series converges (or diverges), and the unknown series has terms smaller (or larger) in a consistent way, the same behavior can be concluded for the unknown series. In other words, the tests use known information to determine whether a new series converges or diverges.

The Direct Comparison Test

Definition and Key Ideas

The Direct Comparison Test works by linking two series through inequalities. Suppose there are two series, \sum_{n=1}^{\infty} a_n and \sum_{n=1}^{\infty} b_n, with non-negative terms. If a_n \leq b_n for all large n and the series \sum b_n converges, then \sum a_n must also converge. Conversely, if a_n \geq b_n and \sum b_n diverges, then \sum a_n will also diverge.

How to Apply the Direct Comparison Test

The Direct Comparison Test usually follows these steps:

• Select a known benchmark series with recognizable behavior (e.g., a p-series \sum \frac{1}{n^p} or a geometric series \sum ar^n).
• Compare each term a_n of the original series with the corresponding term b_n of the known series.
• Establish an inequality like a_n \leq b_n (or a_n \geq b_n) and use the known result (convergence or divergence) of \sum b_n to draw a conclusion.

Example with Step-by-Step Solution

Consider the series \sum_{n=1}^{\infty} \frac{1}{n^2+1}. Determine if it converges or diverges.

• Step 1: Recognize that \frac{1}{n^2+1} is similar to \frac{1}{n^2}.
• Step 2: Note that \frac{1}{n^2+1} \leq \frac{1}{n^2} for all n \ge 1, because adding 1 to n^2 in the denominator makes the fraction smaller.
• Step 3: Recall that \sum_{n=1}^{\infty} \frac{1}{n^2} (a p-series with p=2) converges.
• Step 4: Since \frac{1}{n^2+1} \leq \frac{1}{n^2} and \sum_{n=1}^{\infty} \frac{1}{n^2} converges, the Direct Comparison Test implies \sum_{n=1}^{\infty} \frac{1}{n^2+1} converges as well.

Practice Problem (Direct Comparison Test):

Decide if \sum_{n=1}^{\infty} \frac{1}{2^n} converges or diverges.

Solution:

1. Recognize that \frac{1}{2^n} is part of a geometric series with ratio \frac{1}{2}.
2. Compare to \sum_{n=1}^{\infty} \frac{1}{2^n} itself, which converges by the geometric series test.
3. Using the fact that the ratio is less than 1, the sum converges. Thus, by direct comparison with a known geometric series, \sum_{n=1}^{\infty} \frac{1}{2^n} converges.

The Limit Comparison Test

Introduction to the Limit Comparison Test

When direct inequalities are not obvious, the Limit Comparison Test offers more flexibility. It is often referred to as the series limit comparison test. In this test, two series \sum a_n and \sum b_n (with positive terms) are compared using a limit of their ratio. If the limit exists and is a positive finite number, both series share the same behavior: either both converge or both diverge.

Limit Comparison Test Rules: How It Works

The limit comparison test rules can be summarized as follows:

1. Choose a comparison series \sum b_n with known behavior (convergent or divergent).
2. Compute the limit \lim_{n \to \infty} \frac{a_n}{b_n}.
3. If the limit is a positive finite number (not 0, not \infty), then \sum a_n and \sum b_n either both converge or both diverge.

Example with Step-by-Step Solution

Determine whether
\displaystyle \sum_{n=1}^{\infty} \frac{3}{4n^2 - 1} converges or diverges.

Step 1: Choose a Benchmark Series

We focus on the dominant term in the denominator. Since 4n^2 - 1 \sim 4n^2 for large n, we compare with the convergent p-series:

\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^2}

This is a p-series with p = 2 > 1, which converges.

Step 2: Set Up the Limit Comparison

Let:

• a_n = \frac{3}{4n^2 - 1}
• b_n = \frac{1}{n^2}

Compute:

\lim_{n \to \infty} \frac{a_n}{b_n}= \lim_{n \to \infty} \frac{\frac{3}{4n^2 - 1}}{\frac{1}{n^2}}= \lim_{n \to \infty} \frac{3n^2}{4n^2 - 1}

Step 3: Simplify the Limit

\lim_{n \to \infty} \frac{3n^2}{4n^2 - 1}= \lim_{n \to \infty} \frac{3}{4 - \frac{1}{n^2}}= \frac{3}{4}

Step 4: Conclude Using the Limit Comparison Test

Since:

• The limit \frac{3}{4} is a positive finite number, and
• \sum \frac{1}{n^2} converges,

…we conclude that:
\boxed{\sum_{n=1}^{\infty} \frac{3}{4n^2 - 1} \text{ converges}} by the Limit Comparison Test.

Practice Problem (Limit Comparison Test):

Decide if \sum_{n=1}^{\infty} \frac{n+1}{2n+3} converges or diverges.

Solution:

1. Compare \frac{n+1}{2n+3} to \frac{1}{n}.
2. Consider \lim_{n \to \infty} \frac{\frac{n+1}{2n+3}}{\frac{1}{n}} = \lim_{n \to \infty} \frac{n+1}{2n+3} \cdot n .
3. Simplify: \lim_{n \to \infty} \frac{n(n+1)}{2n+3} = \lim_{n \to \infty} \frac{n^2 + n}{2n + 3}.
   • Divide numerator and denominator by n: \lim_{n \to \infty} \frac{n + 1}{2 + \frac{3}{n}} = \infty.
4. The limit is infinite, which does not fit the “positive finite number” case. Notice that \sum \frac{1}{n} diverges. Because this limit suggests the given terms behave at least as large as \frac{1}{n}, the original series diverges.

When to Use Limit Comparison vs. Direct Comparison

Sometimes, a direct inequality a_n \leq b_n or a_n \geq b_n is clear, so the direct comparison test is quick. However, when straightforward inequalities are not obvious, the limit comparison test rules are more flexible. By examining the ratio of terms, one can determine convergence or divergence even if the terms are complicated.

Additional Considerations

It is important to pick a comparison series that is easy to handle. For instance, a p-series \sum \frac{1}{n^p} is helpful when powers of n are involved, and a geometric series \sum ar^n is best if there is a common ratio. A common pitfall is choosing an inappropriate benchmark, which may lead to misleading comparisons. Therefore, knowing standard convergent series and divergent series is a key step.

Quick Reference Chart

Term/Concept	Definition / Explanation
Direct Comparison Test	Uses inequalities between series terms to conclude convergence or divergence.
Limit Comparison Test	Uses the ratio of terms to a known series to determine convergence or divergence. Applies a “limit” as the deciding factor.
Comparison Series	A simpler series whose behavior (convergent or divergent) is already known, serving as a benchmark.
Convergence	A series converges if its terms add to a finite value as the number of terms increases.
Divergence	A series diverges if it does not approach a finite limit when summing more and more terms.

Conclusion

Comparison tests stand out as effective strategies for determining the fate of complicated infinite series. Through examples and step-by-step solutions, the Direct Comparison Test and the series limit comparison test have been shown to guide students toward clear convergence or divergence conclusions. Consistent practice with these tests is invaluable for success in AP® Calculus AB and BC, as they appear in a range of series problems. With a firm grasp of both the direct approach and the limit comparison test rules, solving infinite series questions becomes significantly more approachable.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.