A series is an infinite sum of terms, such as \sum_{n=1}^{\infty} a_n. If the partial sums of this infinite series settle on a finite value, we say the series converges. However, if these partial sums keep growing without bound or keep oscillating, the series diverges. One common method used to determine this behavior is the ratio test convergence of series, which helps identify whether a series converges or diverges based on the limit of the ratio of successive terms.

Studying convergence is vital because it tells us whether the sum of infinitely many terms has a meaningful result. In AP® Calculus AB-BC, understanding series convergence helps you tackle advanced problems in analysis.

Purpose of the Ratio Test

The ratio test convergence of series is a powerful tool. It examines how consecutive terms compare in size. If these terms shrink fast enough, the series converges. If the terms do not shrink (or even grow), the series diverges.

This approach becomes especially useful when dealing with factorials or exponential expressions. Later, we will see how it fits alongside other methods like the root test for convergence.

Recap: Convergence Tests and Where the Ratio Test Fits

Common Tests for Convergence

Before focusing on the ratio test, remember that there are several tests available: the p-series test, comparison test, integral test, and root test for convergence. Each of these methods is better suited for certain types of series.

Why Use the Ratio Test?

The ratio test often shines with factorials and exponential functions. These types of terms can be hard to compare directly, yet forming a ratio of successive terms often simplifies quickly. Therefore, the ratio test can be more efficient than other techniques. In general, if you see factorials (n!) or powers of n (n^k) combined with exponentials, the ratio test might be your best friend.

How the Ratio Test Works

Ratio Test Rules

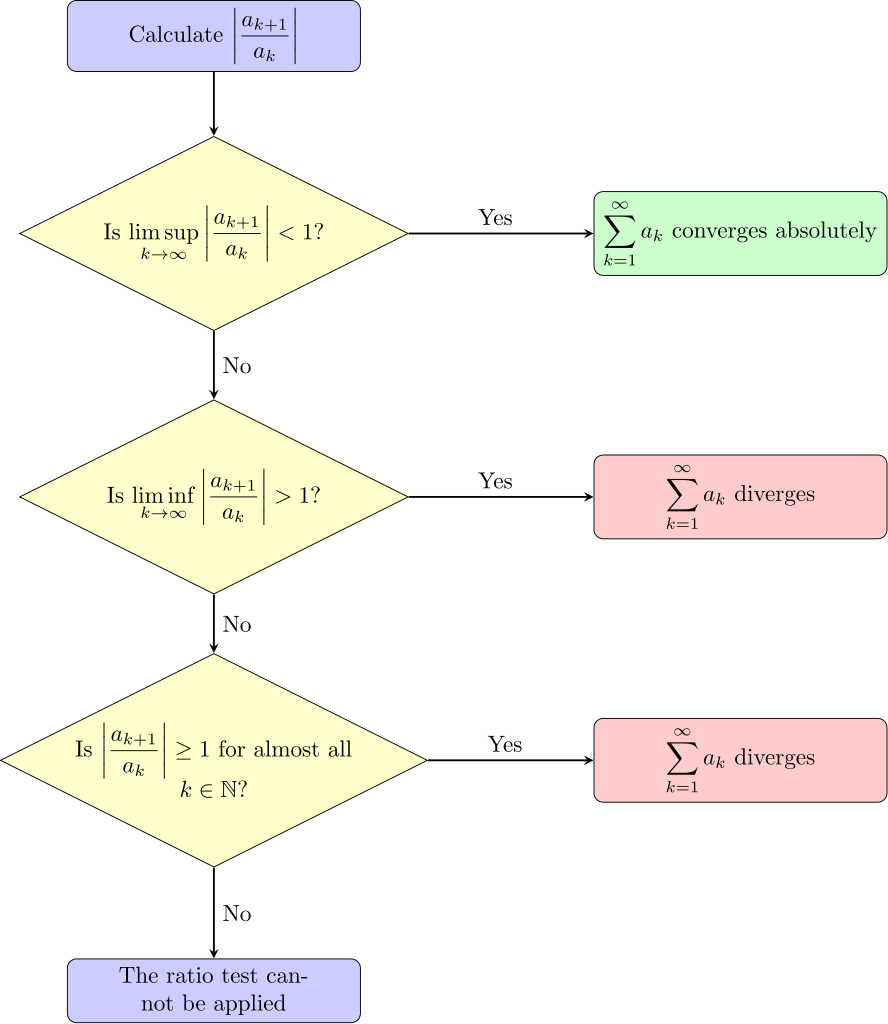
First, consider a general series \sum_{n=1}^{\infty} a_n. Define L as the limit:

L = \lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right|.

Then the ratio test rules say:

• If L < 1, the series converges.
• If L > 1, the series diverges.
• If L = 1, the test is inconclusive.

Step-by-Step Method

1. Identify a_n, the general term.
2. Form the ratio \left|\frac{a_{n+1}}{a_n}\right|.
3. Simplify and find \lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right|.
4. Apply the ratio test rules. Conclude whether the series converges or diverges.

Ratio Test Examples: Step-by-Step Solutions

Example 1: Series Involving Factorials

Consider the series: \sum_{n=1}^{\infty} \frac{n!}{3^n}.

Step-by-Step Solution

1. Write down the general term: a_n = \frac{n!}{3^n}.
2. Form the ratio of the consecutive terms: \left|\frac{a_{n+1}}{a_n}\right|= \frac{\frac{(n+1)!}{3^{n+1}}}{\frac{n!}{3^n}}= \frac{(n+1)!3^n}{n!3^{n+1}}.
3. Simplify: = \frac{(n+1) \cdot n! \cdot 3^n}{n! \cdot 3^n \cdot 3}= \frac{n+1}{3}.
4. Take the limit as n \to \infty: L = \lim_{n \to \infty} \frac{n+1}{3} = \infty , (> 1).
5. Since L > 1, the series diverges by the ratio test rules.

Practice Problem

Determine if the series \sum_{n=1}^{\infty} \frac{n!}{2^n} converges or diverges.

Step-by-Step:

1. a_n = \frac{n!}{2^n}.
2. \left|\frac{a_{n+1}}{a_n}\right|= \frac{\frac{(n+1)!}{2^{n+1}}}{\frac{n!}{2^n}}= \frac{(n+1) \cdot n! \cdot 2^n}{n! \cdot 2^n \cdot 2}= \frac{n+1}{2}.
3. As n \to \infty, \frac{n+1}{2} \to \infty > 1.
4. Therefore, the series diverges by the ratio test convergence of series.

Example 2: Exponential Functions

Now consider the infinite series:\sum_{n=1}^{\infty} \frac{3^n}{4^n}.

Step-by-Step Solution

1. Identify a_n: a_n = \left(\frac{3}{4}\right)^n.
2. Form the ratio: \left|\frac{a_{n+1}}{a_n}\right|= \frac{\left(\frac{3}{4}\right)^{n+1}}{\left(\frac{3}{4}\right)^n}= \frac{3}{4}.
3. Evaluate the limit as n \to \infty: L = \frac{3}{4} < 1.
4. Because L < 1, the series converges by the ratio test.

Practice Problem

Determine whether \sum_{n=1}^{\infty} \left(\frac{2}{3}\right)^n converges or diverges.

Step-by-Step:

1. a_n = \left(\frac{2}{3}\right)^n.
2. \left|\frac{a_{n+1}}{a_n}\right|= \frac{\left(\frac{2}{3}\right)^{n+1}}{\left(\frac{2}{3}\right)^n}= \frac{2}{3}.
3. L = \frac{2}{3} < 1.
4. By the ratio test rules, the series converges.

Connect to the Root Test for Convergence

When to Consider the Root Test Instead

Sometimes, applying the ratio test can get messy. If you find yourself with complicated exponents or nth powers that do not simplify easily, the root test for convergence might be simpler. The root test involves evaluating \lim_{n \to \infty} \sqrt[n]{|a_n|}, which can handle certain types of series more smoothly.

Similarities and Differences

Both methods aim to measure how terms behave as n becomes large. However, the ratio test looks at \frac{a_{n+1}}{a_n}, whereas the root test involves \sqrt[n]{|a_n|}. They often agree on convergence or divergence, but each approach may be more straightforward for specific problems.

Common Pitfalls and Tips

Watch for Complex Expressions

Factors like n! or mixed terms (n^k \cdot e^n) require careful simplification. Therefore, rewrite expressions fully before taking the limit. Make sure common parts cancel out neatly.

Inconclusive Case

If you get L = 1, the ratio test rules do not help. In this scenario, consider other tests such as the root test for convergence or the comparison test. This extra step often avoids a wrong conclusion.

VII. Quick Reference Chart

Term	Definition
Convergence of a Series	When the partial sums of an infinite series approach a finite limit.
Ratio Test	A method that examines the limit of the ratio of consecutive terms to determine series convergence.
Ratio Test Rules	If the limit of |a_{n+1} /a_n| < 1, the series converges; > 1, it diverges; = 1, the test is inconclusive.
Root Test for Convergence	Uses the nth root of |aₙ| to determine if a series converges or diverges.

Conclusion

The ratio test convergence of series is an efficient way to determine whether an infinite series converges or diverges. It relies on checking the limit of consecutive term ratios. If that limit is less than one, the series converges; if greater than one, it diverges; and if equal to one, you need a different test.

Keep these ratio test rules on hand, and practice using them with various series. If you get stuck with the ratio test, try the root test for convergence or other methods. Exploring different examples will deepen understanding and build confidence for AP® Calculus AB-BC and beyond.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.