Alternating series appear frequently in AP® Calculus AB-BC, especially when dealing with infinite sums that switch signs term by term. Therefore, it is essential to know how to gauge if these series converge and how far a partial sum might be from the true value. The alternating series error bound serves as a powerful tool in this process.

Having a clear grasp of the alternating series estimation theorem helps when estimating sums without computing every term. Next, this article explores the key definitions, theorems, and strategies for handling these intriguing series. It concludes with user-friendly examples and a quick reference chart.

Key Definitions and Concepts

Recap of the Alternating Series Test

An alternating series switches between positive and negative terms. For instance, a series with general term (-1)^n a_n has terms that alternate in sign. The Alternating Series Test states that if:

• a_n \geq 0,
• a_{n+1} \leq a_n (terms decrease in absolute value), and
• \lim_{n\to\infty} a_n = 0,

then the series \sum_{n=1}^{\infty} (-1)^n a_n converges.

Introducing the Alternating Series Error Bound Formula

When determining how accurate a partial sum is, the alternating series error bound formula becomes essential. This formula indicates that the error in approximating an alternating series is at most the next omitted term in absolute value. Textbooks might write it as: |R_N| \leq a_{N+1}, where R_N is the remainder (error) after summing N terms.

The Alternating Series Estimation Theorem

The alternating series estimation theorem provides a precise way to measure the difference between a partial sum and the series’ true value. Specifically, it helps predict how large the error may be.

Statement of the Theorem

According to the theorem, if the conditions of the Alternating Series Test are satisfied, then the magnitude of the error when using the partial sum S_N is at most a_{N+1}. This result is valuable for quick approximations, because just one term beyond N is enough to bound the error.

Conditions for Using the Theorem

The series must have terms that decrease in absolute value. Additionally, each term must approach zero as n goes to infinity. Therefore, always check that a_n decreases monotonically and that \lim_{n\to\infty} a_n=0.

Connecting the Theorem to the Error Bound Formula

After confirming the conditions, the alternating series error bound formula applies:

|S - S_N| \leq a_{N+1}.

Here, S is the actual sum of the infinite series, while S_N represents the partial sum after N terms. Therefore, the first omitted term controls the maximum possible error.

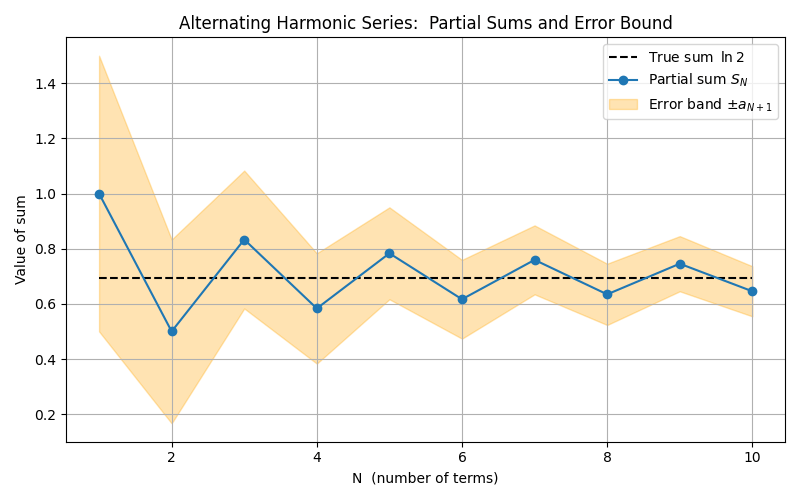
Example 1: Applying the Alternating Series Error Bound

Problem Statement

Consider the series:

\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n}.

Find the error bound after summing the first four terms and explain how it relates to the true sum.

Step-by-Step Solution

1. Check Conditions:
   • The terms are \frac{1}{n} in absolute value, which decrease as n gets larger.
   • The limit of 1/n is zero. Hence, the conditions of the Alternating Series Test are satisfied.
2. Identify the Next Term:
   • After four terms, the next term is \frac{1}{5} in absolute value.
3. Apply the Alternating Series Estimation Theorem:
   • The alternating series error bound formula indicates the error is at most \frac{1}{5}.
   • Thus, |R_4| \le \frac{1}{5}.
4. Conclusion:
   • The partial sum using four terms is within \frac{1}{5} of the series’ true sum.
   • This quick check shows the sum approximation is reasonably close even with only a few terms.

Practical Strategies for Using the Error Bound

Calculus questions often expect quick application of the alternating series error bound. The following strategies simplify the process:

• Quickly verify that a_n is decreasing. Examine whether a_{n+1} \le a_n.
• Always check \lim_{n\to\infty} a_n = 0. If it is nonzero, the test cannot be used.
• Decide how many terms are needed based on the desired accuracy. For instance, if a problem demands an error less than 0.001, keep adding terms until the next term is under 0.001.

Exam-style questions frequently involve specifying how many terms to use. Therefore, practice identifying the term size needed to ensure a particular level of accuracy.

Example 2: More Complex Series With Alternating Series Error Bound

Problem Statement

Consider the series:

\sum_{n=1}^{\infty} (-1)^{n+1} \frac{\sqrt{n}}{n+1}.

Determine how many terms are required to ensure the error is below 0.05. Then, use the partial sum of that many terms to approximate the series.

Step-by-Step Solution

1. Check Monotonic Decrease:
   • Note that a_n = \frac{\sqrt{n}}{n+1} must decrease in n.
   • Compare a_n and a_{n+1}. For large n, \sqrt{n} grows slower than n+1, so a_n tends to decrease.
2. Find the Number of Terms for Desired Accuracy:
   • Use the alternating series estimation theorem and set a_{N+1} < 0.05.
   • Solve \frac{\sqrt{N+1}}{(N+1)+1} < 0.05.
   • Check integer values to find the smallest N satisfying this inequality.
3. Compute the Partial Sum:
   • Once N is determined, add the terms \frac{\sqrt{1}}{1+1}, -\frac{\sqrt{2}}{2+1}, \frac{\sqrt{3}}{3+1}, \dots up to N terms.
   • This partial sum is within 0.05 of the true value.
4. Interpret the Result:
   • Conclude that including enough terms to make a_{N+1} < 0.05 ensures the error bound is satisfied.
   • Therefore, the approximation meets the desired accuracy.

Practice Problem

Use the alternating series error bound formula on the series: \sum_{n=1}^{\infty} \frac{(-1)^n}{n^2}.

1. Determine whether the conditions of the Alternating Series Test are met.
2. Find how many terms are needed so that the error is less than 0.01.
3. Show your calculation steps and evaluate the partial sum for that many terms.

Practice Problem Solution (Step-by-Step)

1. Conditions Check:
   • a_n = \frac{1}{n^2}, which decreases as n increases and approaches zero.
2. Number of Terms for \varepsilon=0.01:
   • Require \frac{1}{(N+1)^2} < 0.01.
   • Solve (N+1)^2 > 100, so N+1 > 10. Thus, N > 9.
3. Compute Partial Sum:
   • Sum the first 10 terms of \frac{(-1)^n}{n^2}. The error will be at most \frac{1}{(10+1)^2} = \frac{1}{121} \approx 0.0083, which is under 0.01.
4. Conclusion:
   • After 10 terms, the error is below 0.01, meeting the requirement.

Quick Reference Chart: Vocabulary and Definitions

Term or Phrase	Definition or Explanation
Alternating Series	A series whose terms alternate in sign (positive, negative, etc.).
Alternating Series Test	A test stating that if terms decrease in absolute value and approach zero, then the series converges.
Alternating Series Error Bound	A way to estimate the difference between a partial sum and the true value of an alternating series.
Alternating Series Estimation Theorem	The theorem specifying that the maximum error is at most the next omitted term in absolute value.
Monotonic Decrease	A sequence in which each term is less than or equal to the previous term.
Infinite Series	The sum of infinitely many terms, which may or may not converge to a specific value.

Conclusion

The alternating series error bound is a critical concept in AP® Calculus AB-BC for analyzing the accuracy of partial sums. Checking that terms decrease in absolute value and tend to zero is the first step before applying the bound. Then, the alternating series estimation theorem keeps the process quick and consistent.

Students are encouraged to practice identifying conditions, applying the alternating series error bound formula, and interpreting results. Exam questions often focus on estimating how many terms are necessary for a desired level of precision. Therefore, solidifying these skills ensures confidence in tackling alternating series questions and beyond.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.