Radius and interval of convergence play a key role in understanding how series and power series behave. When a function is written as a power series, it can only converge in certain regions around its center. Therefore, identifying that region ensures the series can be used reliably in calculations or approximations.

Key terms to keep in mind include “power series,” “radius of convergence,” and “interval of convergence.” These terms will appear frequently in the analysis of convergence.

These concepts align closely with the AP® Calculus AB-BC curriculum, especially standards LIM-8.D.1 through LIM-8.D.6. Therefore, a solid grasp of the radius and interval of convergence supports a deeper understanding of Taylor series and their convergence properties. Indeed, these tools help when verifying whether certain approximations stay accurate within specific ranges.

Understanding Power Series

Definition of a Power Series

A power series is a sum of terms that involve powers of a variable centered at some point. The general form can be written as:

\sum_{n=0}^{\infty} a_n (x - r)^n

Here, r is called the center, and the a_n values are the coefficients. It helps to think of it like a polynomial with infinitely many terms, yet it only behaves like a finite polynomial in certain ranges of x.

Why Convergence Matters

Not every power series converges for all x values. Instead, convergence can happen only at a single point, over an interval, or possibly for all real numbers. Therefore, knowing where the series converges ensures that any function values or approximations derived from it are valid.

Example: Finding a Specific Power Series

Consider the series:

\sum_{n=0}^{\infty} \frac{x^n}{n!}

It is a simple example because a_n = \frac{1}{n!} and r = 0. This means the series is centered at 0.

Step-by-Step Explanation

1. Observe that the general term is \frac{x^n}{n!}.
2. Notice the center r=0, so the series appears as x^n terms divided by n!.
3. This series actually converges for all real x. This fact can be shown by using the ratio test, which will appear in the next section.

The Radius of Convergence

Role of the Ratio Test

A popular way to determine the radius of convergence is the ratio test (AP® standard LIM-8.D.3). The ratio test compares the sizes of consecutive terms. If the ratio approaches a value less than 1, the series converges; if it is greater than 1, the series diverges.

Here is the ratio test for a general term a_n:

\lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right|

• If this limit is less than 1, the series converges.
• If it is greater than 1, the series diverges.
• If it equals 1, the test is inconclusive.

Computing the Radius of Convergence

When applying this test to a power series \sum_{n=0}^{\infty} a_n (x - r)^n, one formula often emerges:

R = \frac{1}{\lim_{n\to\infty} \left|\frac{a_{n+1}}{a_n}\right|},

…as long as the limit exists. This expression is sometimes referred to as the “radius of convergence calc” because it directly calculates the radius R in which the series behaves nicely.

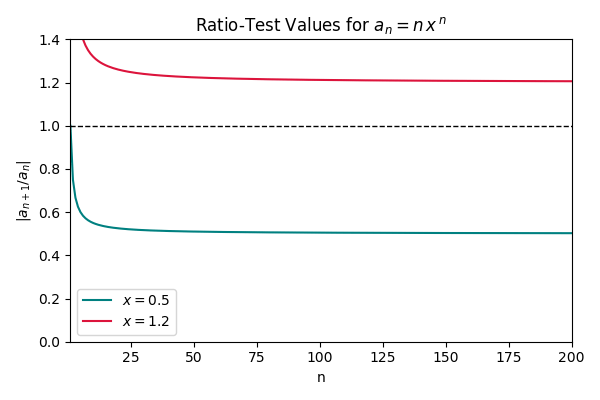
Example: Applying the Ratio Test

Consider the series:

\sum_{n=1}^{\infty} n x^n

Step-by-Step Ratio Test Solution

1. The n^{\text{th}} term is a_n = n x^n.
2. Apply the ratio test: \lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right| = \lim_{n \to \infty} \left|\frac{(n+1)x^{n+1}}{n x^n}\right|.
3. Simplify inside the limit: = \lim_{n \to \infty} \left|\frac{n+1}{n}\right| \cdot |x| = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right) |x|= 1 \cdot |x| = |x|.
4. For convergence, require |x| < 1. Hence, the radius of convergence here is R = 1.

The image below shows two values of x for the series and what happens as n increases.. One is inside the radius of convergence, and one is outside.

The Interval of Convergence

Using the Radius to Find the Interval

Once the radius of convergence R is found, the interval of convergence can be written as:

|x - r| < R.

This is an open interval. However, to confirm the exact interval, it is crucial to test the endpoints r + R and r - R (AP® standard LIM-8.D.4). These endpoints might converge or diverge, changing the final answer.

How to Find Interval of Convergence

To see how to find interval of convergence in a step-by-step manner:

• Identify R from the ratio test.
• Check x = r + R and x = r - R separately.
• Use appropriate tests (like the alternating series test, p-series test, or direct comparison) to see if the series converges.
• Include or exclude the endpoints based on the results.

Example: Checking Convergence at Endpoints

For a power series \sum_{n=0}^{\infty} \frac{x^n}{n+1}, assume it is centered at 0 and the ratio test yields R = 1. Then the candidate interval is -1 < x < 1.

Step-by-Step Endpoint Check

1. Test at x = 1:
   • The series becomes \sum_{n=0}^{\infty} \frac{1^n}{n+1} = \sum_{n=0}^{\infty} \frac{1}{n+1}.
   • This is the harmonic series (shifted index), which diverges.
2. Test at x = -1:
   • The series becomes \sum_{n=0}^{\infty} \frac{(-1)^n}{n+1}.
   • This converges (by the alternating series test).

So, the interval of convergence is -1 \le x < 1.

Effects of Differentiation and Integration on Convergence

Term-by-Term Operations

A useful theorem states that differentiating or integrating a power series term by term does not change its radius of convergence (AP® standard LIM-8.D.6). Therefore, the radius remains the same, although interval endpoints may still need checking to see if they behave differently after differentiation or integration.

Example: Simple Term-by-Term Differentiation

Consider \sum_{n=0}^{\infty} x^n, which converges for |x| < 1. The derivative is:

\sum_{n=1}^{\infty} n x^{n-1}.

The radius of convergence is still 1. Testing endpoints might yield different results, but R remains the same.

Step-by-Step Confirmation

1. Original series: \sum_{n=0}^{\infty} x^n = \frac{1}{1 - x}, valid for |x| < 1.
2. Differentiate term by term: \frac{d}{dx} \left(\sum_{n=0}^{\infty} x^n\right) = \sum_{n=1}^{\infty} n x^{n-1}.
3. The ratio test on the new series leads to the same radius, R = 1.

Quick Reference Chart: Important Vocabulary

Term	Definition
Power Series	An infinite sum of terms a_n(x - r)^n.
Radius of Convergence	The distance R from the center where the series converges.
Interval of Convergence	The set of x values for which the series converges, often determined by |x - r< R plus endpoint checks.
Ratio Test	A test using \lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right| to determine convergence.
Endpoint Convergence	Checking whether a series converges or diverges at x = r \pm R.

Conclusion

Key Takeaways

Radius and interval of convergence provide the foundation for working with power series. Therefore, testing where a series converges allows accurate computations and supports deeper topics like Taylor series. Indeed, whether the goal is to perform a radius of convergence calc or to see how to find interval of convergence, the key steps involve knowing R and checking endpoints carefully.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.