Introduction

On the SAT® Math section, questions about systems of equations appear often. Sometimes the two equations are both lines. Other times, one or both equations curve—think parabolas, circles, or radicals. Because each system represents where two graphs meet, knowing how to solve nonlinear system of equations​ quickly unlocks multiple points on test day. This guide explores the difference between linear and nonlinear systems and presents reliable strategies such as substitution, elimination, and smart graph reading. By the end, expect to recognize when a system has zero, one, or two real solutions and to avoid common SAT® traps.

Foundations: What Is a “System” of Equations?

A system is a set of two or more equations with the same variables. A solution set is any ordered pair that satisfies all equations simultaneously. Picture two roads on a map. The point where they cross is the shared solution. If they never cross, there is no solution. That road‐map image carries through every method in this guide.

Quick Diagnostic Warm-Up

Solve in under 2 minutes:

\begin{cases} 3x + 2y = 14 \\ y = 2x - 1\end{cases}

Step	Reason
\begin{cases} 3x + 2y = 14 \\ y = 2x - 1\end{cases}	Original system of equations
3x + 2(2x - 1) = 14	Substitute y = 2x - 1 into the first equation
3x + 4x - 2 = 14	Distribute latex]2latex]2 to both terms
7x = 16	Combine like terms and add latex]2latex]2 to both sides
x = \dfrac{16}{7}	Divide both sides by 7
y = 2\left(\dfrac{16}{7}\right) - 1 = \dfrac{32}{7} - \dfrac{7}{7} = \dfrac{25}{7}	Substitute x into y=2x−1

If this felt smooth, great—keep reading for harder twists. If it felt shaky, the coming sections will shore up every step.

Solving Linear Systems

Substitution Method

1. Isolate one variable in either equation.
2. Substitute into the other equation.
3. Solve for one variable, then back-solve for the other.

Example

\begin{cases} y = 5 - 3x \\ 2x + y = -1 \end{cases}

Step	Reason
\begin{cases} y = 5 - 3x \\ 2x + y = -1 \end{cases}	Original system of equations
2x + (5 - 3x) = -1	Substitute y=5−3x into the second equation
-x + 5 = -1	Combine like terms
x = 6	Solve for latex]x[/latex]
y = 5 - 3(6) = -13	Back-substitute x=6 into y=5−3x

Elimination Method

1. Multiply one or both equations so coefficients of one variable match.
2. Add or subtract to eliminate.
3. Solve for the remaining variable.

Example

\begin{cases} 4x - y = 9 \\ 6x + 2y = 4 \end{cases}

Step	Reason
\begin{cases} 4x - y = 9 \\ 6x + 2y = 4 \end{cases}	Original system of equations
2(4x - y) = 2(9) \Rightarrow 8x - 2y = 18	Multiply the first equation by 2 to align terms
(6x + 2y) + (8x - 2y) = 4 + 18	Add equations to eliminate y
14x = 22	Simplify
x = \dfrac{11}{7}	Solve for x
4\left(\dfrac{11}{7}\right) - y = 9	Substitute x = \dfrac{11}{7} into the first equation
\dfrac{44}{7} - y = 9 \Rightarrow -y = 9 - \dfrac{44}{7} = \dfrac{19}{7}	Solve for y
y = -\dfrac{19}{7}	Final solution for y

Graphing Method

Sometimes the SAT® gives the graph or asks only for the number of solutions. When two lines:

• Intersect once → one solution.
• Are parallel but distinct → no solution.
• Are coincident (same line) → infinitely many solutions.

Mental-math tip: Compare slopes. Equal slopes but different intercepts mean no intersection, so answer quickly without algebra.

Linear–Quadratic Systems

A line and a parabola can meet 0, 1, or 2 times.

Example

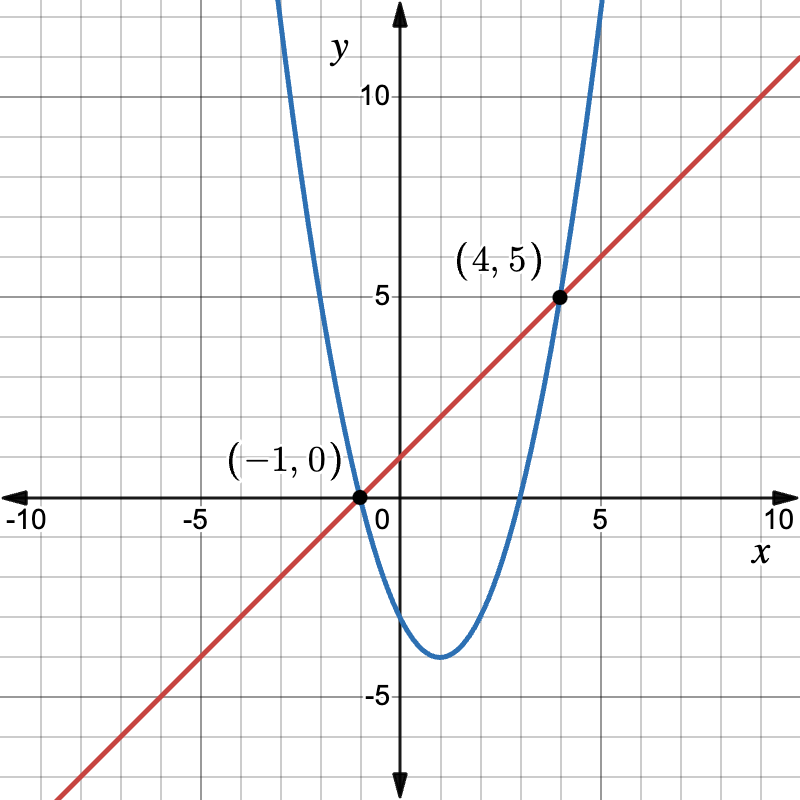
\begin{cases} y = x + 1 \\ y = x^{2} - 2x - 3 \end{cases}

Step	Reason
x + 1 = x^2 - 2x - 3	Original equation
0 = x^2 - 2x - 3 - x - 1	Subtract x+1 from both sides
0 = x^2 - 3x - 4	Combine like terms
(x - 4)(x + 1) = 0	Factor the quadratic
x = 4 \quad \text{or} \quad x = -1	Solve using the Zero Products Property ✅

Find y-values using the line:

• If x = 4, then y = 5.
• If x = -1, then y = 0.

The solutions are (4,5) and (-1,0).

Graphically, confirm the parabola opens upward while the line cuts through twice.

Quadratic–Quadratic Systems

When both equations curve, elimination by subtraction often works best.

Example

\begin{cases} x^2 + y^2 = 23 \\ y = x^2 - 3 \end{cases}

Step	Reason
\begin{cases} x^2 + y^2 = 23 \\ y = x^2 - 3 \end{cases}	Original system of equations
x^2 + (x^2 - 3)^2 = 23	Substitute the parabola into the circle
x^2 + (x^4 - 6x^2 + 9) = 23	Expand the squared binomial
x^4 - 5x^2 + 9 = 23	Combine like terms
x^4 - 5x^2 - 14 = 0	Subtract 23 from both sides
Let u=x^2: u^2 - 5u - 14 = 0	Use substitution to create a quadratic
u = \dfrac{5 \pm \sqrt{25 + 56}}{2} = \dfrac{5 \pm \sqrt{81}}{2}	Apply the quadratic formula
u = \dfrac{5 \pm 9}{2}	Simplify the square root
u = 7\ \text{or}\ u = -2	Solve for u
x^2 = 7 \Rightarrow x = \pm\sqrt{7}; \\ x^2 = -2 \Rightarrow \text{reject (no real roots)}	Find real x-values
y = x^2 - 3 = 7 - 3 = 4	Substitute x^2 = 7 into the parabola equation

Intersections: \left(\pm\sqrt{7},4\right).

Absolute Value Systems

Absolute value graphs form “V” shapes. Splitting into cases turns the system into piecewise linear equations.

Example

\begin{cases} |y - 3| = 2x \\ y = x + 1 \end{cases}

There are two cases:

Case 1: y - 3 = 2x

Case 2: y-3 = -2x

Step	Reason
\begin{cases} y - 3 = 2x \\ y = x + 1 \end{cases}	Original system for Case 1
(x + 1) - 3 = 2x	Substitute y=x+1 into the first equation
x - 2 = 2x	Simplify
-2 = x \Rightarrow x = -2	Solve for x
y = -2 + 1 = -1	Back-substitute to find y

Step	Reason
\begin{cases} y - 3 = -2x \\ y = x + 1 \end{cases}	Original system for Case 2
(x + 1) - 3 = -2x	Substitute y=x+1 into the first equation
x - 2 = -2x	Simplify
3x = 2 \Rightarrow x = \dfrac{2}{3}	Solve for x
y = \dfrac{2}{3} + 1 = \dfrac{5}{3}	Back-substitute to find y

Solutions: (-2,-1) and \left(\dfrac{2}{3},\dfrac{5}{3}\right).

On a graph, those are the two intersection points between the “V” and the line.

Radical & Rational Systems and Extraneous Solutions

Radicals and fractions may introduce solutions that disappear when checked against originals.

Example

\begin{cases} \sqrt{y} = x + 1 \\ y = x^{2} \end{cases}

To solve the system, follow these steps:

• Substitute x^2 in for y in the first equation: \sqrt{x^2} = x + 1
• Since \sqrt{x^2} = |x|, rewrite the equation as: |x| = x + 1

Now solve using cases:

Case 1: x \ge 0

• |x| = x, so the equation becomes: x = x + 1, which leads to 0 = 1
• This is not possible, so there is no solution in this case.

Case 2: x < 0

• |x| = -x, so the equation becomes: -x = x + 1
• Solving: 2x = -1 → x = -\dfrac{1}{2}

Now substitute into y = x^2:

y = \left(-\dfrac{1}{2}\right)^2 = \dfrac{1}{4}

Check: \sqrt{y} = \dfrac{1}{2}, and x + 1 = \dfrac{1}{2} — it works!

Final Answer: \left(-\dfrac{1}{2}, \dfrac{1}{4}\right) is the only solution.

This problem shows why checking cases with absolute value is important—squaring both sides too early could lead to a wrong or extra solution.

Connecting Algebra to Graphs: Visual Reasoning

On timed tests, stop and picture the shapes. For example, a line and a parabola generally meet twice unless the line is tangent (one point) or misses the curve (no point). Therefore, before crunching numbers, glance at slopes and curvature. This mental preview flags how many answers to expect, guiding elimination in multiple-choice formats.

Common SAT® Traps & Timing Tips

• Sign errors: distributing negative signs incorrectly sinks many students.
• Square-root slips: remember both positive and negative roots when solving x^{2} = k.
• Calculator misuse: typing one parenthesis wrong clouds everything; confirm syntax.

Timing plan:

1. Choose substitution or elimination within 10 seconds.
2. Solve: work carefully but briskly.
3. Check: verify in the original equations to spot extraneous answers.

If algebra looks messy and multiple-choice options differ widely, consider substituting choice values directly. This is often faster than grinding symbolic work.

Quick Reference Vocabulary Chart

Term	Meaning / Key Feature
System of Equations	Two or more equations sharing variables
Solution Set	All ordered pairs that satisfy every equation
Linear Equation	Graph is a straight line; first-degree
Quadratic Equation	Contains x^{2}; graph is a parabola
Substitution	Replace one variable with its expression
Elimination	Add/subtract equations to remove a variable
Intersection	Graphical meeting point(s) of curves
Extraneous Solution	Algebraic result that fails the original equation
Absolute Value	Distance from zero, always non-negative
Radical Equation	Variable appears under a root sign
Rational Equation	Variable in the denominator
Tangent Line	Touches a curve at exactly one point

Two Mixed Practice Questions

Question 1 (Linear–Quadratic)

\begin{cases} y = 3x - 2 \ x^{2} + y^{2} = 10 \end{cases}

What are the solutions?

Solutions:

\left(\dfrac{3 + 2\sqrt{6}}{5},\dfrac{9 + 6\sqrt{6}}{5} - 2\right) and \left(\dfrac{3 - 2\sqrt{6}}{5},\dfrac{9 - 6\sqrt{6}}{5} - 2\right).

(Exact values are accepted on SAT®, but decimals are acceptable if required.)

Question 2 (Absolute Value System)

\begin{cases} |x + y| = 4 \\ y = 2x + 1 \end{cases}

Solve the system.

Solutions: (1,3) and \left(-\dfrac{5}{3},-\dfrac{7}{3}\right).

Final Takeaways & Next Steps

Systems questions test both algebraic fluency and graph sense. Substitution excels when one variable is isolated easily; elimination shines with matching coefficients; graphing or quick slopes help estimate solution counts. Practice under timed conditions, always checking for extraneous roots. Next, strengthen your skills with inequalities and function transformations, building on the same logical foundation used here.

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.