Introduction

Area and perimeter questions often appear in the “Heart of Algebra & Geometry” section of the SAT®. Because the formulas rarely change, these items become easy points once the basics are clear. Therefore, this guide breaks each shape into bite-sized ideas, shows step-by-step examples, and ends with tips on scaling figures. As a result, students gain a dependable plan for every area or perimeter problem on test day.

Geometry Basics Refresher

a. What is Perimeter?

Perimeter is the total length around a 2D figure. Picture a fence surrounding a garden; the wood or wire equals the perimeter.

b. What is Area?

Area counts the amount of flat space inside the figure. Imagine laying carpet; the material covering the floor equals the area.

Fence = perimeter. Carpet = area. Remembering this simple analogy helps separate the two concepts quickly.

Quick-Pick Formula Sheet

Shape	Perimeter / Circumference	Area
Rectangle or Square	P = 2l + 2w	A = lw
Triangle	Add all three sides	A = \dfrac{1}{2}bh
Circle	C = 2\pi r	A = \pi r^{2}
Parallelogram	P = 2(a + b)	A = bh
Trapezoid	Add all four sides	A = \dfrac{1}{2}(b_{1} + b_{2})h

Mini-tip: On the SAT®, shapes are often rotated or drawn inside coordinate grids. However, side markings (tick marks) or right-angle squares still reveal the correct shape quickly.

Core Concept – Rectangles & Squares

Rectangles have opposite sides equal and every angle right. Squares are special rectangles with all sides equal.

Example 1

A classroom whiteboard is 6 ft long and 4 ft tall.

1. Find the perimeter.
2. Find the area.

Solution

To find the perimeter, use the formula for the perimeter of a rectangle:

P = 2l + 2w = 2(6) + 2(4) = 12 + 8 = 20\text{ ft}.

To find the area, use the formula for the area of a rectangle:

A = lw = 6 \times 4 = 24\text{ ft}^2.

So, the perimeter is 20 feet and the area is 24 square feet.

Practice 1: A square sign has a perimeter of 32 in. Find its area. (Answer at the end of the post)

Core Concept – Triangles

SAT® favors three triangle types.

• Right: one 90^\circ angle; this triangle often hides inside rectangles.
• Equilateral: all sides equal; all angles 60^\circ.
• Isosceles: two equal sides; base angles equal.

Area always relies on a true base and its matching height.

Example 2

A triangular road sign has a base length of 10 cm and a height of 12 cm. Find the area.

Solution

To find the area, use the formula for the area of a triangle:

A = \dfrac{1}{2}bh = \dfrac{1}{2}(10)(12) = 5 \times 12 = 60\text{ cm}^2.

So, the area of the sign is 60 square centimeters.

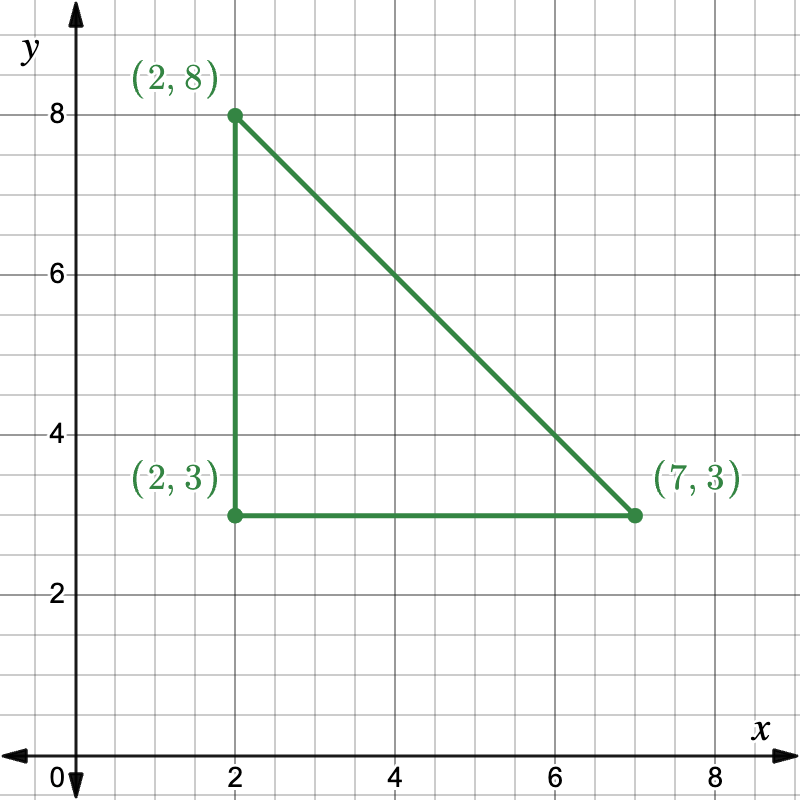
SAT® Alert: In coordinate geometry, the legs of a right triangle often lie on the x– and y-axes, making the reading of base and height directly from coordinates.

Practice 2: Coordinates (2, 3), (2, 8), and (7, 3) form a right triangle. Determine its area. (Answer at the end of the post)

Core Concept – Circles

Key Parts

• Radius r – distance from center to edge
• Diameter d = 2r – edge through center to opposite edge
• Circumference – the circle’s perimeter

Many SAT® items allow \pi to remain in answers; otherwise, approximate \pi \approx 3.14.

Example 3

A semicircular garden bed has a radius of 3 m.

1. Find the perimeter
2. Find the area.

Solution

To find the perimeter, first calculate half the circumference:

\dfrac{1}{2}(2\pi r) = \pi r = \pi(3) = 3\pi.

Then add the straight edge, which is the diameter: 2r = 6.

So, the perimeter is 3\pi + 6 meters.

To find the area, calculate half the area of a full circle:

\dfrac{1}{2}\pi r^2 = \dfrac{1}{2}\pi(3)^2 = \dfrac{1}{2}\pi(9) = 4.5\pi square meters.

So, the perimeter is 3\pi + 6\text{ m} and the area is 4.5\pi\text{ m}^2.

Practice 3: A circular window has a diameter of 20 in. Compute its area in terms of \pi. (Answer at the end of the post)

Core Concept – Special Quadrilaterals (Parallelograms & Trapezoids)

Parallelogram: Opposite sides are parallel; height is the perpendicular distance, not a slanted side.

Trapezoid: Only one pair of parallel sides, called bases b_{1} and b_{2}.

Example 4

A trapezoidal driveway has base lengths of 10 m and 16 m with a height of 5 m. Find the paving area.

Solution

To find the paving area, use the formula for the area of a trapezoid:

A = \dfrac{1}{2}(b_1 + b_2)h = \dfrac{1}{2}(10 + 16)(5) = \dfrac{1}{2}(26)(5) = 13 \times 5 = 65\text{ m}^2.

So, the area to be paved is 65 square meters.

Practice 4: A parallelogram shows a base length of 9 cm and slanted side length of 7 cm. If the height is 4 cm, find its area and perimeter. (Answer at the end of the post)

Scaling and Similar Figures

When every length multiplies by k, important effects follow:

• Lengths → multiply by k
• Areas → multiply by k^{2}
• Volumes → multiply by k^{3} (for 3D)

Mini-Example 5

A photo 4 in by 6 in is enlarged so each side doubles. What is the new area?

Solution

The original area is 4 \times 6 = 24\text{ in}^2.

The scale factor is k = 2, so the area increases by a factor of k^2 = 4.

Multiplying: 24 \times 4 = 96\text{ in}^2.

The new area of the enlarged photo is 96 square inches.

Mixed Practice: Real-World Combo Problem

A backyard plot combines a 20 ft by 10 ft rectangle with a semicircle attached to the 10 ft side. Compute perimeter and total area.

Solution

Drawing a diagram is helpful here. It makes it easier to visualize which parts of the figure contribute to the perimeter and which form the total area. It also helps you recognize that the curved part of the semicircle replaces one of the rectangle’s shorter sides in the perimeter calculation.

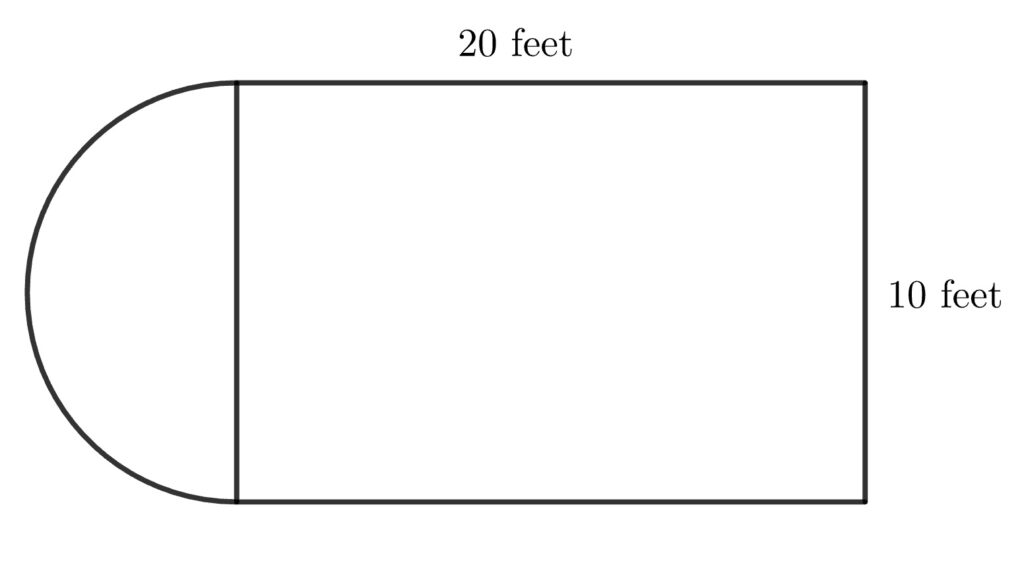
Since the semicircle is attached to the 10 ft side, its radius is 5 ft (half of 10 ft).

Area:

• Rectangle area: 20 \times 10 = 200\text{ ft}^2
• Semicircle area: \dfrac{1}{2}\pi(5)^2 = \dfrac{1}{2}\pi(25) = 12.5\pi\text{ ft}^2
• Total area: 200 + 12.5\pi\text{ ft}^2

Perimeter:

• Three rectangle sides: 20 + 20 + 10 = 50\text{ ft}
• Curved edge of the semicircle: \pi r = 5\pi\text{ ft}
• Total perimeter: 50 + 5\pi\text{ ft}

SAT® Strategy Corner

• Eliminate answer choices with impossible units or negative values.
• Keep fractions until the last step to avoid rounding errors; however, estimate \pi \approx 3.14 only when choices show decimals.
• For grid-in items, leave \pi if the directions accept symbolic answers.
• Drawing an image can help you with the solution.

Common Pitfalls & How to Avoid Them

• Forgetting units: Always label square units for area.
• Mixing radius and diameter: Carefully check which measure is given.
• Wrong triangle height: Height must be perpendicular to the chosen base. Therefore, draw a quick altitude if needed.

Quick Reference Vocabulary Chart

Term	Definition	SAT® Tip
Perimeter	Sum of all side lengths of a 2D figure	Think “fence length”
Area	Amount of surface inside a 2D figure	Think “carpet space”
Radius	Distance from the circle center to the edge	Half of diameter; watch diagrams
Diameter	Distance across the circle through the center	Twice radius; often given directly
Base	Chosen side of a triangle or trapezoid used for height	Pick the side with an easy perpendicular height
Height (Altitude)	Line segment perpendicular to base from opposite vertex or side	Must be a right angle
Scale Factor (k)	Number that multiplies every length in similar figures	Areas change by k^{2}

Solutions to Practice Questions

1. 64 square inches
2. 12.5 square units
3. 100\pi square inches
4. 32 cm

Final Takeaways & Next Steps

Mastering area and perimeter of 2D figures guarantees quick wins on SAT® Math. Remember core formulas, identify shapes fast, and apply the scaling rule. Next, complete timed drills mixing rectangles, triangles, circles, and composite figures. For deeper practice, explore additional geometry sets and strive for automatic recall of every formula in this guide.

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.