Introduction

Triangles seem to pop up on almost every SAT® Math section. In fact, over one-quarter of released questions involve them. That is no accident. When two triangles line up, their matching (corresponding) parts unlock a chain of powerful results: congruence and similarity of triangles​, then the right-triangle trigonometry that follows. Therefore, mastering one idea quickly pays off. This guide breaks the topic down into small, clear steps, allowing you to progress from basic facts to more advanced SAT® strategies with confidence.

Essential Vocabulary Snapshot

• Congruent
• Similar
• Corresponding sides/angles
• Scale factor
• Right triangle, hypotenuse, leg
• Trigonometric ratio

Triangle Congruence Basics

What “congruent” really means

Two figures are congruent when every side length and every angle measure match exactly. Sliding, rotating, or flipping one onto the other will create a perfect overlap.

The Five Congruence Shortcuts

The SAT® rarely asks for formal proofs; however, knowing the “shortcuts” quickly rules out wrong answers.

• SSS (Side-Side-Side)
• SAS (Side-Angle-Side)
• ASA (Angle-Side-Angle)
• AAS (Angle-Angle-Side)
• HL (Hypotenuse-Leg for right triangles)

Example 1

Two triangles, \triangle ABC and \triangle EFC share a vertex C such that {AC} = 5, {BC} = 7, {CE} = 5, {FE} = 7, and m\angle ACB = m\angle E. Prove the triangles are congruent.

Solution

Drawing a diagram is especially helpful in this case because it allows you to clearly see how the sides and angles are arranged. It makes it easier to identify the included angle and how the corresponding parts align, which supports choosing the correct congruence criterion.

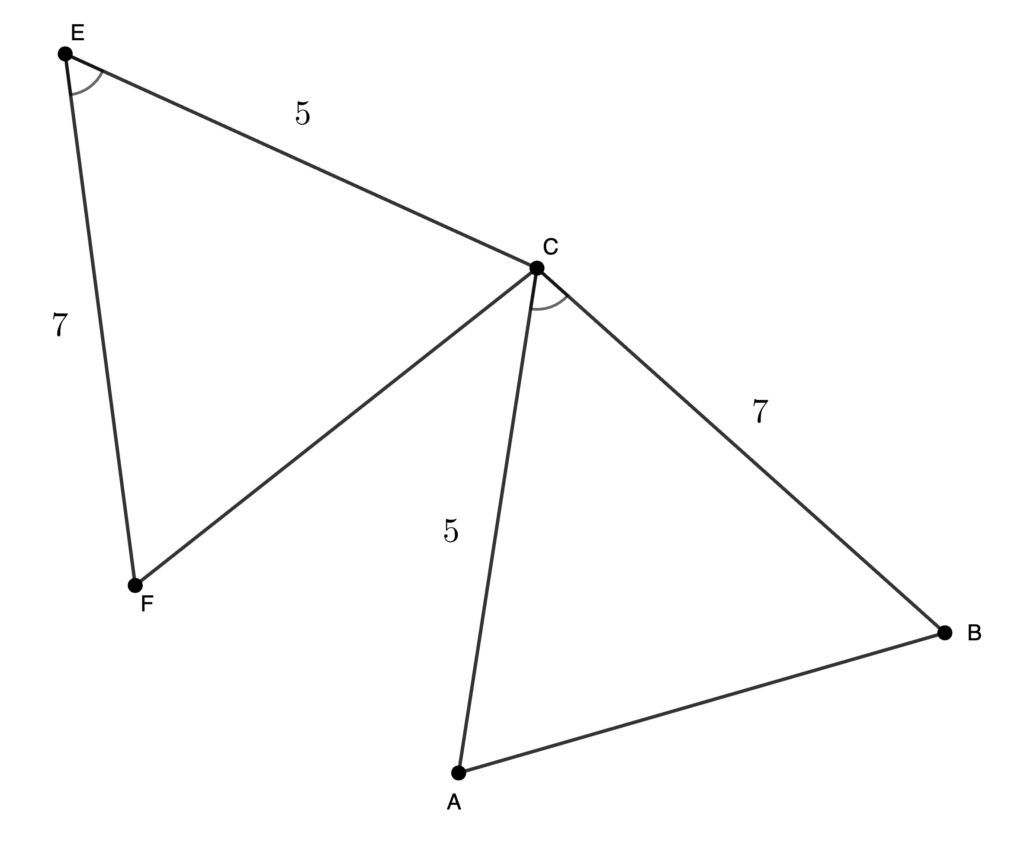
Both triangles have two sides of equal length, with the included angle also equal. This satisfies the Side-Angle-Side (SAS) congruence criterion.

Therefore, \triangle ABC \cong \triangle CFE.

Once congruence is established, corresponding parts can be matched. For example, \overline{AB} = \overline{CF}.

Why it matters

Once congruence is established, any missing length or angle transfers instantly. On a multiple-choice item, that single leap often removes three out of four options.

Triangle Similarity Fundamentals

Definition of similarity

Two figures are similar if they have the same shape but possibly different sizes. As a result, all corresponding angles are equal, and all corresponding sides are in the same ratio.

Three Similarity Criteria

• AA~ (Angle-Angle)
• SAS~ (Side-Angle-Side in proportion)
• SSS~ (three proportional sides)

Proportions and the Scale Factor k

If \triangle PQR \sim \triangle XYZ with scale factor k, then:

\dfrac{PQ}{XY} = \dfrac{QR}{YZ} = \dfrac{PR}{XZ} = k

Example 2

In \triangle ABC, D lies on \overline{AC} and E lies on \overline{AB} so that \overline{DE}\parallel\overline{BC}. Given AD = 3, DC = 6, and AB = 12, find AE.

Solution

Drawing a diagram helps make the relationship between the smaller triangle \triangle ADE and the larger triangle \triangle ABC clearer. The parallel lines create equal corresponding angles, so \triangle ADE \sim \triangle ACB by the AA (Angle-Angle) similarity criterion.

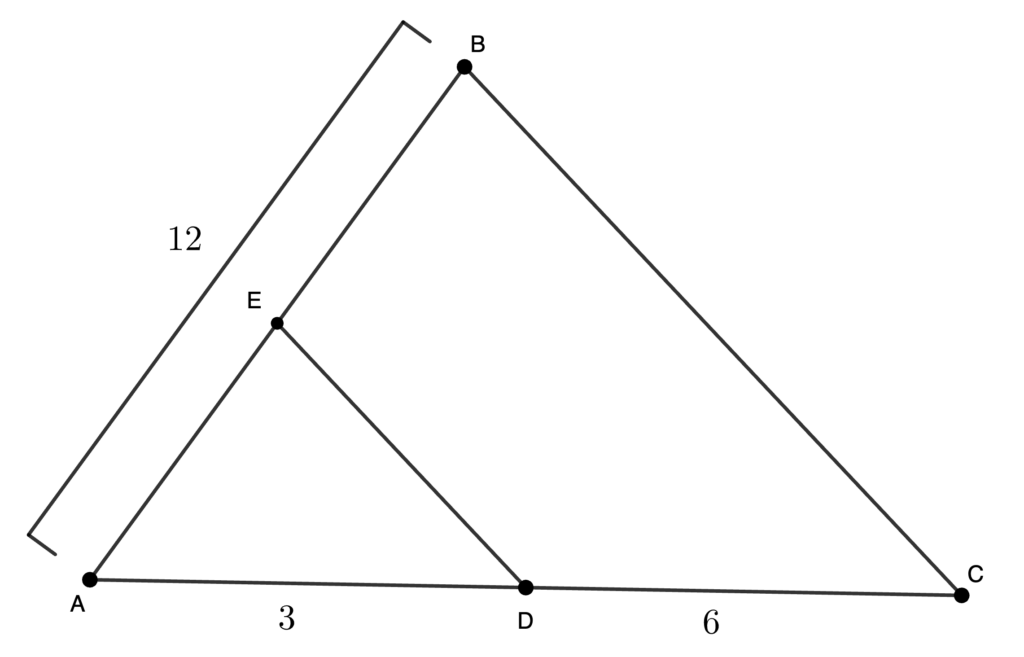
The scale factor between the smaller and larger triangle is:

k = \dfrac{AD}{AC} = \dfrac{3}{3 + 6} = \dfrac{3}{9} = \dfrac{1}{3}

Since AB = 12, and \overline{AE} corresponds to \overline{AB}, we find:

AE = \dfrac{1}{3} \times 12 = 4

So, AE = 4.

Scale Factors in Action

• Multiply every length by k; areas multiply by k^2; volumes (for 3D extensions) multiply by k^3.
• Angles never change.
• Watch for SAT® traps where one length is scaled while an angle remains identical.

Lightning Round

1. A triangle with perimeter 15 is enlarged by k=2. New perimeter? 30.
2. Its area was 18. New area? 18 \times 2^2 = 72.
3. Its angles? Exactly the same measures.

Angle Relationships with Parallel Lines

When a transversal cuts two lines, several angle pairs emerge. The measures of:

• vertical angles are always equal,
• corresponding angles are equal when lines are parallel,
• alternate interior/exterior angles are equal when lines are parallel, and
• same-side interior angles sum to 180^\circ.

Mini Example

Line m is parallel to line n. A transversal forms m\angle 1 = 65^\circ. Find the measure of the alternate interior angle.

Because lines are parallel, the matching alternate interior angle also measures 65^\circ. That angle may later serve as a basis for an argument of AA similarity.

From Similarity to Trigonometry

Similarity in Disguise

Right-triangle trigonometry is simply the study of similar right triangles that share an acute angle. Therefore, the ratios of corresponding sides remain constant and are given special names.

Defining the Big Three Ratios

For an acute angle \theta in a right triangle:

Trigonometric Ratio	Definition
\sin\theta	\dfrac{\text{opposite}}{\text{hypotenuse}}
\cos\theta	\dfrac{\text{adjacent}}{\text{hypotenuse}}
\tan\theta	\dfrac{\text{opposite}}{\text{adjacent}}

Special Right Triangles

• 45-45-90: sides are in the ratio 1:1:\sqrt2.
• 30-60-90: sides are in the ratio 1:\sqrt3:2.

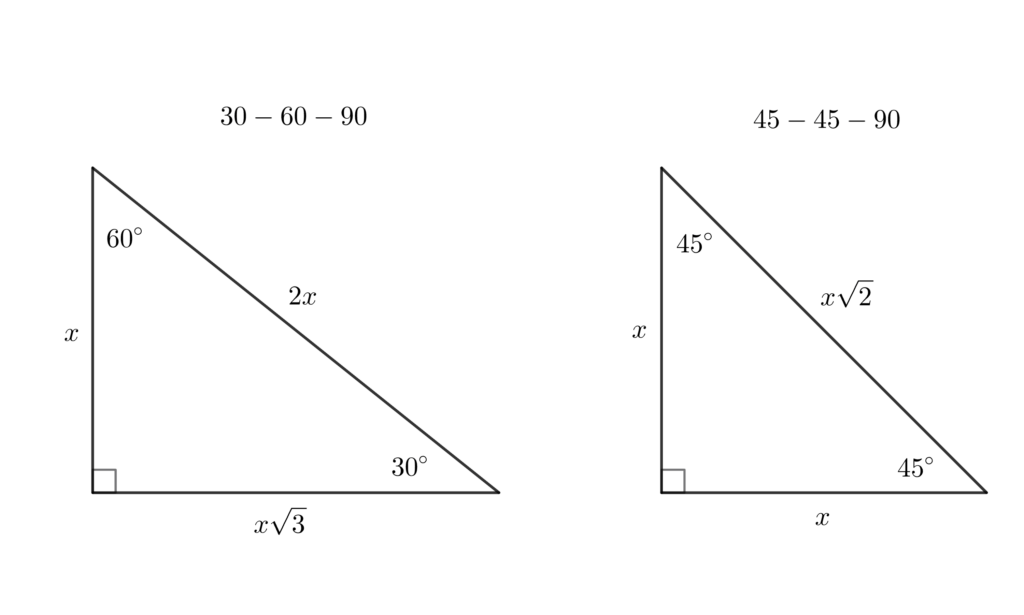
Memorizing these saves time because the SAT® loves exact-value answers.

Example 3

A surveyor stands 80 ft from a tree. The angle of elevation to the top is 32^\circ. Estimate the tree’s height.

Solution

To estimate the tree’s height, draw a right triangle with the adjacent side to the angle as 80 feet and the opposite side as the unknown height h.

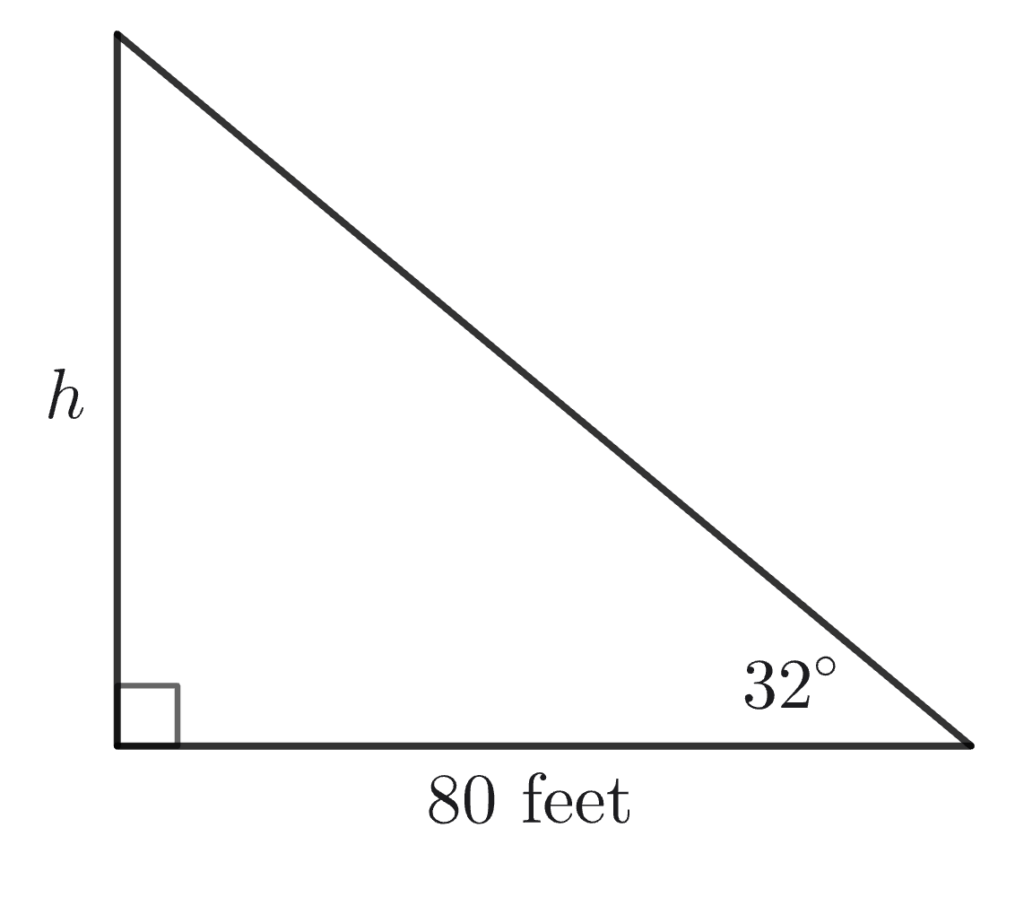
Using the tangent function:

\tan(32^\circ) = \dfrac{h}{80}

Solve for h:

h = 80 \times \tan(32^\circ) \approx 80 \times 0.624 = 49.9\text{ ft}

The tree is about 50 feet tall. Drawing the triangle helps visualize the situation and reminds us that this trigonometric step is just like the proportional reasoning used in triangle similarity.

Strategy Section: Common SAT® Traps & Time-Savers

• “Not drawn to scale” means never trust lengths on sight. Verify with congruence or similarity rules.
• Look for hidden similar triangles, such as an altitude dropped to the hypotenuse or angle bisectors inside an isosceles triangle. These often reveal a quick proportion.
• When an angle is given inside a right triangle, a trig ratio beats writing three separate proportions. Conversely, if a pair of parallel lines is labeled, a similarity shortcut is usually faster than sine or cosine.

Quick Reference Chart

Term	Student-Friendly Definition	SAT® Tip / Memory Aid
Congruent	Same size and same shape	Think “clone”
Similar	Same shape; sides scaled by k	“Mini-me” triangles
SSS, SAS, ASA, AAS, HL	Five tests proving congruence	Check letters: side or angle?
AA, SAS~, SSS~	Tests proving similarity	Two angles are enough
Scale factor k	Multiplier for all lengths	Area grows by k^2
Hypotenuse	Longest side of a right triangle	Across from the right angle
Trig ratios	sin, cos, tan	SOH-CAH-TOA

Practice Questions with Solutions

1. In \triangle XYZ, {XY}=8, {YZ}=6, {ZX}=10. A second triangle has sides 12, 9, 15. Are the triangles congruent, similar, or neither?
2. A right triangle has legs 5 cm and 7 cm. Find the hypotenuse length to the nearest tenth.
3. A 30-60-90 triangle has a hypotenuse length of 14. Find the length of the shorter leg.
4. Parallel lines cut by a transversal form an angle of 110^\circ. What is the measure of the corresponding angle?

Solutions

1. The triangles are similar by SSS.
2. \sqrt{74} \approx 8.6\text{ cm}\
3. 7
4. 110^\circ

Key Takeaways & Next Steps

Triangles dominate SAT® geometry because congruence, similarity, and right-triangle trig all trace back to matching parts. First, confirm whether triangles are equal (congruent) or merely scaled (similar). Then, apply proportions or trig ratios as needed. Timed practice with official SAT® sets will reinforce these moves. For more focused drills, explore additional geometry practice to lock in the speed demanded on test day.

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.