Right triangles appear on almost every SAT® Math section. Therefore, knowing their properties saves time and boosts accuracy. This guide walks through the Pythagorean Theorem, special right-triangle shortcuts, and right-triangle trigonometry. Additionally, worked examples and practice problems reinforce the skill. A quick-reference chart near the end keeps key vocabulary at your fingertips.

Introduction

Although the SAT® often feels unpredictable, one fact remains constant: right-triangle questions show up year after year. Since so many geometry and trigonometry items reduce to the Pythagorean Theorem or its shortcuts, mastering these tools pays big dividends.

This guide provides:

• Plain-language explanations
• Eight fully solved examples
• Matching practice problems
• A vocabulary chart for last-minute review

Keep the steps in mind, and SAT® Math right-triangle questions will soon feel routine.

Pythagorean Theorem Essentials

Statement in Plain Language

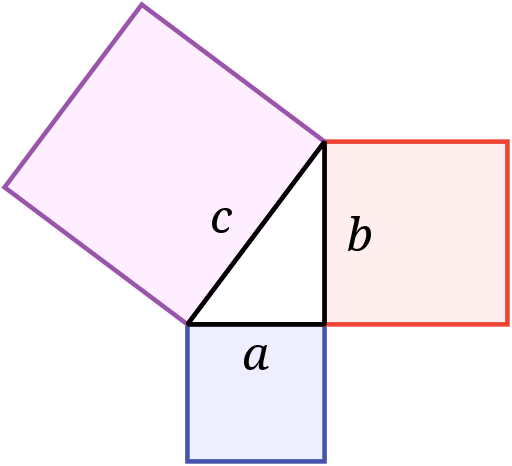
In any right triangle, the square of the hypotenuse (the longest side) equals the sum of the squares of the two legs.

a^{2}+b^{2}=c^{2}

Here, c is the hypotenuse, and a and b are the legs.

When It Works

The theorem applies only to right triangles (one 90^\circ angle). Therefore, always confirm the right angle symbol or wording, such as “forms a right angle.”

Typical SAT® Question Styles

• Find a missing side length.
• Decide whether three numbers can form a right triangle.
• Embed the theorem inside a word problem (e.g., diagonal of a rectangle).

Example 1: Basic Leg Calculation

If a right triangle has a hypotenuse of 13 and one leg of 5, find the length of the other leg.

Solution

1. Identify parts:
   • c = 13, a = 5, b = ?
2. Substitute into the theorem:
   • 5^{2}+b^{2}=13^{2}
3. Simplify squares:
   • 25+b^{2}=169
4. Isolate b^{2}:
   • b^{2}=169-25=144
5. Take the square root:
   • b=\sqrt{144}=12

Practice Problem

What is the length of the hypotenuse if a right triangle’s legs measure 7 and 24.

Solution

7^{2}+24^{2}=c^{2}

49+576=625

c=\sqrt{625}=25

Example 2: Finding the Hypotenuse with Radicals

Find the hypotenuse of a right triangle with legs 6\sqrt{2} and 6.

Solution

1. Substitute values:
   • \left(6\sqrt{2}\right)^2+6^{2}=c^{2}
2. Square each term carefully:
   • 72+36=c^{2}
3. Add:
   • 108=c^{2}
4. Simplify the radical:
   • c=\sqrt{108}=\sqrt{36\cdot3}=6\sqrt{3}

Practice Problem

A rectangle is 5 cm by 8 cm. What is the length of its diagonal in simplest radical form?

Solution

The diagonal forms the hypotenuse:

5^{2}+8^{2}=d^{2}

25+64=89

d=\sqrt{89}

Pro Tips

• Estimate first. If legs are about 10, expect a hypotenuse just over 14 (because 10\sqrt{2}\approx14.1).
• Make sure to always reduce radicals for final answers.
• Beware of “almost” right triangles; the SAT® sometimes lists near-miss numbers like 6-8-11.

Special Right-Triangle Shortcuts

The 45-45-90 Pattern

If a right triangle is isosceles (two equal legs), its side lengths always fit x,x,x\sqrt{2}.

The 30-60-90 Pattern

If a right triangle has angles 30^\circ, 60^\circ, and 90^\circ, it has sides x (short), x\sqrt{3} (long leg), and 2x (hypotenuse).

When to Use a Shortcut

Use the pattern when the angle measures are 30^\circ, 45^\circ, 60^\circ, or when the legs are equal. Otherwise, fall back on the Pythagorean Theorem.

Example 3: 45-45-90 Perimeter Problem

What is the perimeter of a 45-45-90 triangle if the length of one leg is 9. Find its perimeter.

1. Hypotenuse:
   • 9\sqrt{2}
2. Perimeter:
   • 9+9+9\sqrt{2}=18+9\sqrt{2}

Practice Problem

A 45-45-90 triangle has a hypotenuse of 12\sqrt{2}. What is one leg?

Solution

Divide by \sqrt{2}:

12\sqrt{2}\div\sqrt{2}=12.

Example 4: 30-60-90 Word Problem

If a 12-foot ladder rests against a wall, forming a 30^\circ angle with the ground, how high up the wall does the ladder reach?

Solution

The hypotenuse of the triangle is 12 ft, and the angle opposite the wall is 30^\circ. In a 30^\circ-60^\circ-90^\circ triangle, the side opposite the 30^\circ angle is the short leg, and the hypotenuse is always twice the length of the short leg.

Let the short leg be x. Then, 2x = 12 \Rightarrow x = 6.

So, the height on the wall (the short leg) is 6 ft

Practice Problem

Here, the hypotenuse is a side of the equilateral triangle: 10 units. So, 2x = 10 \Rightarrow x = 5.

Now use the pattern to find the height:

\text{height} = x\sqrt{3} = 5\sqrt{3}

Therefore, the height of the triangle is 5\sqrt{3} units, or approximately 8.7 units.

Solution

Short side = 5; height = 5\sqrt{3}.

Quick-Glance Comparison

• 45-45-90: multiply or divide by \sqrt{2}.
• 30-60-90: multiply or divide by 2 or \sqrt{3} depending on which side is known.
• Both save time over the general theorem.

Right-Triangle Trigonometry Basics

SOH-CAH-TOA Definitions

For any right triangle with acute angle \theta:

• Sine: \sin\theta=\dfrac{\text{opposite}}{\text{hypotenuse}}

• Cosine: \cos\theta=\dfrac{\text{adjacent}}{\text{hypotenuse}}

• Tangent: \tan\theta=\dfrac{\text{opposite}}{\text{adjacent}}

Using Similarity

Similar right triangles keep the same ratio of sides, so trig functions depend only on angle size, not on triangle size.

Complementary Angle Relationship

Because \theta+\phi=90^\circ,

\sin\theta=\cos(90^\circ-\theta) and vice versa.

Example 5: Finding a Side Using Sine

In a right triangle, \sin 40^\circ=\dfrac{x}{15}, where 15 is the hypotenuse. Find x.

Solution

First, rearrange the equation.

x=15\sin40^\circ

Next, use a calculator (no-calc section would give approximations):

\sin40^\circ\approx0.643; therefore x\approx9.65.

Practice Problem

Given \cos 30^\circ=\dfrac{y}{10} and 10 is the hypotenuse, find y.

Solution

y=10\cos30^\circ=10\cdot\dfrac{\sqrt{3}}{2}=5\sqrt{3}\approx8.66

Example 6: Finding an Angle with Inverse Trig

A right triangle has legs 8 and 15. Find the measure of the angle opposite the 8-unit leg.

Solution

Since we know the leg lengths, we want to use the tangent.

\tan\theta=\dfrac{8}{15}

To calculate the angle, use the inverse tangent.

• \theta=\tan^{-1}\left(\dfrac{8}{15}\right)\approx28.1^\circ

Practice Problem

A ramp rises 2 ft over a horizontal run of 9 ft. What is the ramp’s angle of elevation to the nearest degree?

Solution

\theta=\tan^{-1}\left(\dfrac{2}{9}\right)\approx12.5^\circ\approx13^\circ

Calculator vs. No-Calculator Sections

• On the no-calculator section, the SAT® chooses “nice” angle values (30^\circ, 45^\circ, 60^\circ) or hides the answer in radical form.
• On the calculator section, expect any angle; use the trig keys quickly.

Putting It All Together: Mixed Practice

Blended SAT® Skills

Several SAT® Math questions require a special-triangle shortcut first and trigonometry second, or vice versa. Therefore, practice switching tools smoothly.

Example 7: Combo Question

A right triangle has legs in a 1:2 ratio, and the smaller leg equals 7.

Solution

a) Legs: 7 and 14.

Hypotenuse:

7^{2}+14^{2}=c^{2}

49+196=245

c=\sqrt{245}=7\sqrt{5}

b) Angle:

\sin\theta=\dfrac{7}{7\sqrt{5}}=\dfrac{1}{\sqrt{5}}\approx0.447

\theta\approx26.6^\circ

Answers: 7\sqrt{5} and approximately 27^\circ.

Practice Problem

A rectangle is 6 m by 8 m. If a wire runs from one corner to the midpoint of the opposite side, find the wire’s length.

Solution

1. Diagonal corner-to-corner = 10 (6-8-10 triangle).
2. Midpoint cuts the diagonal in half:
   • Wire = 10\div2=5 m.

Example 8: Geometry Word Problem with Special-Right Shortcut

An isosceles right triangle has an area of 32 cm². Find the length of its hypotenuse.

Solution

1. For a 45-45-90 triangle, let each leg be x.
2. Area: \frac{1}{2}x^{2}=32 → x^{2}=64 → x=8.
3. Hypotenuse: x\sqrt{2}=8\sqrt{2}.

Practice Problem

A 30-60-90 triangle has a long leg of 9\sqrt{3}. What is its perimeter?

Solution

Long leg = x\sqrt{3}=9\sqrt{3} → x=9.

Hypotenuse = 2x=18.

Perimeter = 9+9\sqrt{3}+18=27+9\sqrt{3}.

Answer: 27+9\sqrt{3}.

Common Missteps

• Mixing up which side is “opposite” vs. “adjacent.”
• Forgetting to double or halve in special triangles.
• Rounding too soon; keep at least three decimal places until the final answer.

Speed Strategies for Test Day

• Spot clue words: right triangle, altitude, 45^\circ, equilateral height.
• Choose the fastest tool: If angles are 30^\circ or 60^\circ, jump to the 30-60-90 pattern. If only sides appear, use the Pythagorean Theorem.
• Estimate: Before calculating, guess which answer choice seems reasonable.
• Calculator tactics: Store intermediate values (STO > ALPHA) to avoid re-typing.

Quick Reference Vocabulary Chart

Term	Definition	SAT® Tip
Pythagorean Theorem	a^2 + b^2 = c^2 for right triangles	Confirm the right angle before using
Hypotenuse	Longest side opposite 90^\circ	Always “c” in the formula
Leg	One of the two shorter sides	Labeled “a” or “b”
45-45-90 Triangle	Isosceles right triangle; sides x, x, x√2	Multiply leg by \sqrt{2} for hypotenuse
30-60-90 Triangle	Short side x, long leg x√3, hypotenuse 2x	Short side sits opposite 30^\circ
Sine	\dfrac{\text{Opposite}}{\text{Hypotenuse}}	\sin θ = \cos (90^\circ – θ)
Cosine	\dfrac{\text{Adjacent}}{\text{Hypotenuse}}	\cos^\circ θ + \sin^\circ θ = 1
Tangent	\dfrac{\text{Opposite}}{\text{Adjacent}}	\tan θ = \dfrac{\sin θ}{\cos θ}
Complementary Angles	Two angles adding to 90^\circ	Swap sine & cosine

Final Checklist and Next Steps

1. Know the three most common triples, including 3-4-5, 5-12-13, 8-15-17.
2. Memorize 45-45-90 and 30-60-90 patterns cold.
3. Use SOH-CAH-TOA only after labeling opposite, adjacent, and hypotenuse correctly.
4. Reduce radicals and leave π untouched unless asked for a decimal.
5. Time each practice set, as pacing on test day is crucial.

Ready for more SAT® Math practice? Explore additional right-triangle drills and timed quizzes to lock in these skills before test day. Good luck—you now have the tools to conquer every Pythagorean and trigonometry problem the SAT® can throw your way!

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.