Circles show up often on the SAT® Math Test. They may appear alone, mixed with coordinate geometry, or tied to trigonometry. Therefore, solid skills with the equation and graph of a circle​ boost both speed and accuracy. This guide explains the must-know facts—from writing an equation to using radians—all in clear, bite-sized steps.

Why Circles Matter on the SAT®

• Roughly 10\% of SAT® Math questions rely on circle properties.
• Questions blend algebra, geometry, and trigonometry.
• Mastery lets students solve quickly and save time for tougher items.

Key skills covered: equation writing, graph reading, radians, arc length, the unit circle, and more.

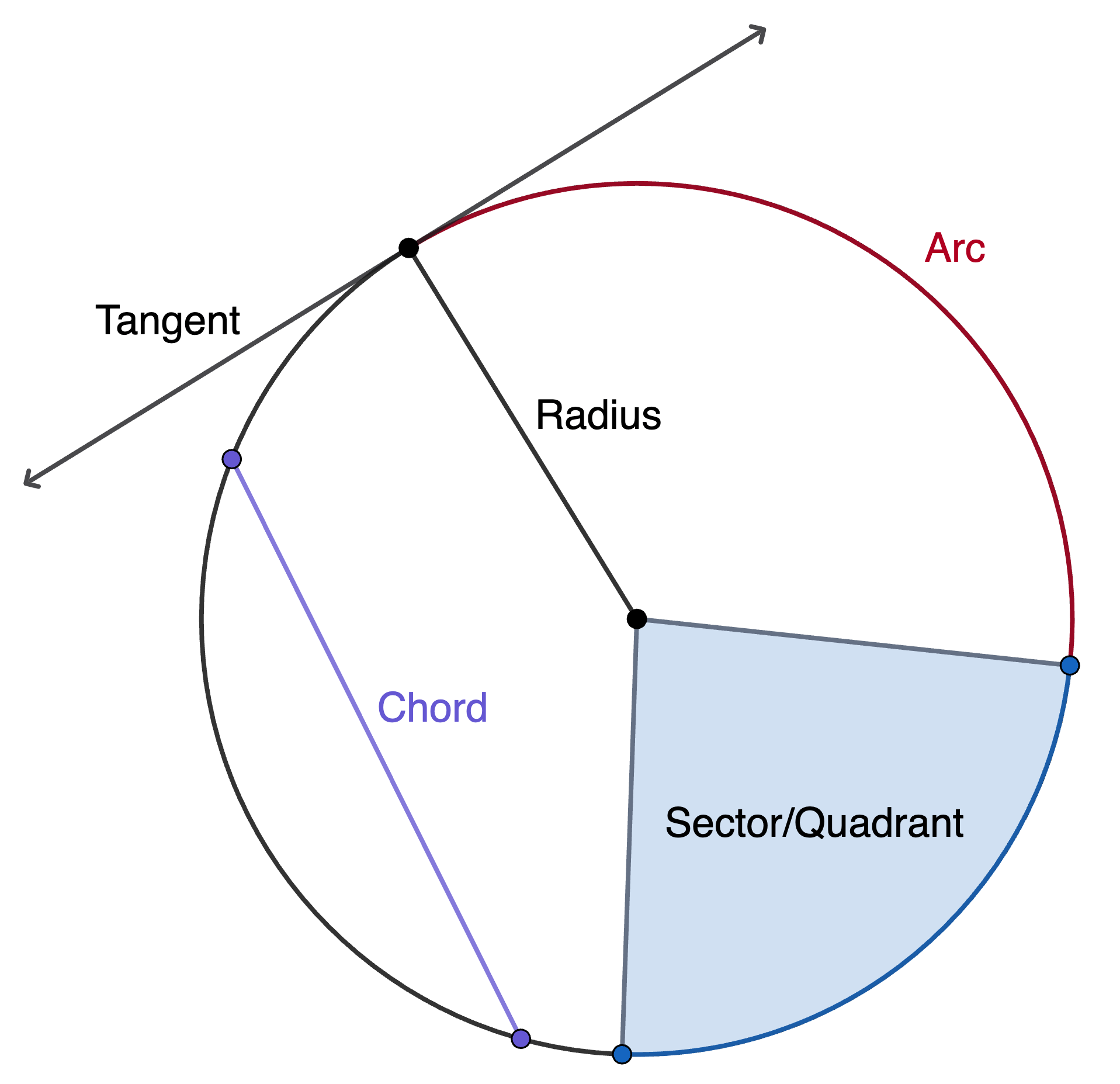
Circle Vocabulary & Key Properties

Essential Parts of a Circle

• Center
• Radius
• Diameter
• Chord
• Tangent
• Secant
• Arc
• Sector

Must-Know Theorems and Facts

• All radii in the same circle are congruent.
• A radius is perpendicular to a tangent at the point of tangency.
• Inscribed angle = \frac{1}{2} (intercepted arc).
• A diameter that bisects a chord is perpendicular to that chord.

Example 1: Identify Parts

A circle has center O. Point T is on the circle. Line OT is extended to meet point P outside the circle. Line TP touches the circle only at T.

1. Name a radius.
2. Name a tangent segment.
3. Which two segments are perpendicular?

Solution

1. \overline{OT} is a radius because it joins the center to the circle.
2. \overline{TP} is a tangent segment because it touches the circle at one point.
3. Radius \overline{OT} is perpendicular to tangent \overline{TP} at T (radius-tangent theorem).

Standard Form of a Circle’s Equation

Deriving the Formula

Using the Distance Formula, any point (x,y) is distance r from center (h,k):

r=\sqrt{(x-h)^2+(y-k)^2}

Squaring both sides gives the standard form:

x-h^2+(y-k)^2=r^2

Reading Key Features Quickly

• Center → (h,k)
• Radius → r (square root of the right-hand number)

Example 2: Write an Equation

Write the equation of a circle with center (3, –2) and radius 5.

Solution

x-3^2+(y+2)^2=5^2

So the equation is x-3^2+(y+2)^2=25.

General Form → Standard Form: Completing the Square

Recognizing the General Form

x^2+y^2+Dx+Ey+F=0

Completing-the-Square Steps

1. Group x and y terms.
2. Move the constant to the other side.
3. Add the square of half the x-coefficient to both sides.
4. Repeat for y.
5. Factor each perfect square trinomial.

Example 3: Convert & Interpret

Convert x^2+y^2-6x+4y-3=0 to standard form and state the center and radius.

Solution

1. Group: (x^2-6x)+(y^2+4y)=3
2. Half of –6 is –3; square is 9. Half of 4 is 2; square is 4. Add these to both sides:
   • (x^2-6x+9)+(y^2+4y+4)=3+9+4
3. Factor: x-3^2+(y+2)^2=16

So, center = (3,-2); radius = \sqrt{16}=4.

Transformations: How Equation Changes Affect the Graph

Horizontal & Vertical Shifts

• Change h: moves circle left/right.
• Change k: moves circle up/down.

Stretching or Shrinking

• Change r: larger r → bigger circle; smaller r → smaller circle.

Example 4: Predict Changes

Original: x-1^2+(y+4)^2=9

1. If r is doubled, radius becomes 6, so equation: x-1^2+(y+4)^2=36.
2. If h decreases by 3, new center = (–2, –4) and equation: (x+2)^2+(y+4)^2=9.

From Graph to Equation

Reading from a Grid

Find the center (intersection of axes of symmetry) and count the radius squares. Make sure you only use a radius that is either vertical or horizontal!

Partial Information Techniques

• If you’re given the endpoints of a diameter, the center is the midpoint.
• With three non-collinear points, use the perpendicular bisector method or system of equations.

Example 5: Diameter Endpoints

A circle passes through A(1, 2) and B(5, 2). The center lies on x = 3.

1. Because A and B share the same y-value, \overline{AB} is horizontal. Its midpoint is (3, 2).
2. The center must be this midpoint (x = 3 line matches). So, the center is (3, 2).
3. The radius is the distance from center to A:
   • r=\sqrt{(3-1)^2+(2-2)^2}=2
4. Equation: x-3^2+(y-2)^2=4.

Radians, Arc Length, & Sector Area

Degrees ↔ Radians

180^\circ=\pi\text{ radians}

To convert: multiply degrees by \dfrac{\pi}{180} or radians by \dfrac{180}{\pi}.

Arc Length

s=r\theta (θ in radians)

Sector Area

A=\tfrac12 r^2\theta

Example 6: Sector Area

Find the area of a 60^\circ sector in a circle of radius 7.

1. Convert 60^\circ: 60^\circ=\dfrac{\pi}{3}\text{ rad}
2. Apply the formula:
   • A=\tfrac12(7)^2\left(\dfrac{\pi}{3}\right)=\tfrac12(49)\left(\dfrac{\pi}{3}\right)=\dfrac{49\pi}{6}

So the area is \dfrac{49\pi}{6} square units.

Trigonometric Ratios & the Unit Circle

Coordinates on the Unit Circle

Any point on the unit circle satisfies x^2+y^2=1. the coordinates are (\cos{x},\sin{x}).

Linking to Sine and Cosine Graphs

As θ increases, the y-coordinate traces the sine wave, while the x-coordinate traces cosine.

Example 7: Evaluate \sin225^\circ

1. 225^\circ = 180^\circ + 45^\circ, placing the angle in Quadrant III.
2. The reference angle is 45^\circ.
3. Sine is negative in Quadrant III, so:
   • \sin225^\circ=-\dfrac{\sqrt2}{2}

Tangents, Chords, & Angle Properties

Tangent-Radius Right Angle

A tangent makes a 90^\circ angle with the radius at the point of contact.

Inscribed Angle Theorem

The measure of an inscribed angle equals half the measure of its intercepted arc.

Example 8: Inscribed Angle

An inscribed angle intercepts a 110^\circ arc. Its measure is:

\dfrac12(110^\circ)=55^\circ

Quick Reference Vocabulary Chart

Term	Definition	SAT® Tip
Radius	Segment from the center to the circle	Often needed for distance or area
Diameter	Twice the radius; passes through the center	Midpoint gives the center quickly
Chord	Segment joining two points on a circle	A diameter is the longest chord
Tangent	Line touching circle at exactly one point	Perpendicular to the radius
Arc Length	Curve distance along a circle	Use s=r\theta with θ in radians
Sector Area	“Pizza slice” region	A=\tfrac12 r^2\theta
Standard Form	x-h^2+(y-k)^2=r^2	Read the center and radius at a glance
General Form	x^2+y^2+Dx+Ey+F=0	Complete the square to graph

Practice Set

Solve without a calculator if possible.

1. Write the equation of a circle with center (–4, 1) and a diameter of 10.
2. Convert x^2+y^2+8x-2y-15=0 to standard form; state center and radius.
3. In a circle of radius 9, find the length of an arc that subtends 2.5 radians.
4. An inscribed angle measures 37^\circ. What is the measure of its intercepted arc?

Solutions

1. (x+4)^2+(y-1)^2=25
2. Center = (–4, 1); radius = \sqrt{32}=4\sqrt2
3. s=r\theta=9(2.5)=22.5 units
4. 74^\circ

Conclusion & Next Steps

This guide covered circle vocabulary, standard and general equations, graph transformations, radians, arc length, sector area, and useful angle properties. Consistent practice—especially under timed conditions—turns these facts into automatic tools on SAT® day. For more targeted drills, explore additional circle problem sets and official SAT® practice tests.

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.