Series convergence is a vital topic in AP® Calculus AB-BC because it lays the groundwork for understanding more advanced ideas in calculus. In particular, absolute vs conditional convergence plays a significant role in analyzing infinite sums. Mastering these concepts makes it easier to tackle higher-level courses and complex summation problems later on. Therefore, it is important to practice identifying series that either converge absolutely or only converge conditionally.
This article will recap the basics of series, highlight the significance of absolute convergence, and explain how conditional convergence differs. It will also offer step-by-step examples, so students can develop greater confidence when applying these methods in exams and real-world problems.
What We Review
Recap: What Is a Series?
Definition of a Series
A series is the sum of infinitely many terms. In notation, a simple series can be written as:
\sum_{n=1}^{\infty} a_nHere, a_n refers to the nth term in the sequence. A series can either converge (settle on a finite value) or diverge (grow without bound or fail to settle).
Common Tests for Convergence (High-Level Recap)
In calculus, several standard tests help determine convergence:
- Comparison Test
- Ratio Test
- Root Test
However, these tests can be combined or compared with additional tools (like the Alternating Series Test) to decide whether a series is absolutely convergent or conditionally convergent.
Absolute Convergence
Definition
A series \sum_{n=1}^{\infty} a_n converges absolutely if the series formed by the absolute value of each term, \sum_{n=1}^{\infty} |a_n|, also converges. In other words, if taking all terms as positive still yields a convergent sum, then the original series is absolutely convergent.
Absolute convergence implies that the original series also converges (without needing to consider signs). Thus, absolute convergence is viewed as a stronger condition because it guarantees stability under any rearrangement of terms.
Importance
Absolute convergence is crucial because:
- It ensures that rearranging series terms does not change the sum.
- It implies stronger consistency in problem-solving, as absolutely convergent series often simplify analyses.
Moreover, many theorems in higher mathematics rely on absolute convergence to guarantee certain properties, such as uniform convergence in advanced settings.
Example Problem (Step-by-Step)
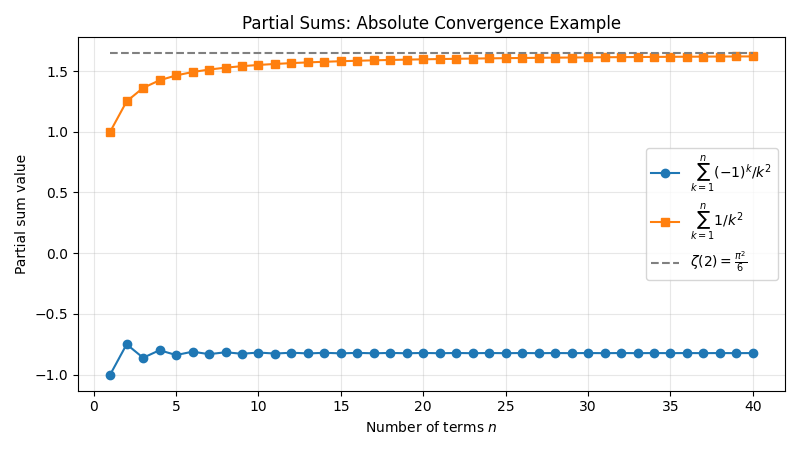
- Consider the series: \sum_{n=1}^{\infty} \frac{(-1)^n}{n^2}
- To check for absolute convergence, take the absolute value of each term: \sum_{n=1}^{\infty} \left|\frac{(-1)^n}{n^2}\right| = \sum_{n=1}^{\infty} \frac{1}{n^2}
- Next, recall that \sum_{n=1}^{\infty} \frac{1}{n^2} is a well-known convergent p-series, since p=2 > 1. Therefore, the absolute value series converges.
- Because the absolute value series converges, the original series \sum_{n=1}^{\infty} \frac{(-1)^n}{n^2} converges absolutely.
- Key takeaway: If a series converges absolutely, it also converges in its standard form. This confirms that no rearrangement changes the sum.
Conditional Convergence
Definition
A series is conditionally convergent if it converges in its original form but does not converge absolutely. In other words, once all terms are turned positive, the series fails to converge. Despite its convergence in the original configuration, the absolute value version diverges.
Implications
Conditionally convergent series can exhibit surprising properties:
- Rearranging the order of terms might change the value of the sum.
- They are more delicate to handle than absolutely convergent series.
The importance of recognizing a conditionally convergent series lies in understanding its limitations and knowing when to apply specialized tests such as the Alternating Series Test.
Example Problem (Step-by-Step)
- Consider the series: \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n} (also known as the alternating harmonic series)
- Decide which convergence test to use. The Alternating Series Test is a good candidate because the terms alternate signs and decrease in magnitude.
- Check convergence:
- The terms \frac{1}{n} decrease toward zero as n increases.
- Therefore, by the Alternating Series Test, \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n} converges.
- However, to test absolute convergence, consider \sum_{n=1}^{\infty} \left| \frac{(-1)^{n+1}}{n} \right| = \sum_{n=1}^{\infty} \frac{1}{n}, which is the harmonic series. This harmonic series diverges.
- Final conclusion: The series converges, but not absolutely. It is conditionally convergent.
Comparing Absolute vs Conditional Convergence
Summary of Key Differences
- Absolute convergence guarantees that the series \sum |a_n| converges, while conditional convergence fails this test.
- In absolute convergence, rearranging terms never changes the sum. However, in conditionally convergent series, rearranging terms can lead to different sums.
- When terms are large and decrease slowly (like 1/n), suspect conditional convergence rather than absolute convergence.
Real-World/Conceptual Cases
These concepts arise often in advanced calculus and analysis:
- Understanding absolute vs conditional convergence helps in checking if integrals and power series converge in certain regions.
- Recognizing a conditionally convergent series helps anticipate potential issues in numerical computations.
Quick Reference Chart: Important Vocabulary and Definitions
| Term | Definition |
| Absolute Convergence | A series \sum a_n is absolutely convergent if \sum |a_n| converges. |
| Conditional Convergence | A series converges but not absolutely, meaning \sum |a_n| diverges. |
| Divergence | A series fails to settle on a finite sum and does not converge. |
| Ratio Test | A method using \lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right| to check convergence. |
| Root Test | A method using \lim_{n\to\infty}\sqrt[n]{a_n} to check convergence. |
| Alternating Series Test | A test checking if terms alternate and decrease in magnitude to zero, ensuring convergence. |
Conclusion
Absolute convergence vs conditional convergence plays a central role in the study of infinite series. Because absolute convergence indicates a stronger form of convergence, it is commonly the first choice to test. If absolute convergence fails, the series may still converge conditionally under certain conditions.
Students are encouraged to practice using tests such as the Ratio Test, Root Test, and Alternating Series Test on different series. Having a solid grasp of these methods not only prepares them for the AP® Calculus AB-BC exams but also paves the way for success in more advanced courses.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








