What We Review
Introduction
The average rate of change formula is a key concept in AP® Calculus AB and BC. It measures how a function’s output changes over a specific interval. This becomes especially important when analyzing motion, growth patterns, or any process that varies over time. Therefore, understanding how to apply the average rate of change formula provides a solid foundation for many higher-level calculus ideas.
However, it is not just about calculating the result. The deeper meaning behind the formula shows how functions behave between two points. This insight then paves the way for the concept of the instantaneous rate of change, which is the backbone of derivatives.
Understanding the Concept of Rate of Change
Rate of change indicates how one quantity shifts in relation to another quantity. In simpler terms, it measures how fast or slow something is changing. For example, speed is a rate of change of distance with respect to time.
However, there is a difference between average rate of change and instantaneous rate of change. The average rate of change looks at the total change over an interval, while the instantaneous rate of change shows how a function changes at a single point. In calculus, the idea of a limit helps describe how a function behaves as it approaches a specific spot.
In fact, limits help transition from average changes, which happen over an interval, to instantaneous changes. Without limits, studying a function’s rate of change at a single point would be impossible, since there would be no interval width to calculate.
Average Rate of Change Formula
The average rate of change formula generally appears as: \frac{f(b) - f(a)}{b - a}
This expression finds how much a function’s output changes between two input values a and b. Therefore, it gives a straightforward way to measure a function’s overall growth or decline over that span.
When interpreting this formula, the denominator (b - a) must be nonzero. If b - a = 0, then the formula is undefined because division by zero has no meaning. Therefore, it is important to choose two different input values. Additionally, the function must be defined at both a and b, so domain restrictions are crucial to consider.
Step-by-Step Example of Average Rate of Change
Consider the function f(x) = x^2. Find the average rate of change from x = 2 to x = 5.
- Identify the function and the interval.
- Function: f(x) = x^2
- Interval endpoints: a = 2 and b = 5
- Calculate the function values at x = 2 and x = 5.
- f(2) = 2^2 = 4
- f(5) = 5^2 = 25
- Plug these into the average rate of change formula.
- Average Rate of Change \frac{f(5) - f(2)}{5 - 2} = \frac{25 - 4}{3}
- Simplify the expression.
- \frac{21}{3} = 7
Therefore, the average rate of change from x = 2 to x = 5 is 7. This result means that on average, the function f(x) = x^2 increases by 7 units for each unit increase in x within the given interval.
Moving from Average to Instantaneous Rate of Change
While the average rate of change formula is useful, it does not reveal what happens at a single point. The instantaneous rate of change, on the other hand, captures how quickly a function changes at a precise moment.
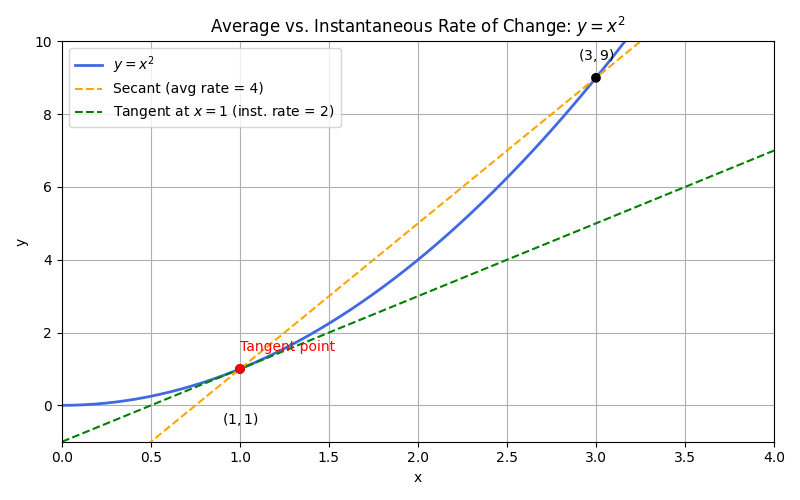
Limits bridge the gap between average and instantaneous rates of change. By bringing the two interval points infinitely close, the average rate of change turns into the instantaneous rate of change. In calculus terms, this limit-based value is the derivative.
Therefore, the limit definition of the derivative is often described as the limit of the average rate of change. This idea is central to all of differential calculus, since it brings out the slope of the curve at exactly one point.
Step-by-Step Example of Instantaneous Rate of Change
Consider again f(x) = x^2. Find the instantaneous rate of change at x = 3 using the limit definition of the derivative.
- Write down the limit definition of the derivative.
- The derivative f'(x) at a point x is given by: f'(x) = \lim\limits_{h \to 0} \frac{f(x + h) - f(x)}{h}
- Substitute the function f(x) = x^2 and the value x = 3.
- f'(3) = \lim\limits_{h \to 0} \frac{(3 + h)^2 - 3^2}{h}
- Expand and simplify inside the numerator.
- (3 + h)^2 = 9 + 6h + h^2
- So: \frac{(3 + h)^2 - 9}{h} = \frac{9 + 6h + h^2 - 9}{h} = \frac{6h + h^2}{h}
- Factor out h.
- \frac{6h + h^2}{h} = 6 + h
- Take the limit as h approaches 0.
- \lim\limits_{h \to 0} (6 + h) = 6
Thus, the instantaneous rate of change (the derivative) of f(x) = x^2 at x = 3 is 6. This value indicates how fast the function is changing right at x = 3.
Quick Reference Chart
| Term | Definition / Key Feature |
| Average Rate of Change | \frac{f(b) - f(a)}{b - a} over an interval [a, b]. |
| Instantaneous Rate of Change | The limit of the average rate of change as b approaches a. Often called the derivative at a point. |
| Limit | A value that a function or sequence approaches as the input gets closer to a specific point. |
| Independent Variable | The input variable of a function, often denoted by x. |
| Domain | The set of all input values for which a function is defined. |
Conclusion
The average rate of change formula is a cornerstone in AP® Calculus because it lays the groundwork for the concept of the derivative. It measures how much a function rises or falls between two points. However, to see what happens at just one point, the instantaneous rate of change becomes necessary. This second concept relies on limits and forms the crucial link to differentiation.
Studying both average and instantaneous rates of change will build the calculus knowledge needed for more advanced topics. Therefore, practicing these calculations and understanding their meaning will serve as an essential part of preparing for deeper explorations in AP® Calculus AB and BC.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








