Computers use a special language behind the scenes, and it all starts with binary numbers. These numbers are the foundation of how devices store, process, and display information. Therefore, understanding how binary numbers work provides insight into data abstraction and how bits fit together to represent everything from website content to mobile apps. Bits are grouped into bytes, characters, colors, or even entire images. As a result, binary numbers form the basis for digital data in modern technology.
Studying binary numbers helps in learning how to read binary numbers, how to convert binary numbers in decimal, and how to convert decimals in binary numbers. By mastering these concepts, it becomes easier to see how computers interpret seemingly simple zeros and ones into complex, useful information. Next, explore each concept step-by-step to unravel the power of binary.
What We Review
What Are Binary Numbers?
Binary numbers are numbers written using only two symbols: 0 and 1. This system is called base 2. In contrast, the numbers used every day (0 through 9) belong to the decimal system, or base 10.
- In base 10, each digit can be any value from 0 to 9.
- In base 2, each digit (bit) can only be 0 or 1.
Think of it like a light switch that’s either on (1) or off (0). Despite having just two choices per digit, binary numbers can represent enormous amounts of data. Computers use these simple digits to store documents, videos, music, and games. Therefore, understanding binary numbers is the key to seeing how data abstraction works in computing.
Example (Decimal vs. Binary):
- Decimal 5 → Binary 101
- Decimal 6 → Binary 110
Understanding Bits and Bytes
A bit is the smallest unit of digital information and can be either 0 or 1. The term bit comes from “binary digit.” Next, a byte is a group of eight bits. This grouping is critical because many systems handle data in byte-sized chunks.
For instance, imagine you have eight switches in a row. Each switch can be on or off, giving a total of 2⁸ (256) possible combinations. As a result, a single byte (eight bits) can hold 256 distinct patterns. These patterns might represent letters, numbers, or colors, depending on the context.
Visualizing bits:
- 00000000 might represent the number 0.
- 11111111 might represent the maximum value for one byte.
However, the meaning of those bits can change if the program interprets them differently, which illustrates another layer of data abstraction.
Reading Binary Numbers
Reading binary numbers follows a similar principle to reading decimal numbers, except each position represents a power of 2 instead of a power of 10. Therefore, the rightmost digit corresponds to 2⁰ (which equals 1), the next digit to 2¹ (which equals 2), then 2² (4), and so on.
For example, consider the binary number 1011. From right to left:
- The first (rightmost) digit is 1 × 2⁰ = 1.
- The second digit is 1 × 2¹ = 2.
- The third digit is 0 × 2² = 0.
- The fourth (leftmost) digit is 1 × 2³ = 8.
Add these values to find the total in decimal. Hence, 8 + 0 + 2 + 1 = 11. This process is the foundation of how to read binary numbers and see what they represent in our usual decimal format.
Converting Binary to Decimal
To convert a binary number to decimal, follow these steps:
- Write down each bit from right to left.
- Label each position according to increasing powers of 2 (starting from 2⁰).
- Multiply each bit by 2 raised to the power of its position.
- Add the results to get the final decimal value.
Example:
- Binary: 1011
- (1 × 2³) + (0 × 2²) + (1 × 2¹) + (1 × 2⁰)
- (1 × 8) + (0 × 4) + (1 × 2) + (1 × 1)
- 8 + 0 + 2 + 1 = 11
As a result, 1011 in binary is 11 in decimal. Therefore, converting binary to decimal becomes a simple matter of place values multiplied by powers of 2.
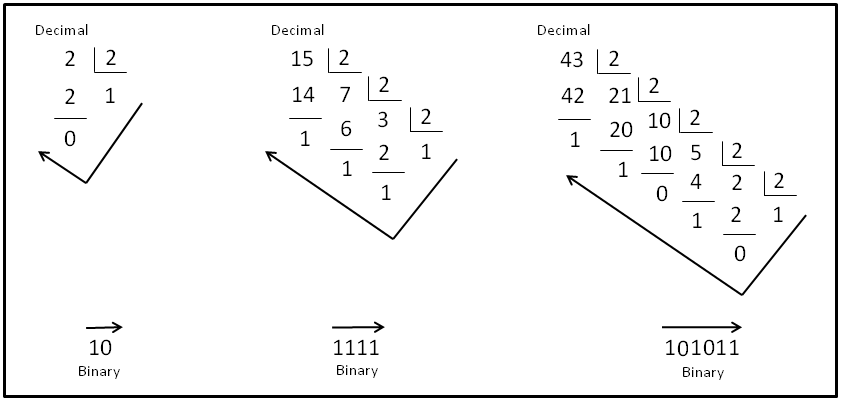
Converting Decimal to Binary
Converting a decimal number to binary can be done using repeated division by 2. The remainders form the bits of the binary number.
Steps to convert decimal 11 to binary:
- Divide 11 by 2 → quotient 5, remainder 1.
- Divide 5 by 2 → quotient 2, remainder 1.
- Divide 2 by 2 → quotient 1, remainder 0.
- Divide 1 by 2 → quotient 0, remainder 1.
Read the remainders from the last to the first. Hence, the binary number is 1011. This method is called the division method. However, some prefer subtracting powers of 2. Either way, the goal remains to capture the pattern of zeros and ones that represent a decimal number in binary form.
Comparing and Ordering Binary Numbers
To compare binary numbers, compare their lengths first. A longer binary number (with more digits) is typically larger. However, if they have the same length, compare bits from left to right until a difference appears.
For example, order the following binary numbers from smallest to largest:
- 101 (5 in decimal)
- 011 (3 in decimal)
- 110 (6 in decimal)
First, note each number’s decimal equivalent. Then, compare them by their decimal value (or directly by bits). As a result, the order is 011 (3), 101 (5), and 110 (6).
Therefore, simply line up the bits and check them in the same way you compare digits in decimal numbers. This approach reveals which binary number is bigger or smaller.
Practical Applications of Binary Numbers
Binary numbers power every computing task. For example, when sending messages over the internet, data is broken down into bits that travel through cables, wireless signals, or fiber optics. As a result, all online content ultimately depends on patterns of 0s and 1s.
Moreover, bits and bytes are used for everything from saving photos on a phone to recording music. These bits can also approximate analog data, like sound waves, by frequent sampling. Although some detail is lost when converting analog to digital, this trade-off is worth it to store, share, and process data efficiently. This process of representing complex information with bits is an example of data abstraction. It hides the intricate details but provides a straightforward way to handle information in digital devices.
Conclusion
Binary numbers play a vital role in how computers function at their deepest level. Understanding how to read, convert, and compare binary numbers helps in grasping core concepts such as data abstraction and digital storage. Therefore, bits and bytes build the backbone of simpler abstractions like text, images, and audio.
By learning how to convert binary to decimal and decimal to binary, one can see exactly how computers store and interpret values. As a result, this knowledge extends to real-world applications, where digital information constantly flows through networks, memory chips, and electronic circuits. Keep practicing with examples to gain confidence. Next time you use a phone or computer, remember that these small bits of data keep the entire digital world running smoothly.
Key Terms to Know
- Bit – Short for “binary digit,” it’s the smallest unit of data, which can be 0 or 1.
- Byte – A group of 8 bits.
- Binary Numbers – Numbers using only digits 0 and 1 (base 2).
- Decimal Numbers – Numbers using digits 0 through 9 (base 10).
- Data Abstraction – The process of reducing complexity by focusing on the main idea and hiding smaller details.
- Analog Data – Data that changes smoothly over time, such as pitch or volume in music.
- Digital Data – Data represented in discrete intervals, typically as bits (0s and 1s).
- Overflow – An error that occurs when a number is too large to fit within the allocated bits.
- Round-Off Error – A small mistake in a computed real number due to limited bits for representation.
- Sampling – Repeatedly measuring an analog signal at intervals to approximate it as digital data.
Sharpen Your Skills for AP® Computer Science Principles
Are you preparing for the AP® Computer Science Principles test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world AP® Computer Science Principles questions. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Computer Science Principles exam?
Albert has hundreds of AP® Computer Science Principles practice questions and full-length practice tests to try out.








