Absolute or global extrema are essential concepts in Calculus. They describe the highest and lowest points that a function can reach on a specific interval. Understanding how to find absolute extrema allows students to analyze functions in many real-world scenarios, such as optimizing production costs or finding peak speeds. One of the most reliable procedures for finding absolute extrema on a closed interval is known as the Candidates Test. This approach, often referred to as the “Candidates Test Calculus” method, systematically checks specific points to ensure that no maximum or minimum is overlooked. Therefore, it is helpful to know each step of this procedure.
What We Review
Understanding Absolute Extrema on a Closed Interval
Definition of Absolute (Global) Extrema
An absolute (or global) maximum is the single highest value of a function on a given interval. Similarly, an absolute (or global) minimum is the single lowest value of that function on the same interval. For example, if a function achieves its largest value at x = k, then f(k) is an absolute maximum on the interval.
Absolute extrema differ from local extrema because local maxima or minima only need to be the highest or lowest over a small neighborhood of points. However, an absolute maximum or minimum must be the highest or lowest when compared to all points in the entire domain interval.
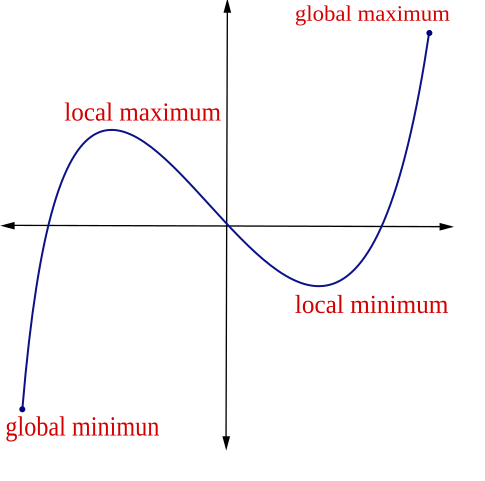
Why Endpoints Matter
A function’s endpoints on a closed interval must be checked during the process of finding absolute extrema. This is crucial because an absolute maximum or minimum can occur at interior critical points or at the boundaries x=a or x=b. Therefore, neglecting endpoint values may cause errors when trying to identify global extrema. Indeed, the candidates for absolute extrema include both the critical points and the interval’s endpoints.
The Candidates Test: Step-by-Step Overview
Identify the Function and Interval
Before beginning, confirm the function is continuous on the closed interval of interest. Keep in mind that the interval must include its endpoints, written as [a,b].
Find Critical Points
Next, compute the derivative of the function. Critical points occur where this derivative is zero or undefined. Make a list of these points that lie within [a,b].
Evaluate the Function at Each Candidate
After finding the critical points, evaluate the original function at these points. Additionally, evaluate the function at the interval’s endpoints.
Compare to Determine the Largest and Smallest Values
Finally, compare all the calculated function values. The largest value is the absolute maximum, and the smallest value is the absolute minimum on that closed interval. This process completes the Candidates Test Calculus approach for how to find absolute extrema.
Detailed Example 1
Problem Statement
Find the absolute maxima and minima of the function f(x) = x^3 - 3x^2 + 4 on the closed interval [0,3].
Step-by-Step Solution
- Identify the interval:
- The interval is [0,3].
- Find the derivative:
- f'(x) = 3x^2 - 6x.
- Solve for critical points by setting f'(x) equal to 0:
- 3x^2 - 6x = 0
- 3x(x - 2) = 0
- So, the critical points are x = 0 and x = 2.
- Evaluate the function at the critical points and endpoints:
- At x=0: f(0) = (0)^3 - 3(0)^2 + 4 = 4
- At x=2: f(2) = (2)^3 - 3(2)^2 + 4 = 8 - 12 + 4 = 0
- At x=3: f(3) = (3)^3 - 3(3)^2 + 4 = 27 - 27 + 4 = 4
- Compare the values:
- f(0) = 4, f(2) = 0, f(3) = 4.
- The largest values are 4 at x = 0 and x = 3.
- The smallest value is 0 at x = 2.
Therefore, f(x) has absolute maximum of 4 at x = 0 and x = 3, and an absolute minimum of 0 at x = 2 on [0,3].
Detailed Example 2
Problem Statement
Find the absolute maxima and minima of the function g(x) = \frac{1}{x+1} on the closed interval [0,2].
Step-by-Step Solution
- Identify the interval:
- The interval is [0,2]. The function is continuous here because x+1 never becomes zero over [0,2].
- Find the derivative:
- g'(x) = -\frac{1}{(x+1)^2}.
- Solve for critical points by setting g'(x) = 0 or checking undefined points in (0,2):
- -\frac{1}{(x+1)^2} is never 0 for real x.
- However, it is not undefined for any x in [0,2].
- Hence, there are no critical points in the open interval (0,2).
- Evaluate the function at the endpoints:
- At x=0: g(0) = \frac{1}{0+1} = 1
- At x=2: g(2) = \frac{1}{2+1} = \frac{1}{3}
- Compare the values:
- g(0) = 1 and g(2) = \frac{1}{3}.
- 1 is larger than \frac{1}{3}, so the absolute maximum is 1 at x=0.
- The absolute minimum is \frac{1}{3} at x=2.
Therefore, g(x) has an absolute maximum of 1 and an absolute minimum of \frac{1}{3} on [0,2].
Quick Reference Chart
| Term | Definition |
| Absolute Extrema | The highest or lowest values of a function on a given interval |
| Critical Point | A point where the derivative is zero or does not exist |
| Closed Interval | An interval that includes its endpoints (e.g., [a, b]) |
| Candidates Test | Method of checking all critical points and endpoints for absolute (global) extrema |
Conclusion
The Candidates Test is a powerful strategy for finding absolute extrema on a closed interval. By ensuring every critical point and both endpoints are checked, it guarantees that no global maxima or minima are missed. Moreover, this test helps demonstrate how to find absolute extrema in a systematic way. Knowing the process—along with understanding derivative rules and continuity—is critical for success in Calculus. Therefore, students benefit from practicing this method regularly to gain confidence in identifying global extrema efficiently.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 5.4 Using the First Derivative Test to Determine Relative (Local) Extrema
- 5.6 Determining Concavity of Functions over Their Domains
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








