The derivative of an inverse function is a key topic in AP® Calculus AB-BC. This concept often appears under 3.3 differentiating inverse functions. It extends the chain rule to a new level, showing how the slopes of functions and their inverses are connected. Understanding this relationship can save time in solving many calculus problems. Moreover, it reveals an elegant property: if a function rises steeply, its inverse will rise more gently, and vice versa.
What We Review
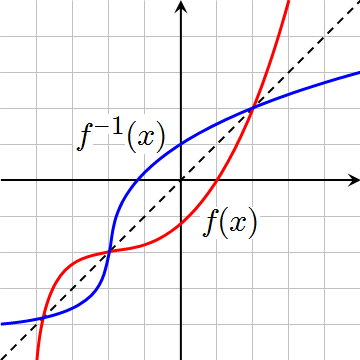
Understanding Inverse Functions
Inverse functions reverse the input and output of the original function. Therefore, if f(x) takes an input x and provides an output y, then f^{-1}(y) = x. The idea is that each output of the original function becomes the input of its inverse.
Definition of an Inverse Function
An inverse function f^{-1}(x) exists when a function f(x) is one-to-one. A one-to-one function never repeats the same y-value for two different x-values. In other words, the function passes the “horizontal line test.” This condition ensures every output corresponds to exactly one input, making reversal possible.
Domain and Range Considerations
When considering an inverse function:
- The domain of f^{-1} is the range of f.
- The range of f^{-1} is the domain of f.
This domain-range flip is important because any restriction on the original function’s domain (to keep it one-to-one) translates to a restriction on the inverse function’s range.
The Formula for the Derivative of an Inverse Function
The derivative of an inverse function follows from the chain rule. The formula is:
\frac{d}{dx} \left( f^{-1}(x) \right) = \frac{1}{f'\left( f^{-1}(x) \right)},provided f'\bigl(f^{-1}(x)\bigr) \neq 0.
Chain Rule Recap
The chain rule states that if h(x) = f(g(x)), then
h'(x) = f'(g(x)) \cdot g'(x).In the case of inverse functions, applying the chain rule to f(f^{-1}(x)) helps find \frac{d}{dx}(f^{-1}(x)).
Deriving the Formula
By definition, f(f^{-1}(x)) = x. Taking the derivative of both sides gives:
f'\bigl(f^{-1}(x)\bigr) \cdot \frac{d}{dx}\bigl(f^{-1}(x)\bigr) = 1.Solving for \frac{d}{dx}(f^{-1}(x)) leads to:
\frac{d}{dx}\bigl(f^{-1}(x)\bigr) = \frac{1}{f'\bigl(f^{-1}(x)\bigr)}.Step-by-Step Example 1
Consider the function f(x) = x^2 + 1, defined only for x \geq 0 so it remains one-to-one.
- Find the inverse f^{-1}(x).
- Let y = x^2 + 1.
- Swap x and y: x = y^2 + 1.
- Solve for y: x - 1 = y^2y = \sqrt{x - 1}, keeping y \geq 0 because the original function was restricted to x \ge 0.
- Therefore, f^{-1}(x) = \sqrt{x - 1}.
- Compute f'\bigl(x\bigr).
- f(x) = x^2 + 1, sof'(x) = 2x.
- Apply the derivative of an inverse function formula at a specific point, say x = 5.
- First, determine f^{-1}(5): f^{-1}(5) = \sqrt{5 - 1} = \sqrt{4} = 2.
- Next, evaluate f'(f^{-1}(5)): f'(2) = 2(2) = 4.
- Finally, plug into the formula: \frac{d}{dx} \left( f^{-1}(5) \right) = \frac{1}{4}.
Hence, the slope of the inverse function at x = 5 is \frac{1}{4}.
Step-by-Step Example 2
Next, explore f(x) = 3x^3 + 2. This polynomial is one-to-one over all real numbers because the cubic function keeps increasing without repeating any outputs.
- Find the inverse value for a particular input. Directly finding the entire inverse expression is possible but often not necessary for computing the derivative at one point. Suppose the goal is to find \frac{d}{dx}\bigl(f^{-1}(x)\bigr) at x = 29.
- First, find f^{-1}(29) by solving 3x^3 + 2 = 29.
- 3x^3 = 27
- x^3 = 9
- x = \sqrt[3]{9}. Thus, f^{-1}(29) = \sqrt[3]{9}.
- Determine f'(x).
- Since f(x) = 3x^3 + 2, the derivative is f'(x) = 9x^2.
- Evaluate f'\bigl(f^{-1}(29)\bigr).
- Substitute x = \sqrt[3]{9} into f'(x) = 9x^2: f'(\sqrt[3]{9}) = 9\left(\sqrt[3]{9}\right)^2.
- Use the derivative of an inverse function formula.
- \frac{d}{dx}\bigl(f^{-1}(29)\bigr) = \frac{1}{f'(\sqrt[3]{9})} = \frac{1}{9\left(\sqrt[3]{9}\right)^2}.
This result demonstrates the importance of correct substitution into f'\bigl(f^{-1}(x)\bigr).
Tips and Common Pitfalls
- Always confirm the function is one-to-one before discussing its inverse.
- Avoid forgetting to restrict the domain to ensure an inverse function exists.
- Use the formula \frac{1}{f'\bigl(f^{-1}(x)\bigr)}, not \frac{1}{f'(x)}. Substitution errors are a frequent source of mistakes.
- Watch out for points where f'(x) = 0. At those locations, the inverse function’s derivative does not exist (or the inverse may not exist there).
- Carefully note when f'(f^{-1}(x)) might be zero or undefined.
Quick Reference Chart
| Term | Definition or Key Feature |
| Derivative of an Inverse | \frac{d}{dx} \bigl(f^{-1}(x)\bigr) = \frac{1}{f'\bigl(f^{-1}(x)\bigr)} |
| Inverse Function f^{-1} | Reverses the input-output mapping of f(x), swapping domain and range. |
| One-to-One | A function with no repeated y-values, enabling an inverse. |
| Chain Rule Components | If h(x) = f(g(x)), then h'(x) = f'(g(x)) \cdot g'(x). |
Conclusion
Students often find the derivative of an inverse function less daunting once the chain rule connection is clear. Recognizing that \frac{d}{dx}(f^{-1}(x)) depends on evaluating f'(x) at f^{-1}(x) provides a straightforward procedure. Above all, the essential key is substitution: inserting the correct x-value into f'\bigl(f^{-1}(x)\bigr) to avoid confusion. This technique is tested under 3.3 differentiating inverse functions in AP® Calculus AB-BC and aligns with FUN-3.E.1 in the curriculum. Mastering these steps lays a strong foundation for additional topics, including related rates and advanced applications of derivatives.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








