What We Review
Introduction
Inverse trigonometric functions allow us to reverse the process of sine, cosine, tangent, and other trigonometric functions. They are crucial in AP® Calculus AB-BC when analyzing functions and solving real-world problems. Therefore, understanding the derivative of inverse trig functions is essential. In many courses, 3.4 differentiating inverse trig functions focuses on applying formulas along with the chain rule to find slopes of curves involving these functions.
This article will explore the derivative of sin inverse, the derivative of inverse cosine, the derivative of inverse tan, and more. It will also explain how to handle composite functions, such as the derivative of inverse tan 2x, using step-by-step solutions and clear examples.
What Are Inverse Trig Functions?
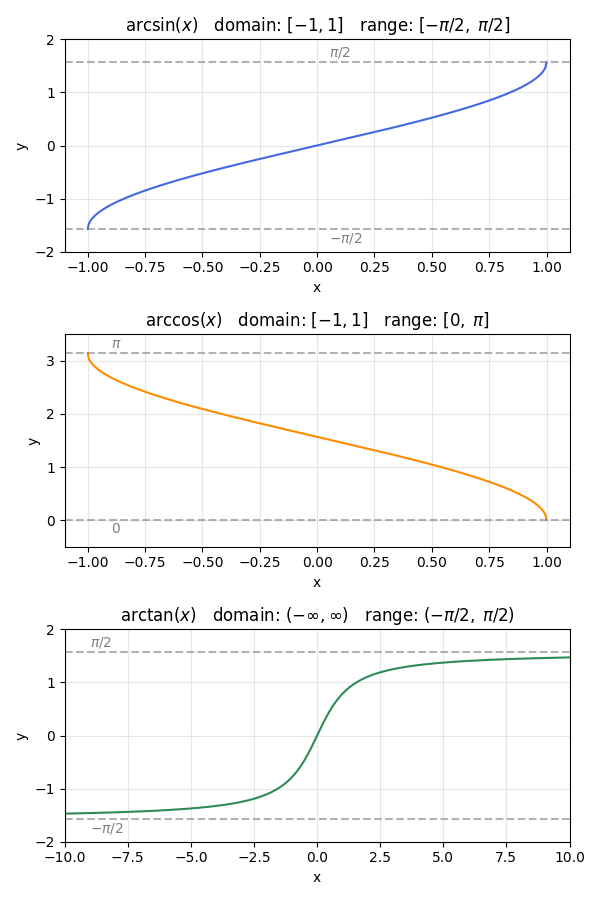
Definition and Meaning
Inverse trig functions “undo” the original trigonometric functions. For instance, \sin^{-1}(x) is the inverse of \sin(x). Similarly, \cos^{-1}(x) undoes \cos(x), and \tan^{-1}(x) undoes \tan(x).
However, each inverse trig function has a specific domain and range to maintain a one-to-one relationship.
- \sin^{-1}(x) has a domain of -1 \le x \le 1 and a range of -\frac{\pi}{2} \le y \le \frac{\pi}{2}.
- \cos^{-1}(x) has a domain of -1 \le x \le 1 and a range of 0 \le y \le \pi.
- \tan^{-1}(x) has a domain of all real numbers and a range of -\frac{\pi}{2} < y < \frac{\pi}{2}.
Quick Conceptual Check
Consider \sin(x) = \frac{\sqrt{2}}{2}. The inverse sine function solves for the angle, so \sin^{-1}\left(\frac{\sqrt{2}}{2}\right) equals \frac{\pi}{4} (or 45 degrees). Thus, the inverse process recovers the angle from the sine value.
Derivative of Inverse Trig Functions: Formulas
There are standard results for the derivative of inverse trig functions. Recognizing these formulas is key to 3.4 differentiating inverse trig functions.
Derivative of \sin^{-1}(x) (Derivative of Sin Inverse)
\frac{d}{dx} \sin^{-1}(x) = \frac{1}{\sqrt{1 - x^2}}This result often appears in integration and related rates problems.
Derivative of \cos^{-1}(x) (Derivative of Inverse Cosine)
\frac{d}{dx} \cos^{-1}(x) = -\frac{1}{\sqrt{1 - x^2}}Notice the only difference is the negative sign, which comes from the properties of the cosine function.
Derivative of \tan^{-1}(x) (Derivative of Inverse Tan)
\frac{d}{dx} \tan^{-1}(x) = \frac{1}{1 + x^2}This frequently arises in calculus problems because \tan^{-1}(x) appears in integrals and in certain optimization scenarios.
Other Inverse Trig Functions (arcsec, arccsc, arccot)
- \frac{d}{dx} \csc^{-1}(x) = -\frac{1}{|x|\sqrt{x^2 - 1}}
- \frac{d}{dx} \sec^{-1}(x) = \frac{1}{|x|\sqrt{x^2 - 1}}
- \frac{d}{dx} \cot^{-1}(x) = -\frac{1}{1 + x^2}
Noticing patterns is straightforward: the negative signs in certain derivatives match the sign changes in their original trig functions.
Applying the Chain Rule: 3.4 Differentiating Inverse Trig Functions
Reminder of the Chain Rule
The chain rule states: \frac{d}{dx} \bigl[f(g(x))\bigr] = f'(g(x)) \times g'(x). When dealing with a composite function, identify the “inner” function and the “outer” function to apply this rule properly.
Combining the Chain Rule with Inverse Trig Functions
When the inside of an inverse trig function is more complex than x, multiply the standard derivative of the outer function by the derivative of that inside function.
For instance, if given \tan^{-1}(2x), or the derivative of inverse tan 2x, remember: \frac{d}{dx} \tan^{-1}(2x) = \frac{1}{1 + (2x)^2} \times 2. Thus, the chain rule captures the behavior of whatever is inside the inverse trigonometric function.
Step-by-Step Examples
Example 1: Derivative of \sin^{-1}(3x)
- Identify the outer and inner functions:
- Outer function: \sin^{-1}(u)
- Inner function: u = 3x
- Apply the chain rule and the derivative of \sin^{-1}(x): \frac{d}{dx}\sin^{-1}(3x) = \frac{1}{\sqrt{1 - (3x)^2}} \times 3
- Simplify the result: \frac{3}{\sqrt{1 - 9x^2}}.
Therefore, the derivative is: \frac{d}{dx} \sin^{-1}(3x) = \frac{3}{\sqrt{1 - 9x^2}}.
Example 2: Derivative of \tan^{-1}(2x) (Derivative of Inverse Tan 2x)
- Recognize the outer (inverse tangent) and inner (2x) functions.
- Use the formula \frac{d}{dx} \tan^{-1}(u) = \frac{1}{1 + u^2}, then multiply by \frac{d}{dx}(2x) = 2.
- Combine to get the final simplification: \frac{d}{dx}\tan^{-1}(2x) = \frac{1}{1 + (2x)^2} \times 2= \frac{2}{1 + 4x^2}.
Hence, the derivative of inverse tan 2x is \frac{2}{1 + 4x^2}.
Example 3: Derivative of \csc^{-1}(x/2) (Derivative of Inverse Csc)
- Identify the outer inverse trig function \csc^{-1}(u) and the inner function u = x/2.
- Recall the formula: \frac{d}{dx} \csc^{-1}(u) = -\frac{1}{|u|\sqrt{u^2 - 1}}. Then multiply by the derivative of u = x/2, which is \frac{1}{2}.
- Write out and simplify: \frac{d}{dx}\csc^{-1}\left(\frac{x}{2}\right) = -\frac{1}{\left|\frac{x}{2}\right|\sqrt{\left(\frac{x}{2}\right)^2 - 1}} \times \frac{1}{2}.
- Simplify step by step:
- \left|\frac{x}{2}\right| = \frac{|x|}{2}
- \left(\frac{x}{2}\right)^2 = \frac{x^2}{4}
- So the derivative becomes: -\frac{1}{\frac{|x|}{2} \sqrt{\frac{x^2}{4} - 1}} \times \frac{1}{2}.
- Which can be rewritten as: -\frac{1}{2} \cdot \frac{1}{\frac{|x|}{2} \sqrt{\frac{x^2}{4} - 1}}= -\frac{1}{|x|\sqrt{\frac{x^2}{4} - 1}}.
- Simplify step by step:
Therefore, \frac{d}{dx} \csc^{-1}\left(\frac{x}{2}\right) = -\frac{1}{|x|\sqrt{\frac{x^2}{4} - 1}}.
Quick Reference Chart (Important Vocabulary and Definitions)
| Term | Definition |
| Inverse Trig | Functions that reverse the process of sine, cosine, tangent, etc. |
| Domain/Range | The set of possible x-values (domain) and resulting y-values (range) for a function |
| Chain Rule | A method to differentiate composite functions: \frac{d}{dx}[f(g(x))] = f'(g(x)) \times g'(x) |
| \sin^{-1}(x) | Inverse sine, also written as arcsin(x) |
| \cos^{-1}(x) | Inverse cosine, also written as arccos(x) |
| \tan^{-1}(x) | Inverse tangent, also written as arctan(x) |
| \csc^{-1}(x) | Inverse cosecant, also written as arccsc(x) |
Conclusion
Inverse trigonometric functions form an essential part of calculus, especially when exploring 3.4 differentiating inverse trig functions. The key to finding the derivative of inverse trig functions lies in memorizing the standard formulas and carefully applying the chain rule when the inside of the function is more complicated than x.
Careful attention to signs, absolute values, and the domain of each function helps avoid mistakes. Therefore, always check each step when finding the derivative of sin inverse, derivative of inverse tan, derivative of inverse cosine, or derivative of inverse csc. This extra caution ensures precision in problem-solving. By practicing each formula with examples such as the derivative of inverse tan 2x, learners can build confidence and excel in AP® Calculus examinations.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








