The polar axis sets the stage for understanding how angles and distances define points in the plane. When a point is described by a distance r from the origin (or pole) and an angle \theta from the polar axis, it is said to be in polar coordinates. This way of describing points is often used in advanced calculus and physics to simplify certain problems, especially when working with the derivative of polar equation forms.
However, finding the derivative of polar equations is also important in AP® Calculus AB-BC. Derivatives help determine slopes, tangents, and curvature for curves described in polar form. This article explains how to convert polar to rectangular coordinates and how to find both the first and second derivatives for these polar equations. It also includes a quick reference chart to reinforce key vocabulary.
What We Review
Converting Polar to Rectangular Coordinates
Many problems require switching from polar form to rectangular form. This process is called converting polar to rectangular coordinates. Remember these relationships:
- x = r \cos(\theta)
- y = r \sin(\theta)
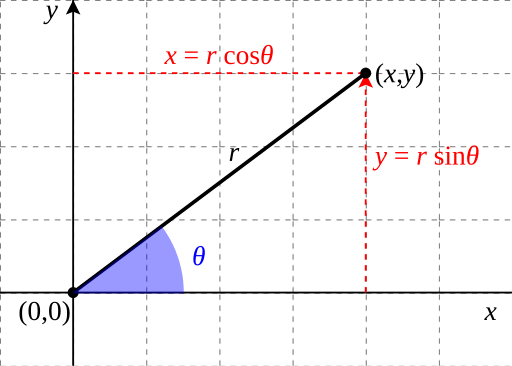
Finding the First Derivative of Polar Equations
The derivative of polar equation expressions is useful for calculating the slope of a curve in rectangular form. Consequently, knowing how r changes with \theta is the first step.
General Formulas
- \frac{dr}{d\theta} measures how r depends on \theta.
- \frac{dx}{d\theta} = \frac{dr}{d\theta} \cos(\theta) - r \sin(\theta)
- \frac{dy}{d\theta} = \frac{dr}{d\theta} \sin(\theta) + r \cos(\theta)
- \frac{dy}{dx} = \frac{dy}{d\theta}\div\frac{dx}{d\theta}
Step-by-Step Example: dy/dx for a Given r(\theta)
Consider r(\theta) = 3 + 2 \sin(\theta).
- Find \frac{dr}{d\theta}.
- \frac{dr}{d\theta} = 2 \cos(\theta)
- Compute \frac{dx}{d\theta}:
- \frac{dx}{d\theta} = \left(2 \cos(\theta)\right) \cos(\theta) - (3 + 2 \sin(\theta)) \sin(\theta)
- Simplify step by step:
- \frac{dx}{d\theta} = 2 \cos^2(\theta) - 3 \sin(\theta) - 2 \sin^2(\theta)
- Compute \frac{dy}{d\theta}:
- \frac{dy}{d\theta} = \left(2 \cos(\theta)\right) \sin(\theta) + (3 + 2 \sin(\theta)) \cos(\theta)
- Simplify:
- \frac{dy}{d\theta} = 2 \sin(\theta)\cos(\theta) + 3 \cos(\theta) + 2 \sin(\theta)\cos(\theta)
- \frac{dy}{d\theta} = 4 \sin(\theta)\cos(\theta) + 3 \cos(\theta)
- Divide to find \frac{dy}{dx}:
- \frac{dy}{dx} = \frac{4 \sin(\theta)\cos(\theta) + 3 \cos(\theta)}{2 \cos^2(\theta) - 3 \sin(\theta) - 2 \sin^2(\theta)}
- Check for places where \frac{dx}{d\theta} = 0, because these indicate vertical tangents.
Practice Problem: First Derivative
Given r(\theta) = 2\theta + 1, find \frac{dy}{dx}.
Step-by-Step Solution:
- Find \frac{dr}{d\theta}:
- \frac{dr}{d\theta} = 2
- Compute \frac{dx}{d\theta}:
- \frac{dx}{d\theta} = 2 \cos(\theta) - (2\theta + 1) \sin(\theta)
- Compute \frac{dy}{d\theta}:
- \frac{dy}{d\theta} = 2 \sin(\theta) + (2\theta + 1) \cos(\theta)
- Find the quotient:
- \frac{dy}{dx} = \frac{2 \sin(\theta) + (2\theta + 1) \cos(\theta)}{2 \cos(\theta) - (2\theta + 1) \sin(\theta)}
How to Take the Second Derivative of Polar Equations
The second derivative, \frac{d^2 y}{dx^2}, provides insight into the curvature or concavity of the curve. It follows a straightforward chain rule process in polar form.
Formula for \frac{d^2 y}{dx^2}
The general approach is:
- \frac{d^2 y}{dx^2} = \frac{\frac{d}{d\theta}\left(\frac{dy}{dx}\right)}{\frac{dx}{d\theta}}
This means the derivative of \frac{dy}{dx} with respect to \theta, divided by \frac{dx}{d\theta}.
Step-by-Step Example: \frac{d^2 y}{dx^2} for the Same r(\theta)
Continue with r(\theta) = 3 + 2 \sin(\theta).
- Start with \frac{dy}{dx} found earlier:
- \frac{dy}{dx} = \frac{4 \sin(\theta)\cos(\theta) + 3 \cos(\theta)}{2 \cos^2(\theta) - 3 \sin(\theta) - 2 \sin^2(\theta)}
- Differentiate \frac{dy}{dx} with respect to \theta. This involves quotient rule:
- \frac{d}{d\theta}\left(\frac{dy}{dx}\right) = \frac{\left(\text{denominator}\right)\left(\text{derivative of numerator}\right) - \left(\text{numerator}\right)\left(\text{derivative of denominator}\right)}{\left(\text{denominator}\right)^2}
- Divide the result by \frac{dx}{d\theta}.
- Recognize that the expression can become quite complex. Therefore, it is helpful to simplify carefully, watching for any common factors.
- Understand that the sign of this result indicates concavity: positive for concave up, negative for concave down.
Practice Problem: Second Derivative
Use the first derivative result for r(\theta) = 2\theta + 1 to find \frac{d^2 y}{dx^2}.
Step-by-Step Solution:
- Recall \frac{dy}{dx} = \frac{2 \sin(\theta) + (2\theta + 1) \cos(\theta)}{2 \cos(\theta) - (2\theta + 1) \sin(\theta)}.
- Apply the quotient rule with respect to \theta.
- Simplify the numerator and the denominator.
- Divide this derivative by \frac{dx}{d\theta} = 2 \cos(\theta) - (2\theta + 1) \sin(\theta).
- Carefully look for any overlooked terms and combine like terms for the final expression.
Key Takeaways and Tips
- Keep track of \frac{dr}{d\theta}, \frac{dx}{d\theta}, and \frac{dy}{d\theta}.
- Always check points where \frac{dx}{d\theta} = 0, because these suggest vertical tangents.
- Use standard polar to rectangular coordinates conversions consistently.
- Practice differentiating step by step to reduce errors.
- Remember that the derivative of polar equation functions often requires patience with algebra.
Quick Reference Chart
| Vocabulary | Definition |
| Polar Axis | The reference line from which θ is measured. Often corresponds to the x-axis in rectangular coordinates. |
| r | The distance from the origin (pole) to a point. |
| θ (theta) | The angle measured from the polar axis to the line segment connecting the point to the origin. |
| dr/dθ | The rate of change of r with respect to θ. |
| dx/dθ, dy/dθ | The rates of change of x and y with respect to θ, respectively. Used to find the slope in polar coordinates. |
| dy/dx | The first derivative of the polar curve when expressed in rectangular form (y as a function of x). |
| d²y/dx² | The second derivative, providing information about curvature and concavity. |
Conclusion
Finding the derivative of polar equation forms requires understanding how r and \theta relate and how these translate into x and y. Moreover, converting polar to rectangular coordinates is often the first step in tackling calculus problems. Knowing how to take the second derivative of polar equations deepens knowledge of curvature and helps analyze the geometry of these curves. Consistent practice, careful algebra, and diligent application of chain rule concepts are the keys to success.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








