Understanding how to differentiate a polynomial function is a key part of success in AP® Calculus AB-BC. This topic aligns with the standards FUN-3.A.2 and FUN-3.A.3, which stress the importance of derivative rules. Therefore, mastering these rules, including the derivative of polynomial functions, sets a solid foundation for more advanced calculus concepts. This review covers the main rules—including sum, difference, constant multiple, and the power rule—and provides step by step example problems to build confidence.
What We Review
Understanding Polynomials
A polynomial is a function consisting of terms that are added or subtracted together. Each term has a coefficient (a constant factor) and a variable raised to a non-negative integer exponent.
For example, p(x) = 5x^3 + 2x^2 - x + 7 is a polynomial.
- The coefficients are 5, 2, -1, and 7.
- The terms are 5x^3, 2x^2, -x, and 7.
- The highest exponent is 3, so the degree of the polynomial is 3.
When finding the derivative of a polynomial, the goal is to calculate the slope of its tangent line at any point on the curve. Although polynomials can look complicated, it is often straightforward to apply derivative rules.
The Sum, Difference, and Constant Multiple Rules
The derivative of a polynomial often involves combining simpler rules:
- Sum Rule: \frac{d}{dx} \big( f(x) + g(x) \big) = f'(x) + g'(x)
- Difference Rule: \frac{d}{dx} \big( f(x) - g(x) \big) = f'(x) - g'(x)
- Constant Multiple Rule: \frac{d}{dx} \big( c \cdot f(x) \big) = c \cdot f'(x)
These rules simplify the process of taking derivatives term by term. By treating each term separately, one can add, subtract, or factor out constants without much difficulty.
For instance, if h(x) = 3f(x) - 7g(x), then h'(x) = 3f'(x) - 7g'(x).
The Power Rule
The power rule is vital for finding the derivative of a polynomial. It states: \frac{d}{dx}(x^n) = n \cdot x^{n-1}
This rule indicates that when differentiating x^n, multiply by the exponent and reduce the exponent by one.
Therefore, if f(x) = x^3, thenf'(x) = 3x^2.
The power rule is often applied to every term in a polynomial. This makes it one of the most efficient ways to find the derivative of polynomial expressions.
Combining Derivative Rules for Polynomial Functions
Differentiating polynomials typically requires using a combination of the sum, difference, constant multiple, and power rules:
- Identify each term in the polynomial.
- Apply the constant multiple rule if a term has a numerical coefficient.
- Use the power rule on each variable factor.
- Add or subtract the derivatives of each term as required.
Always watch for common pitfalls, such as forgetting to reduce the exponent or neglecting to multiply by the original constant. However, careful attention to detail avoids these mistakes.
Example Problems with Step-by-Step Solutions
A. Example 1: Simple Polynomial
- Problem Statement
- Find the derivative of p(x) = 4x^2 - 3x + 6.
- Step-by-Step Solution
- First, separate each term: 4x^2, -3x, and 6.
- Apply the power rule to 4x^2: \frac{d}{dx}(4x^2) = 4 \cdot 2x^{2-1} = 8x.
- Apply the power rule to -3x: \frac{d}{dx}(-3x) = -3 \cdot 1 \cdot x^{1-1} = -3.
- The derivative of a constant 6 is 0.
- Combine these results to get the final answer: p'(x) = 8x - 3.
The image below helps connect the visual of this function and its derivative.
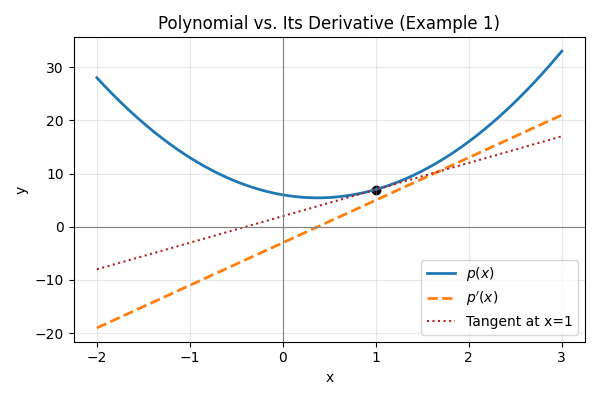
B. Example 2: More Advanced Polynomial
- Problem Statement
- Find the derivative of q(x) = 2x^5 - 5x^3 + 10x - 1.
- Step-by-Step Solution
- Identify each term: 2x^5, -5x^3, 10x, and -1.
- Take the derivative term by term using the power rule:
- \frac{d}{dx}(2x^5) = 2 \cdot 5x^{5-1} = 10x^4
- \frac{d}{dx}(-5x^3) = -5 \cdot 3x^{3-1} = -15x^2
- \frac{d}{dx}(10x) = 10 \cdot 1 \cdot x^{1-1} = 10
- \frac{d}{dx}(-1) = 0
- Add them all together: q'(x) = 10x^4 - 15x^2 + 10.
Quick Reference Chart
Below is a short guide to reinforce key terms and definitions:
| Vocabulary | Definition or Feature |
| Polynomial | A function made up of terms combined by addition or subtraction. No negative or fractional exponents. |
| Coefficient | The numerical factor multiplied by a variable in a term. |
| Derivative | The slope of the tangent line to a function at a given point. |
| Power Rule | If f(x) = x^n, then f'(x) = n \cdot x^{n-1}. |
| Sum and Difference Rules | \frac{d}{dx}(f(x) \pm g(x)) = f'(x) \pm g'(x). |
| Constant Multiple Rule | \frac{d}{dx}(c \cdot f(x)) = c \cdot f'(x). |
Conclusion
In summary, the derivative of polynomial functions is found by applying the sum, difference, constant multiple, and power rules. These rules ensure efficiency when dealing with various terms in a polynomial. Carefully working through each term step by step avoids careless errors, and the final answer follows naturally.
Understanding these concepts also satisfies important AP® Calculus AB-BC goals, particularly FUN-3.A.2 and FUN-3.A.3. Moreover, knowing these basics leads to confidence in future topics, such as the chain rule and product rule. Ultimately, a strong command of these rules creates a solid platform for exploring more advanced calculus subjects.
Remember, regular practice is key. Therefore, consider revisiting each rule frequently and trying additional questions to strengthen skills.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








