What We Review
Introduction
Understanding the derivative of sin, cos, tan, sec, csc, and cot is essential for anyone studying AP® Calculus AB-BC. These functions appear frequently in higher-level math and physics, helping model periodic motion, wave behavior, and more. Therefore, knowing how to handle the derivative of tangent, derivative of cotangent, and other trig functions will simplify many calculus problems. Mastering these formulas also opens doors to solving more complex equations, especially when combined with standard trigonometric identities.
This article covers the derivative of sin, cos, tan, sec, csc, and cot, step by step. It also shows how to apply trigonometric identities when dealing with more challenging functions. A quick reference chart of important definitions is provided at the end.
Basic Trigonometric Derivatives (Sine and Cosine)
It is helpful to start with the two most familiar trigonometric derivatives: sine and cosine. The derivative formulas are: d/dx[\sin(x)] = \cos(x) and d/dx[\cos(x)] = -\sin(x).
These two results should be memorized, as they are building blocks for the derivative of tan, cot, sec, and csc. In many problems, recognizing these core derivatives will allow faster and more accurate work.
Example with Step-by-Step Solution
Differentiate the function f(x) = \sin(x) - 2\cos(x).
- Apply the rule that the derivative of \sin(x) is \cos(x).
- Use the fact that the derivative of \cos(x) is -\sin(x).
- Note the constant multiplier -2. The derivative of -2\cos(x) is -2 \cdot (-\sin(x)) = 2\sin(x).
- Therefore, f'(x) = \cos(x) + 2\sin(x).
Derivative of Tangent
The derivative of tangent often arises in optimization and related rates. Recall the definition \tan(x) = \sin(x) / \cos(x).
Using the quotient rule or trigonometric identities, it is found that: d/dx[\tan(x)] = \sec^2(x).
Therefore, the derivative of tangent can also be remembered using the identity 1 + \tan^2(x) = \sec^2(x).
Below is a visual of tangent graphed with its derivative on a small window:
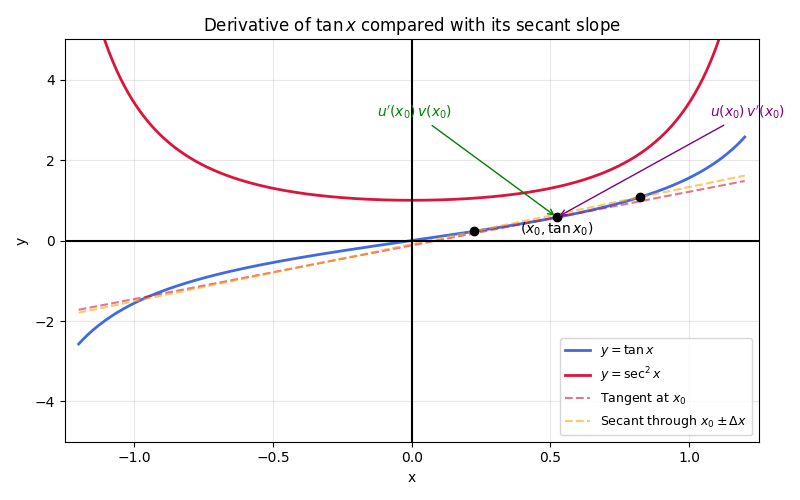
Example with Step-by-Step Solution
Differentiate the function f(x) = 3\tan(x).
- Factor out the constant 3.
- Recall that d/dx[\tan(x)] = \sec^2(x).
- Multiply the result by 3.
- Hence, f'(x) = 3\sec^2(x).
Derivative of Cotangent
Next, consider the derivative of cotangent. This function can be written as \cot(x) = \cos(x) / \sin(x) or 1 / \tan(x). By applying the quotient rule or by reasoning about the reciprocal relationship, the result is: d/dx[\cot(x)] = -\csc^2(x).
Recognizing the negative sign is vital for correct answers on quizzes and exams.
Example with Step-by-Step Solution
Differentiate the function f(x) = 2 - 4\cot(x).
- The derivative of the constant 2 is 0.
- Focus on the term -4\cot(x).
- Using linearity, factor out -4.
- The derivative of \cot(x) is -\csc^2(x).
- Combine: -4 \cdot \bigl(-\csc^2(x)\bigr) = 4\csc^2(x).
- Therefore, f'(x) = 4\csc^2(x).
Derivative of Secant
The derivative of secant is also linked to sine and cosine. Recall \sec(x) = 1 / \cos(x). Using the chain rule gives: d/dx[\sec(x)] = \sec(x)\tan(x).
When dealing with the derivative of secant, remembering the product \sec(x)\tan(x) saves time.
Example with Step-by-Step Solution
Differentiate the function f(x) = 5\sec(x).
- Factor out the constant 5.
- The derivative of \sec(x) is \sec(x)\tan(x).
- Multiply by 5 to get 5\sec(x)\tan(x).
- Thus, f'(x) = 5\sec(x)\tan(x).
Derivative of Cosecant
Finally, consider the derivative of csc. Recall \csc(x) = 1 / \sin(x). By the chain rule, the result is: d/dx[\csc(x)] = -\csc(x)\cot(x).
Noting the negative sign is important here as well.
Example with Step-by-Step Solution
Differentiate the function f(x) = -\csc(x).
- Factor out the negative sign.
- The derivative of \csc(x) is -\csc(x)\cot(x).
- Combine negatives: the overall sign of the derivative becomes positive \csc(x)\cot(x).
- Hence, f'(x) = \csc(x)\cot(x).
Using Trig Identities for More Complex Scenarios
Sometimes, extra steps are beneficial before taking a derivative. For instance, Pythagorean identities like \sec^2(x) - \tan^2(x) = 1 enable simplification. These identities can help rewrite expressions into more familiar forms. Therefore, it is wise to check if an expression can be simplified first.
Example with Step-by-Step Solution
Differentiate f(x) = \sec(x) + \tan(x) in one expression.
- Recall d/dx[\sec(x)] = \sec(x)\tan(x).
- Remember d/dx[\tan(x)] = \sec^2(x).
- Differentiate each term:
- The derivative of \sec(x) is \sec(x)\tan(x).
- The derivative of \tan(x) is \sec^2(x).
- Add them together: f'(x) = \sec(x)\tan(x) + \sec^2(x).
Quick Reference Vocabulary and Definitions
| Term | Definition or Key Point |
| Sine (sin) | A fundamental trig function. d/dx[\sin(x)] = \cos(x). |
| Cosine (cos) | A fundamental trig function. d/dx[\cos(x)] = -\sin(x). |
| Tangent (tan) | \tan(x) = \sin(x)/\cos(x). d/dx[\tan(x)] = \sec^2(x). |
| Cotangent (cot) | \cot(x) = \cos(x)/\sin(x). d/dx[\cot(x)] = -\csc^2(x). |
| Secant (sec) | \sec(x) = 1/\cos(x). d/dx[\sec(x)] = \sec(x)\tan(x). |
| Cosecant (csc) | \csc(x) = 1/\sin(x). d/dx[\csc(x)] = -\csc(x)\cot(x). |
Conclusion
All six derivatives—derivative of sin, derivative of cos, derivative of tangent, derivative of cotangent, derivative of secant, and derivative of csc—are crucial in calculus. They form the foundation of many applications, such as finding maxima and minima in trigonometric functions or solving advanced trigonometric integrals. Therefore, consistent practice is recommended.
Combining these results with known trigonometric identities ensures more flexible problem-solving. Building comfort with these formulas and identities paves the way for success in AP® Calculus and beyond.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








