Derivatives measure how a function changes as its input changes. They form the backbone of AP® Calculus AB and BC. Therefore, gaining confidence with key differentiation rules is crucial for success. In “derivative practice problems,” it helps to remember each rule’s formula and practice applying it in diverse situations. This article highlights the most common rules. Then, it walks through two examples—one focusing on the “derivative of xsinx,” and another focusing on “chain rule derivative practice problems.” By the end, there will be a quick reference chart to reinforce essential vocabulary.

Review of Key Differentiation Rules

Derivatives follow standardized formulas that streamline calculations. However, knowing which rule to use comes with practice. Next, see how each rule works and try the practice problem to apply it.

Power Rule

The power rule is often the first rule learned:

\frac{d}{dx}[x^n] = n \cdot x^{n-1}

This rule is especially useful for polynomials. For instance, if the function is f(x) = x^3, then f'(x) = 3x^2.

Practice Problem (Power Rule)

• Find the derivative of f(x) = 5x^4.

Step-by-Step Solution:

1. Identify that n=4 and the coefficient is 5.
2. Apply the power rule: \frac{d}{dx} [x^n] = n \cdot x^{n-1}.
3. Combine the constant with the new exponent: \frac{d}{dx}[5x^4] = 5 \times 4 \times x^{3} = 20x^3.
4. Final answer: 20x^3.

Product Rule

When two functions multiply, the derivative is calculated with the product rule:

\frac{d}{dx}[f \cdot g] = f' \cdot g + f \cdot g'

This formula applies to polynomials, trigonometric functions, or any combination. In “derivative practice problems,” this rule helps to simplify lengthy functions multiplied together.

Practice Problem (Product Rule)

• Find the derivative of f(x) = (2x+1)(x^2).

Step-by-Step Solution:

1. Let f_1(x) = 2x+1 and f_2(x) = x^2.
2. Compute f'_1(x) and f'_2(x).
   • f'_1(x) = 2
   • f'_2(x) = 2x
3. Apply the product rule: \frac{d}{dx}[f_1 \cdot f_2] = f'_1 \cdot f_2 + f_1 \cdot f'_2.
4. Substitute: = 2 \cdot x^2 + (2x+1)\cdot 2x.
5. Simplify: = 2x^2 + 4x^2 + 2x = 6x^2 + 2x.

Chain Rule

The chain rule applies to composite functions, such as \sin(x^2). Its formula is:

\frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)

Because many “chain rule derivative practice problems” involve multiple layers, it is helpful to label outer and inner functions clearly.

Practice Problem (Chain Rule)

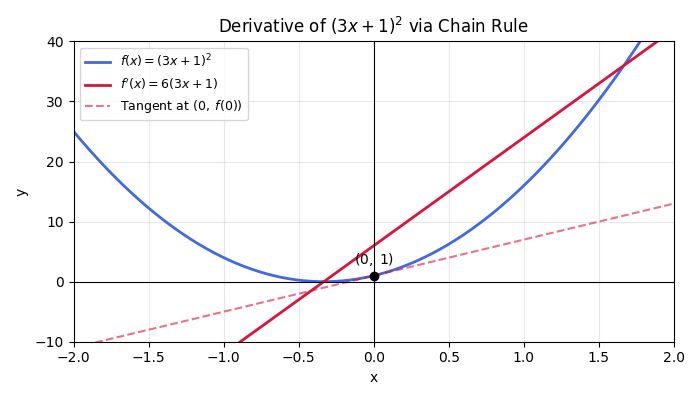
• Find the derivative of f(x) = (3x+1)^2.

Step-by-Step Solution:

1. Let the outer function be F(u) = u^2 and the inner function be u = 3x+1.
2. Compute F'(u) and u'(x):
   • F'(u) = 2u
   • u'(x) = 3
3. Apply the chain rule: \frac{d}{dx}[F(u)] = F'(u) \cdot u'(x).
4. Substitute back: = 2(3x+1) \cdot 3.
5. Simplify: = 6(3x+1) = 18x + 6.

Quotient Rule (Optional Review)

For dividing one function by another, use the quotient rule:

\frac{d}{dx}\bigg[\frac{f}{g}\bigg] = \frac{f' \cdot g - f \cdot g'}{g^2}

This rule can simplify “derivative practice problems” that require precise handling of fractions.

Practice Problem (Quotient Rule)

• Find the derivative of f(x) = \frac{x^2}{2x+1}.

Step-by-Step Solution:

1. Let f(x) = x^2 and g(x) = 2x+1.
2. Compute f'(x) and g'(x):
   • f'(x) = 2x
   • g'(x) = 2
3. Apply the quotient rule: \frac{d}{dx}\bigg[\frac{f}{g}\bigg] = \frac{f' \cdot g - f \cdot g'}{g^2}.
4. Substitute: = \frac{(2x)(2x+1) - (x^2)(2)}{(2x+1)^2}.
5. Simplify: = \frac{4x^2 + 2x - 2x^2}{(2x+1)^2} = \frac{2x^2 + 2x}{(2x+1)^2}.

Example 1: Derivative of x sin x

This example focuses on the “derivative of xsinx.” Notice that both x and \sin(x) are separate functions, so use the product rule.

Step-by-Step Solution:

1. Label f_1(x) = x and f_2(x) = \sin(x).
2. Find f'_1(x) = 1 and f'_2(x) = \cos(x).
3. Apply the product rule: \frac{d}{dx}[x \sin(x)] = (1)\sin(x) + x \cos(x).
4. Combine terms: = \sin(x) + x \cos(x).

Common Pitfalls:

• Forgetting that \frac{d}{dx}[x] = 1 instead of 0.
• Mixing up \sin(x) and \cos(x).

Example 2: Chain Rule Derivative Practice Problems

Next, consider “chain rule derivative practice problems.” Many functions in calculus involve one function inside another, so identifying outer and inner parts helps avoid mistakes.

Example Function

Let f(x) = \sin(4x^3).

Step-by-Step Solution:

1. Identify the outer function as \sin(u), where u = 4x^3.
2. Differentiate the outer function: \frac{d}{du}[\sin(u)] = \cos(u).
3. Differentiate the inner function: \frac{d}{dx}[4x^3] = 12x^2.
4. Apply the chain rule: \frac{d}{dx}[\sin(4x^3)] = \cos(4x^3) \cdot 12x^2.
5. Final expression: 12x^2 \cos(4x^3).

Real-World Connection:

Functions like \sin(4x^3) often appear in engineering scenarios, where a trigonometric expression depends on a polynomial. Therefore, mastering these “chain rule derivative practice problems” ensures smooth progress in advanced fields.

Quick Reference Chart: Important Vocabulary

The following chart highlights essential terms encountered in derivative practice problems:

Term	Definition/Description
Power Rule	\frac{d}{dx}[x^n] = n \cdot x^{n-1}. Used for polynomials.
Product Rule	(f \cdot g)' = f' \cdot g + f \cdot g'. Helpful for multiplying functions.
Chain Rule	(f(g(x))' = f'(g(x)) \cdot g'(x). Necessary for composite functions.
Quotient Rule	\big(\frac{f}{g}\big)'=\frac{f'g - fg'}{g^2}. Used for dividing functions.

Conclusion

These “derivative practice problems” demonstrate how to apply the power rule, product rule, chain rule, and quotient rule. Remember, the “derivative of xsinx” showcases a classic product rule example. Meanwhile, “chain rule derivative practice problems” appear in many real-world situations, so it is wise to practice them often.

After reviewing these steps, exploring additional examples is a good way to fortify skills. Therefore, try mixing rules—like combining chain and product rules—to deepen understanding. Ongoing practice ensures readiness for AP® Calculus AB and BC exams and beyond.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.