Derivatives serve as a foundation of calculus. They measure how quickly a function changes. However, when dealing with more complex expressions in AP® Calculus AB-BC, it is no longer enough to memorize simple differentiation rules. The concept of multiplying functions, covered in 2.8 the product rule, introduces a critical tool for success: the derivative product rule.
Understanding the product rule calculus is vital because many real-world and test-related problems involve products of functions. These might include polynomials multiplied by exponential functions, trigonometric functions multiplied by logarithms, or other combinations. Mastering the derivative product rule prepares students for advanced topics and ensures a strong grasp of calculus fundamentals.
What We Review
What Is the Product Rule?
The derivative product rule is a method to find the derivative of two functions multiplied together. Suppose there are two functions f(x) and g(x). Instead of the simple approach \frac{d}{dx}\bigl(f(x)g(x)\bigr)=f'(x)g'(x) (which is incorrect!), the correct product rule calculus formula states:
\frac{d}{dx}\bigl(f(x)\cdot g(x)\bigr) = f'(x)\cdot g(x) + f(x)\cdot g'(x)This formula is necessary because differentiating a product of functions demands accounting for how each function changes separately, as well as how they both change together. Without the product rule, it would be impossible to accurately capture all parts of this change.
Detailed Examination of the Product Rule Formula
When applying the derivative product rule, start by labeling components:
- Let u = f(x) and v = g(x)
- Their derivatives are u' = f'(x) and v' = g'(x)
The derivative product rule then becomes:
\frac{d}{dx}(u\cdot v) = u'\cdot v + u \cdot v'It is essential to express all parts clearly in AP® Calculus AB-BC work. Maintaining neat notation helps prevent mix-ups between u, u', v, and v'. This rule applies to many scenarios, including products of polynomials, exponentials, logarithms, or trigonometric functions.
Example 1: Simple Polynomial Case
When first learning 2.8 the product rule, a standard starting point involves multiplying two polynomials.
Problem Statement:
Find the derivative of f(x) = (3x^2 + 2x)(x^3 - 4).
Step-by-Step Solution:
- Let u = 3x^2 + 2x. Then u' = 6x + 2.
- Let v = x^3 - 4. Then v' = 3x^2.
- Apply the product rule: \frac{d}{dx}\bigl(u \cdot v\bigr) = u' \cdot v + u \cdot v'.
- Substitute the expressions: \frac{d}{dx}\bigl((3x^2 + 2x)(x^3 - 4)\bigr) = (6x + 2)(x^3 - 4) + (3x^2 + 2x)(3x^2).
- Simplify each term:
- First part: (6x + 2)(x^3 - 4) = 6x \cdot x^3 + 2 \cdot x^3 - 24x - 8 = 6x^4 + 2x^3 - 24x - 8.
- Second part: (3x^2 + 2x)(3x^2) = 9x^4 + 6x^3.
- Combine like terms: 6x^4 + 2x^3 - 24x - 8 + 9x^4 + 6x^3 = (6x^4 + 9x^4) + (2x^3 + 6x^3) - 24x - 8 = 15x^4 + 8x^3 - 24x - 8.
Therefore, the derivative is 15x^4 + 8x^3 - 24x - 8.
The image below helps demonstrate the product rule in action for the functions u = 3x^2 + 2x and v = x^3 - 4.
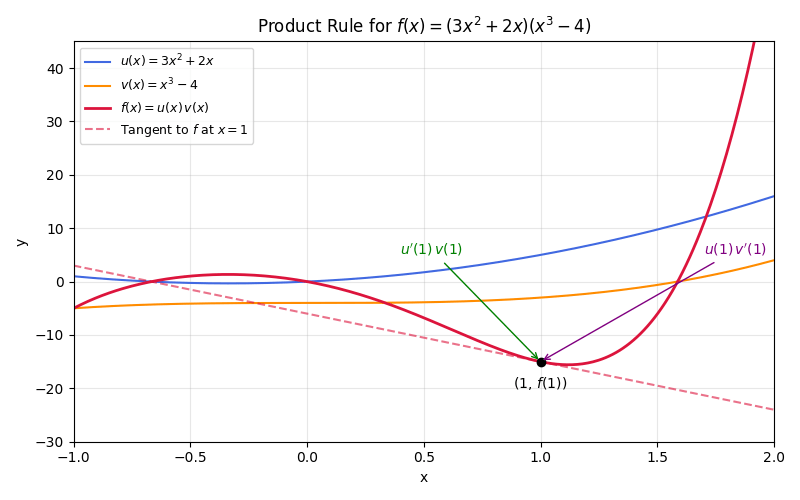
Example 2: Polynomial and Exponential Function
Products frequently combine different function types, such as a polynomial and an exponential. This example highlights the importance of keeping each part in order.
Problem Statement:
Differentiate h(x) = (4x^3 - x + 5)e^{2x}.
Step-by-Step Walkthrough:
- Let u = 4x^3 - x + 5. Then u' = 12x^2 - 1.
- Let v = e^{2x}. To find v', differentiate e^{2x} using the chain rule: \frac{d}{dx}(e^{2x}) = 2e^{2x}. So v' = 2e^{2x}.
- Apply the derivative product rule: \frac{d}{dx}\bigl(u \cdot v\bigr) = u' \cdot v + u \cdot v'.
- Substitute and simplify: \frac{d}{dx}\bigl((4x^3 - x + 5)e^{2x}\bigr) = (12x^2 - 1)e^{2x} + (4x^3 - x + 5)(2e^{2x}).
- Factor out the common e^{2x}: = e^{2x}(12x^2 - 1) + 2e^{2x}(4x^3 - x + 5) = e^{2x}\left[(12x^2 - 1) + 2(4x^3 - x + 5)\right] = e^{2x}\bigl[12x^2 - 1 + 8x^3 - 2x + 10\bigr].
- Combine like terms inside the brackets: = e^{2x}\bigl[8x^3 + 12x^2 - 2x + 9\bigr].
Hence, the derivative is e^{2x}\bigl(8x^3 + 12x^2 - 2x + 9\bigr).
Practical Tips and Common Traps
- Watch for sign errors. A simple minus sign can lead to a wrong final answer.
- Keep steps neat to avoid mixing u' and v'.
- Always double-check by expanding and simplifying carefully.
- Consider verifying results with a quick mental check. For instance, if e^{2x} is in the original function, it should also appear in the derivative.
VII. Quick Reference Chart
| Term | Definition |
| Differentiable | A function is differentiable if its derivative exists. |
| Product Rule | \frac{d}{dx}(uv) = u'v + uv', used when finding the derivative of two multiplied functions. |
| Derivative | Measures the rate of change of a function with respect to its input. |
| Sign Errors | Mistakes that occur when positive or negative signs are dropped or misplaced. |
| Polynomial | A function consisting of sums of terms like ax^n. |
These notes reinforce the basic definitions and remind students about key terminology.
Conclusion
The derivative product rule is a powerful technique in 2.8 the product rule and beyond. It ensures that every factor’s rate of change is accounted for when multiplying functions together. By identifying u, u', v, and v', students can use the product rule calculus approach to find derivatives for numerous scenarios.
A steady habit of organizing work, double-checking sign usage, and practicing with different function types helps build mastery. Consistent application of the product rule in AP® Calculus AB-BC practice sessions not only strengthens problem-solving skills but also lays the groundwork for more advanced calculus concepts.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








