The Extreme Value Theorem plays a crucial role in AP® Calculus AB-BC. It guarantees that certain functions have both a highest and lowest point on a given interval. Therefore, it appears often in real-world scenarios involving optimization, such as locating the maximum profit or the minimum cost. This post explores “what is the extreme value theorem,” details the “extreme value theorem conditions,” and demonstrates how to apply it in practical examples.
What We Review
What Is the Extreme Value Theorem?
The Extreme Value Theorem states that if a function f(x) is continuous on a closed interval [a, b], then f(x) must have both a maximum and a minimum value somewhere in that interval. In simpler words, if there are no gaps or jumps in the function, and the interval includes the boundary points, then the function is guaranteed to have a highest point and a lowest point. These “extreme value theorem conditions” (namely, continuity and having a closed interval) are crucial for applying the theorem.
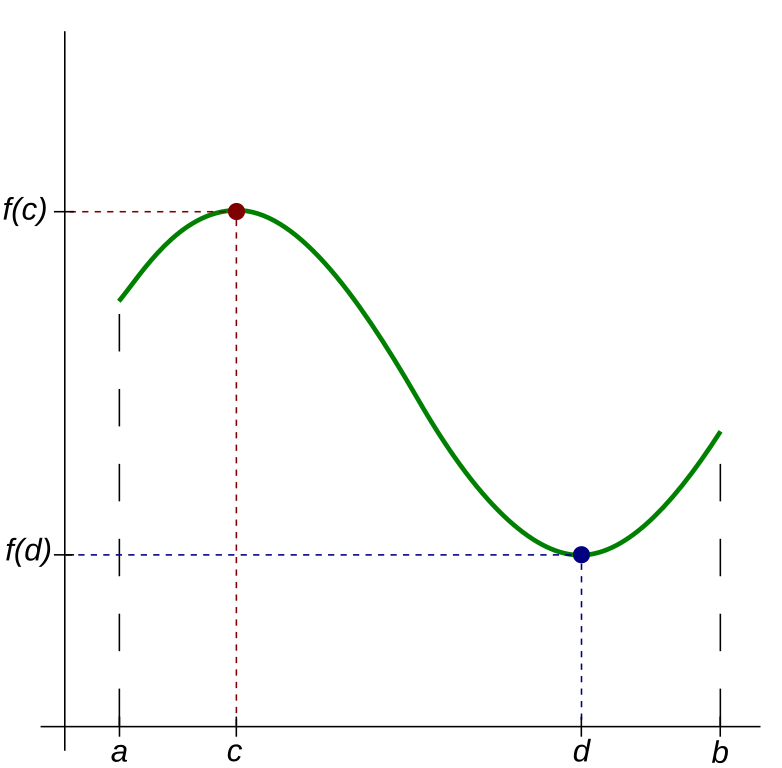
Why the Extreme Value Theorem Matters
Many real-world problems depend on finding the largest or smallest possible value of certain quantities. For instance, a business might want to know when profit peaks or how to reduce costs to the lowest level. Therefore, the theorem offers a guarantee that these extreme values exist, provided the function meets the conditions. Furthermore, this reassurance helps narrow down search areas for optimization, making calculations more efficient.
Step-by-Step Example 1
Consider the continuous function f(x) = x^2 - 4x + 3 on the closed interval [0, 5]. This example will show how to use the extreme value theorem conditions to confirm the existence of a highest and lowest value.
- Check continuity:
- The function f(x) = x^2 - 4x + 3 is a polynomial, so it is continuous for all real x. Hence, it is continuous on [0,5].
- Identify critical points:
- Find the derivative: f'(x) = 2x - 4.
- Set the derivative equal to zero: 2x - 4 = 0, which gives x = 2.
- The value x=2 is the only critical point within the interval.
- Evaluate the function at the critical point and endpoints:
- Check the left endpoint: f(0) = 0^2 - 4(0) + 3 = 3.
- Check the critical point: f(2) = 2^2 - 4(2) + 3 = 4 - 8 + 3 = -1.
- Check the right endpoint: f(5) = 5^2 - 4(5) + 3 = 25 - 20 + 3 = 8.
- Determine the extrema:
- The minimum value is -1 at x=2.
- The maximum value on [0,5] is 8 at x=5.
Therefore, the function has a minimum and maximum on the interval, which aligns with the extreme value theorem.
Additional Example 2
Now consider a different function g(x) = \sin(x) + 2 on the closed interval \left[\frac{\pi}{2}, \frac{5\pi}{2}\right]. This example helps illustrate the same process on a trigonometric function.
- Check continuity:
- The function \sin(x) + 2 is continuous for all real x. Therefore, it meets the continuity requirement on \left[\frac{\pi}{2}, \frac{5\pi}{2}\right].
- Identify critical points:
- The derivative is g'(x) = \cos(x).
- Set it equal to zero: \cos(x) = 0.
- On \left[\frac{\pi}{2}, \frac{5\pi}{2}\right], the solutions to \cos(x)=0 are x = \frac{\pi}{2}, \frac{3\pi}{2}, and \frac{5\pi}{2}. However, note that \frac{\pi}{2} and \frac{5\pi}{2} are endpoints, but they also satisfy the derivative condition.
- Evaluate the function at the critical point and endpoints:
- Left endpoint: g\left(\frac{\pi}{2}\right) = \sin\left(\frac{\pi}{2}\right) + 2 = 1 + 2 = 3.
- Critical point in the interior: x = \frac{3\pi}{2}, so g\left(\frac{3\pi}{2}\right) = \sin\left(\frac{3\pi}{2}\right) + 2 = -1 + 2 = 1.
- Right endpoint: g\left(\frac{5\pi}{2}\right) = \sin\left(\frac{5\pi}{2}\right) + 2 = 1 + 2 = 3.
- Determine the extrema:
- The minimum is 1 at x = \frac{3\pi}{2}.
- The maximum, which equals 3, occurs at both endpoints x=\frac{\pi}{2} and x=\frac{5\pi}{2}.
Hence, the continuity and closed interval properties allow us to confirm a maximum and a minimum, as the extreme value theorem states.
Common Mistakes and Pitfalls
Many students forget to check the function at the endpoints of the interval, focusing only on critical points. However, endpoints often contain the actual maximum or minimum for a closed interval. Another pitfall occurs when the function is not continuous. Discontinuities or undefined points mean the extreme value theorem conditions are not met, and it might be impossible to guarantee a highest or lowest point.
Quick Reference Chart
Below is a quick guide to essential terms related to the Extreme Value Theorem:
| Term | Definition |
| Continuous Function | A function with no breaks, holes, or jumps on an interval. |
| Closed Interval | An interval [a, b] that includes both endpoints a and b. |
| Absolute Maximum | The highest function value on the interval. |
| Absolute Minimum | The lowest function value on the interval. |
| Critical Points | Points where the derivative is zero or undefined, potentially indicating local extrema. |
Conclusion
The Extreme Value Theorem is essential for finding the highest and lowest values of a continuous function, as long as the function is defined on a closed interval. Therefore, always confirm the “extreme value theorem conditions” by checking that the function is continuous and that the interval is not open-ended. Properly identifying critical points and endpoints ensures no extreme values are missed. Finally, deeper knowledge of limits and derivatives can enhance understanding of why the theorem holds, preparing students for more advanced calculus topics.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 5.1 Using the Mean Value Theorem
- 5.3 Determining Intervals on Which a Function Is Increasing or Decreasing
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








