What We Review
Introduction
Sine and cosine functions are essential building blocks in trigonometry and precalculus. They help model various real-life phenomena, such as sound waves and tides. Understanding graphing a transformation of sine and cosine is key to mastering these functions in AP® Precalculus. Transformations change how functions look on a graph, affecting their position and shape. Therefore, learning about these shifts and stretches will make it easier to analyze and interpret sinusoidal graphs.
Key Concepts in Transformations of Sine and Cosine
Sinusoidal Functions: Sinusoidal functions are a family of functions that include sine and cosine. They have a wave-like shape and can be transformed in several ways.
- Structure of Sinusoidal Functions:
- f(\theta) = a \sin(b(\theta + c)) + d
- g(\theta) = a \cos(b(\theta + c)) + d
The parameters (a), (b), (c), and (d) control the graph’s amplitude, period, phase shift, and vertical shift, respectively.
Understanding Vertical and Horizontal Transformations
Vertical Transformations:
- Amplitude: This is how “tall” the waves are. It is the distance from the middle (midline) of the wave to the peak. The value of (a) tells us the amplitude of the sinusoidal function.
- Vertical Shift: This moves the entire graph up or down. This shift is represented by (d).
Example: Graph the functions:
- (g(\theta) = 2\sin(\theta))
- (h(\theta) = \sin(\theta) + 3)
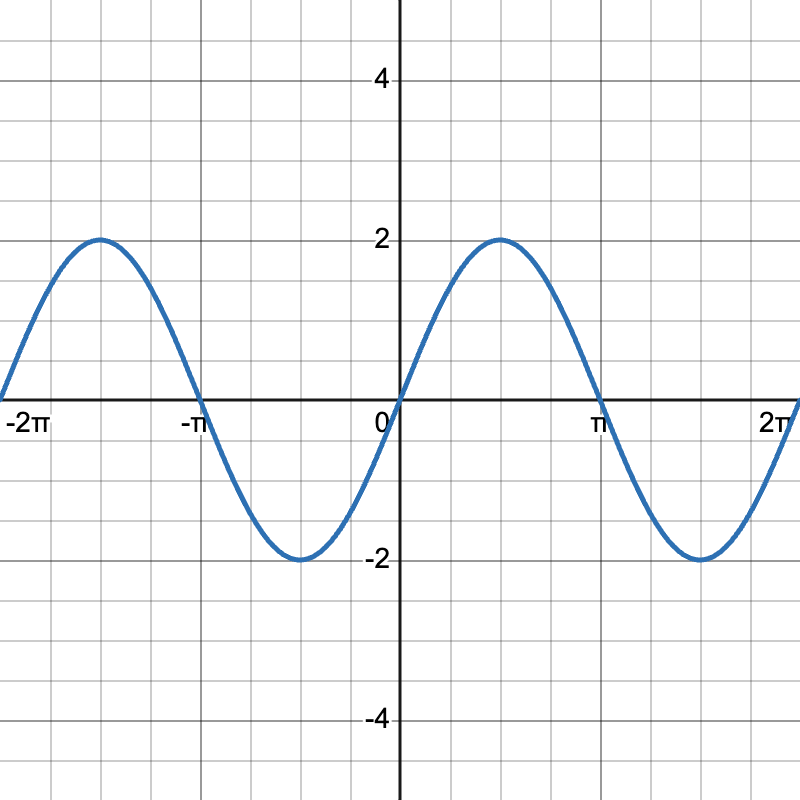
1. For (g(\theta) = 2\sin(\theta)):
- Amplitude: (|2| = 2)
- Vertical Shift: (d = 0) (no vertical shift)
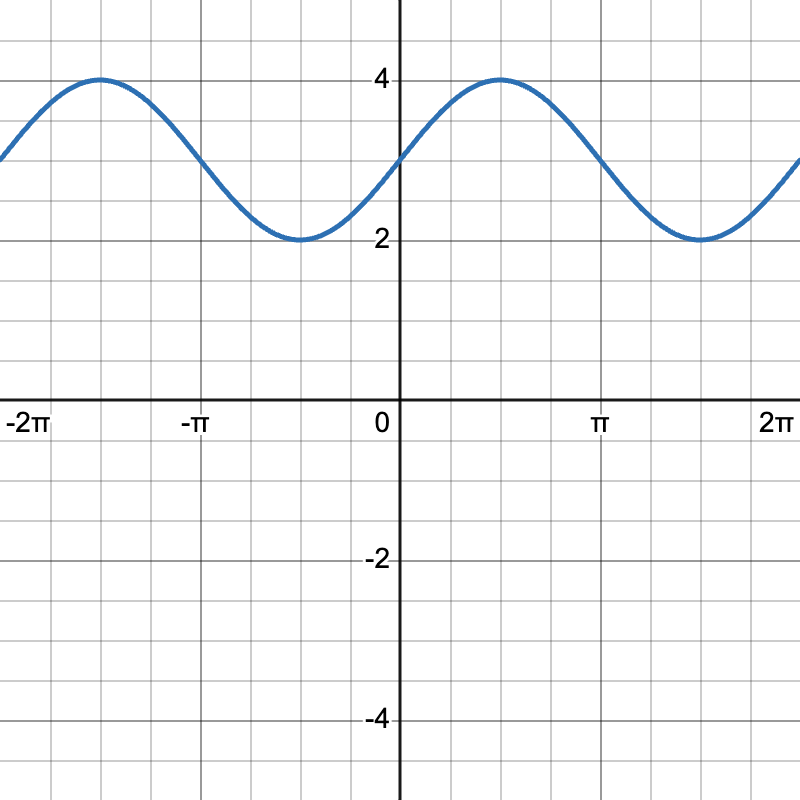
2. For (h(\theta) = \sin(\theta) + 3):
- Amplitude: (|1| = 1)
- Vertical Shift: (d = 3) (shift up by 3)
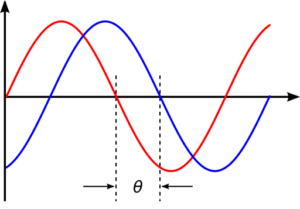
Horizontal Transformations:
- Period: The duration of one complete wave cycle. Affected by (b) in the function.
- Phase Shift: Moves the graph to the left or right, determined by (c).
Example: Analyze the function (j(\theta) = \sin(2(\theta - \frac{\pi}{4})))
- Period: (\frac{2\pi}{|2|} = \pi)
- Phase Shift: Moves (\frac{\pi}{4}) to the right
Amplitude, Period, and Phase Shift
- Amplitude: (|a|), the height of the wave from its center.
- Period: (\frac{2\pi}{|b|}), the length of one wave cycle.
- Phase Shift: (-c), how far the graph shifts horizontally.
Let’s analyze the function (k(\theta) = 3 \cos(0.5(\theta + \pi)) - 1):
- Amplitude: (|3| = 3)
- Period: (\frac{2\pi}{|0.5|} = 4\pi)
- Phase Shift: (-\pi) moves left by (\pi)
- Vertical Shift: Shift down by 1 unit
Graphing reveals these transformations visibly adjust the wave’s look.
Summary of Key Characteristics of Sinusoidal Functions
In summary, sinusoidal functions can be transformed by adjusting amplitude, period, vertical shift, and phase shift:
- Amplitude: Determines wave height.
- Period: Affects the length of one complete cycle.
- Vertical Shift: Moves the graph up or down.
- Phase Shift: Moves the graph left or right.
Grasping these characteristics makes it simpler to graph sinusoidal functions and analyze their real-world applications.
Quick Reference Chart
| Term | Definition |
| Amplitude | The maximum distance from the midline to the peak. |
| Period | The length of one complete cycle of the wave. |
| Vertical Shift | The displacement of the midline from (y = 0). |
| Phase Shift | The horizontal shift of the graph. |
Conclusion
Students are encouraged to practice identifying transformations of sine and cosine functions using these guidelines. Doing so will enhance their ability to understand and master such concepts in AP® Precalculus. Remember, transforming sine and cosine functions is not just a math exercise—it’s a tool for interpreting the world through a mathematical lens.
Sharpen Your Skills for AP® Precalculus
Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 3.4 Sine and Cosine Function Graphs
- 3.5 Sinusoidal Functions
- 3.7 Sinusoidal Function Context and Data Modeling
Need help preparing for your AP® Precalculus exam?
Albert has hundreds of AP® Precalculus practice questions, free responses, and an AP® Precalculus practice test to try out.









