Integrating a vector is a key concept in AP® Calculus AB-BC because it extends the idea of single-variable integration to multi-component functions. In many real-world applications, objects move through space with both horizontal and vertical changes. Therefore, understanding vector integration helps describe the position of moving objects more accurately.

Moreover, this process is closely related to real-valued integration, since each component of a vector valued function can be integrated just like a single-variable function. Consequently, revisiting basic integration rules before studying this topic is recommended. The goal of this review is to provide a clear outline of how to integrate a vector, step by step.

Understanding Vector-Valued Functions

A vector valued function is a function where the output is a vector. In other words, each input t corresponds to a vector of components. For a 2D function, one might write:

\vec{r}(t) = \langle x(t), y(t) \rangle

Similarly, a 3D function may include a third component z(t):

\vec{r}(t) = \langle x(t), y(t), z(t) \rangle

Next, recall that parametric equations from earlier lessons link the parameter t to separate x(t) and y(t) equations. In a vector context, each component is treated similarly, but they are grouped together to represent a full motion in space.

Indefinite Integrals of Vector-Valued Functions

When performing vector integration, each component is integrated individually. Thus, for a vector valued function:

\vec{r}(t) = \langle x(t), y(t) \rangle

The indefinite integral is:

\int \vec{r}(t) dt = \langle \int x(t) dt, \int y(t) dt \rangle + \vec{C}

Notice that the constant of integration for a 2D or 3D function is itself a vector. Therefore, each component could have its own constant.

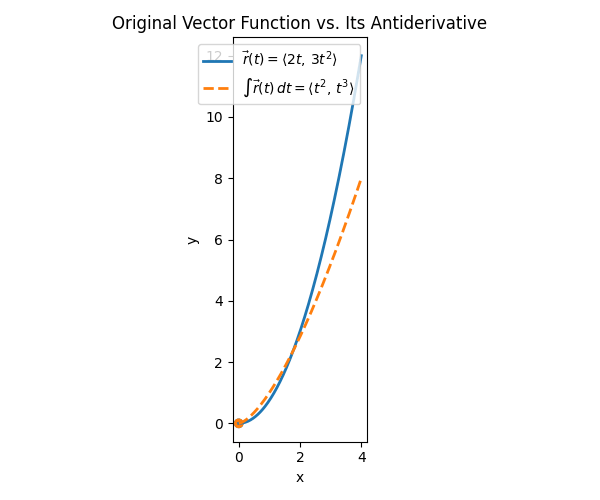
Example 1: 2D Vector Function

Suppose a vector valued function is given by:

\vec{r}(t) = \langle 2t, 3t^2 \rangle

Find its indefinite integral.

• Step 1: Separate each component.
  • The x-component is 2t.
  • The y-component is 3t^2.

• Step 2: Integrate each component.
  • \int 2t dt = t^2 + C_1
  • \int 3t^2 dt = t^3 + C_2

• Step 3: Combine to form the vector.
  • \int \vec{r}(t) dt = \langle t^2 + C_1, t^3 + C_2 \rangle

Therefore, the indefinite integral is \langle t^2 + C_1, t^3 + C_2 \rangle, where C_1 and C_2 are constants.

Practice Problem (Indefinite Integral)

Find the indefinite integral of:

\vec{F}(t) = \langle 4t^3, 5 \rangle

Step-by-Step Solution:

1. Integrate the x-component: \int 4t^3 dt = t^4 + K_1
2. Integrate the y-component: \int 5 dt = 5t + K_2
3. Combine to form the general solution: \int \vec{F}(t) dt = \langle t^4 + K_1, 5t + K_2\rangle

Definite Integrals of Vector-Valued Functions

A definite integral of a vector valued function from t=a to t=b is calculated by integrating each component over the interval and then evaluating at the bounds. Thus, for:

\vec{r}(t) = \langle x(t), y(t), z(t) \rangle

The definite integral is:

\int_{a}^{b} \vec{r}(t) dt = \langle \int_{a}^{b} x(t) dt, \int_{a}^{b} y(t) dt, \int_{a}^{b} z(t) dt \rangle

Example 2: 3D Vector Function

Consider a vector valued function:

\vec{v}(t) = \langle 2t, t^2, 1 \rangle

Evaluate \int_{0}^{2} \vec{v}(t)dt.

Step 1: Integrate each component from 0 to 2.

• \int_{0}^{2} 2t dt = [t^2]_{0}^{2} = (2^2) - (0^2) = 4
• \int_{0}^{2} t^2 dt = [\frac{t^3}{3}]_{0}^{2} = \frac{2^3}{3} - 0 = \frac{8}{3}
• \int_{0}^{2} 1 dt = [t]_{0}^{2} = 2 - 0 = 2

Step 2: Combine the results into a vector.

• \int_{0}^{2} \vec{v}(t) dt = \langle 4, \frac{8}{3}, 2\rangle

Hence, the definite integral equals \langle 4, \frac{8}{3}, 2\rangle.

Practice Problem (Definite Integral)

Evaluate \int_{1}^{3} \langle 6, 2t, t-1 \rangle dt.

Step-by-Step Solution:

1. Integrate each component over [1, 3].
   • \int_{1}^{3} 6 dt = [6t]_{1}^{3} = 6(3) - 6(1) = 12
   • \int_{1}^{3} 2t dt = [t^2]_{1}^{3} = 3^2 - 1^2 = 9 - 1 = 8
   • \int_{1}^{3} (t - 1) dt = [\frac{t^2}{2} - t]_{1}^{3} = \left(\frac{3^2}{2} - 3\right) - \left(\frac{1^2}{2} - 1\right) = \left(\frac{9}{2} - 3\right) - \left(\frac{1}{2} - 1\right) = \left(\frac{9}{2} - \frac{6}{2}\right) - \left(\frac{1}{2} - \frac{2}{2}\right) = \frac{3}{2} - \left(-\frac{1}{2}\right) = 2
2. Combine the evaluated components:
   • \int_{1}^{3} \langle 6, 2t, t-1 \rangle dt = \langle 12, 8, 2 \rangle

Common Pitfalls and Helpful Tips

• Always remember to include a separate constant of integration for each component in an indefinite integral. Otherwise, answers may be incomplete.
• When initial conditions are given (for instance, an initial velocity), use those conditions to solve for the constants.
• Confirm the correctness of a vector integral by taking its derivative and checking that it matches the original function. This consistency check is especially helpful in more complex problems.

Quick Reference Chart (Vocabulary and Definitions)

Term	Definition
Vector Valued Function	A function whose output is a vector; typically expressed in components as <x(t), y(t), z(t)>.
Integrating a Vector	The process of finding the antiderivative of each component of a vector-valued function.
Vector Integration	Another term for integrating each component of a vector-valued function.
Indefinite Integral	The general antiderivative of a function, including a constant of integration.
Definite Integral	The evaluation of an integral over a specific interval, producing a numerical result.

Conclusion

In summary, integrating a vector involves treating each component like a single-variable integral. Moreover, it is crucial to include all constants of integration for indefinite integrals. Checking results by differentiating the answer can prevent careless errors.

Ultimately, practicing different types of vector valued functions will build greater intuition about vector integration. By consistently reviewing these steps, students can gain confidence in solving a variety of AP® Calculus AB-BC problems.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.