Integration by partial fractions is a method used in AP® Calculus AB-BC to handle integrals of complex rational functions. It splits a fraction into simpler parts that are easier to integrate. Mastering this skill ensures smoother progress through advanced integration problems, especially when dealing with sums and differences of simpler functions.
This article focuses on the core ideas, shows how to perform the steps, and provides examples with solutions. By the end, it will feel more natural to work with each part of a rational function separately, especially when applying integration by partial fractions. Moreover, it will reinforce skills like factoring and solving for unknown constants.
What We Review
Overview of Integration by Partial Fractions
A rational function is any function that can be written as one polynomial divided by another polynomial, for instance \frac{x^2 + 3}{x - 1}. When the denominator is complicated, integrating directly can be difficult. Therefore, partial fraction decomposition helps split the fraction into simpler terms.
The method often involves “equating coefficients partial fractions.” That phrase means comparing coefficients on both sides of an equation after expressing the original fraction as a sum of simpler fractions. This makes solving for unknown constants straightforward. After that, integrating each smaller fraction is much easier than trying to tackle the original fraction as a whole.
Basic Principles of Partial Fraction Decomposition
Performing partial fraction decomposition can be organized into three key steps:
- Factor the denominator completely, into linear factors (e.g., (x + a)) or irreducible quadratic factors (e.g., (x^2 + bx + c) if it cannot be factored further).
- Express the original function as a sum of simpler fractions. Each distinct linear factor contributes a term like \frac{A}{(x+a)}, while repeated factors or irreducible quadratics introduce slightly different forms.
- Use “equating coefficients” to solve for the unknown constants in these simpler fractions. Rearrange the resulting algebraic equation to match coefficients on both sides.
It may help to verify answers with a partial fraction decomposition calculator with steps. However, ensure each step is performed correctly. Always check any factoring and be mindful of negative signs.
Step-by-Step Example 1
Consider the integral \int \frac{3x + 4}{(x + 2)(x - 1)} dx. Notice that the denominator has two distinct linear factors.
- Factor the denominator (already done): (x + 2)(x - 1).
- Express partial fractions: \frac{3x + 4}{(x + 2)(x - 1)} = \frac{A}{(x + 2)} + \frac{B}{(x - 1)}.
- Combine the right-hand side: \frac{A(x - 1) + B(x + 2)}{(x + 2)(x - 1)}. This must equal \frac{3x + 4}{(x + 2)(x - 1)}.
- “Equating coefficients partial fractions” gives: A(x - 1) + B(x + 2) = 3x + 4.
- Expand: Ax - A + Bx + 2B = 3x + 4.
- Combine like terms: (A + B)x + (-A + 2B) = 3x + 4.
- Therefore:
- A + B = 3
- -A + 2B = 4
- Solve for A and B. From the first equation, A = 3 - B. Put that into the second: -(3 - B) + 2B = 4 \rightarrow-3 + B + 2B = 4 \rightarrow3B = 7\rightarrowB = \frac{7}{3}
- Then A = 3 - \frac{7}{3} = \frac{9 - 7}{3} = \frac{2}{3}
- Notice how the left side and the two terms on the right side graphed together show the same asymptotes.
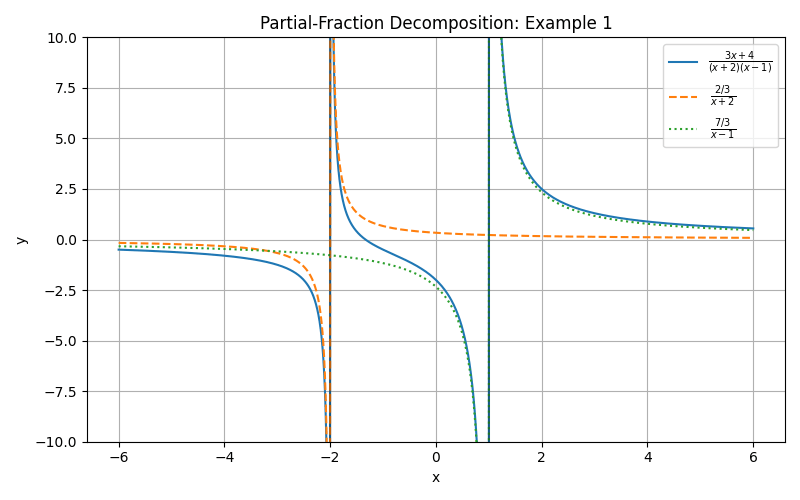
5. Rewrite the integrand: \frac{3x + 4}{(x + 2)(x - 1)} = \frac{\frac{2}{3}}{(x + 2)} + \frac{\frac{7}{3}}{(x - 1)}.
6. Integrate term by term: \int \left(\frac{\frac{2}{3}}{(x + 2)} + \frac{\frac{7}{3}}{(x - 1)}\right) dx= \frac{2}{3} \int \frac{1}{(x + 2)} dx + \frac{7}{3} \int \frac{1}{(x - 1)} dx= \frac{2}{3} \ln|x + 2| + \frac{7}{3} \ln|x - 1| + C.
Hence, the final answer is \frac{2}{3} \ln|x + 2| + \frac{7}{3} \ln|x - 1| + C.
Step-by-Step Example 2
Now, look at an integral with repeated factors: \int \frac{2x^2 + 3x + 1}{(x + 1)^2 (x - 2)} dx. This setup shows how repeated linear factors influence the decomposition.
- Factor the denominator (already factored): (x + 1)^2 (x - 2).
- Set up partial fractions: \frac{2x^2 + 3x + 1}{(x + 1)^2 (x - 2)} = \frac{A}{(x + 1)} + \frac{B}{(x + 1)^2} + \frac{C}{(x - 2)}.
- Combine everything into a single fraction. The numerator on the right-hand side becomes: A(x + 1)(x - 2) + B(x - 2) + C(x + 1)^2 .
- Expand and “equate coefficients partial fractions.” Then solve for A, B, and C.
- First, expand each term:
- A(x+1)(x-2) = A(x^2 - x - 2).
- B(x-2) = Bx - 2B.
- C(x+1)^2 = C(x^2 + 2x + 1).
- Summing those gives: A x^2 - A x - 2A + Bx - 2B + Cx^2 + 2Cx + C.
- Group like terms: (A + C)x^2 + (-A + B + 2C)x + (-2A - 2B + C).
- That must match 2x^2 + 3x + 1. So:
- A + C = 2
- -A + B + 2C = 3
- -2A - 2B + C = 1
- Solve these equations carefully to find A, B, and C.
- First, expand each term:
- Rewrite the original fraction with the found constants, then integrate each partial fraction: \int \left( \frac{A}{(x + 1)} + \frac{B}{(x + 1)^2} + \frac{C}{(x - 2)} \right) dx.
- The general antiderivatives are:
- \int \frac{A}{(x+1)} dx = A \ln|x+1|
- \int \frac{B}{(x+1)^2} dx = \frac{-B}{x+1} (since \frac{d}{dx}\left(\frac{-1}{x+1}\right) = \frac{1}{(x+1)^2}
- \int \frac{C}{(x-2)} dx = C \ln|x-2|
- The general antiderivatives are:
Combine these results plus the constant of integration to get the final answer.
Tips and Common Pitfalls
- Always factor the denominator completely before starting.
- Be very meticulous when recombining the fractions or “equating coefficients partial fractions.” Small mistakes with signs can lead to incorrect constants.
- Double-check your work by adding the fractions back together to see if the original function reappears.
- Watch out for constants during integration. Missing the constant of integration is a common error.
- Consider using a partial fraction decomposition calculator with steps, but be sure to understand each step rather than just relying on the outcome.
Quick Reference Chart of Key Vocabulary
| Term/Expression | Definition/Key Feature |
| Integration by Partial Fractions | A technique for integrating complex rational functions by splitting into simpler parts. |
| Rational Function | A function defined by one polynomial divided by another (e.g., \frac{x^2 + 1}{x - 3}). |
Conclusion
Integration by partial fractions is an essential skill in AP® Calculus AB-BC because it transforms tough integrals into manageable ones. It applies factoring, algebraic manipulation, and basic integration rules. Therefore, practicing on various forms, including repeated factors and irreducible quadratics, is recommended. This strategy will lead to stronger problem-solving abilities and better understanding of more advanced calculus problems.
Keep revisiting these techniques and apply them to different examples. The confidence gained will extend to other integration methods and help tie together multiple concepts across the AP® Calculus curriculum.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








