The lagrange error bound formula helps predict how far a Taylor polynomial might be from the true value of a function. Therefore, it is a crucial tool when using Taylor polynomial approximations. It tells us the maximum possible error, also known as the remainder, after approximating a function.
In AP® Calculus AB-BC, students often encounter these ideas in free-response and multiple-choice questions. Indeed, knowing how to do lagrange error bound calculations or use the lagrange error formula appropriately can save time and assure higher accuracy on exams. This concept helps evaluators see if an approximation is precise enough and also indicates where additional terms might be necessary.
What We Review
Quick Refresher on Taylor Polynomials
Recap of Taylor Polynomial Concepts
A Taylor polynomial is a sum of terms derived from a function’s derivatives, all evaluated at a specific center point (for example, x = 0). These polynomials are built to approximate the function near that center. Consequently, they become a powerful way to find approximate values without relying on a calculator for every calculation.
Short Example with Steps
Consider the function f(x) = e^x. To create a Taylor polynomial of degree 2 around x = 0:
- Find the first few derivatives of e^x.
- f(x) = e^x
- f'(x) = e^x
- f''(x) = e^x
- Evaluate these derivatives at x = 0:
- f(0) = 1, f'(0) = 1, f''(0) = 1.
- Plug these values into the Taylor polynomial formula for degree 2:
- p_2(x) = 1 + x + \frac{x^2}{2!}.
This polynomial approximates e^x near x = 0. However, to know how good this approximation is, an error bound is needed.
Understanding the Lagrange Error Bound Formula
Definition and Formula
The lagrange error bound formula provides an upper bound on how large the error can be when using a Taylor polynomial of degree n. It is commonly written as: \displaystyle \left| R_n(x) \right| \le \frac{M}{(n+1)!}\left| x-a \right|^{n+1} …where:
- R_n(x) is the remainder (or error) after using the n-th degree polynomial.
- M is the maximum of the absolute value of the n+1-th derivative on the interval.
- a is the center of the expansion.
Conceptual Explanation
This bound shows the largest possible difference between the Taylor polynomial and the true function. Therefore, the key to applying the lagrange error formula is correctly determining M. Often, M is found by analyzing the n+1-th derivative over the interval used.
Step-by-Step Example: Lagrange Error Bound Formula
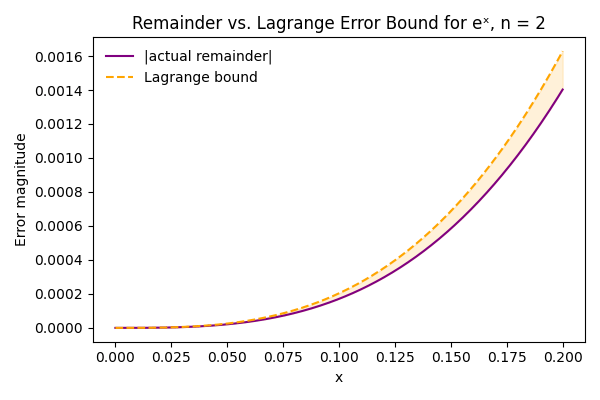
Use f(x) = e^x and the degree 2 polynomial p_2(x) from earlier, centered at x=0. Suppose we want to approximate e^{0.2}. The next steps use the lagrange error bound formula:
- Identify the n+1-th derivative. Since our polynomial degree n = 2, the 3-rd derivative is f^{(3)}(x) = e^x.
- Find M. On 0 \le x \le 0.2, the maximum of e^x is at x=0.2. Thus, M = e^{0.2}.
- Compute the error bound using \displaystyle \frac{M}{(n+1)!}\left| x - 0\right|^{n+1}: \displaystyle \left| R_2(0.2) \right| \le \frac{e^{0.2}}{3!}(0.2)^{3}.
- Simplify. Note that 3! = 6 and e^{0.2} is just a positive constant.
Hence, the maximum error is \displaystyle \frac{e^{0.2}(0.2)^{3}}{6}. That means the true value of e^{0.2} will be within that range above or below the polynomial’s value.
The Alternating Series Error Bound (Comparison)
When the Alternating Series Error Bound Applies
Sometimes, a series has terms that alternate in sign, such as (-1)^n or (-1)^{n+1}. In those cases, the alternating series error bound applies. Alternatively, the lagrange error bound formula might be more useful if the series is not strictly alternating.
Example Problem Demonstration
Consider the Maclaurin series for \cos x: \displaystyle \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots.
- Suppose we keep only two terms: 1 - \frac{x^2}{2}.
- Because this is an alternating series, the alternating series error bound states that the error is at most the absolute value of the first neglected term, which is \frac{|x|^4}{4!} for this scenario.
- If x=0.1, the error is at most \frac{(0.1)^4}{4!}, which can be calculated quickly.
Thus, for many alternating series, this approach can be a faster alternative than learning how to do lagrange error bound calculations, provided the strict alternating conditions are met.
Practical Tips for Evaluating Error Bounds
Choosing the Right Method
Deciding to use the lagrange error formula or an alternating series error bound depends on the series. If terms alternate consistently, the alternating error bound is quick. However, if terms do not alternate, the lagrange error bound formula is the go-to strategy.
Common Pitfalls
Many learners incorrectly identify M. Always verify the maximum value of the derivative on the appropriate interval. Another common mistake is mixing up which derivative to use. Remember: if you use an n-th degree polynomial, you need the n+1-th derivative for the error calculation.
Example Applications in AP® Calculus
Typical Exam-Style Questions
During the exam, you might be asked to find the remainder term or the maximum possible error for a Taylor polynomial approximation. Often, the problem will specify an interval and ask for an appropriate value of M. Alternatively, the question may request an alternating series estimate if the function is known to alternate in sign.
Strategies for Success
Always show derivative work when finding M. In addition, clearly state the formula being used. If you are dealing with an alternating series, confirm the signs are strictly alternating. That way, the correct error bound is chosen, and partial credit losses are minimized.
VII. Quick Reference Chart: Important Vocabulary and Definitions
| Term | Definition/Explanation |
| Taylor Polynomial | Polynomial used to approximate a function near a specific point |
| Lagrange Error Bound | Provides an upper limit on the error of a Taylor polynomial approximation |
| Remainder (Error) | The difference between the actual function value and the polynomial value |
| M | The maximum value of the (n+1)-th derivative on the interval of interest |
| Alternating Series Error | An error bound that applies when terms of a series alternate in sign |
Conclusion
The lagrange error bound formula is vital for ensuring Taylor polynomial approximations are trustworthy. Always remember the key steps: identify the n+1-th derivative, evaluate its maximum on the interval, and plug it into the formula. For alternating series, the alternating series error bound can sometimes be a simpler strategy.
Practice helps these techniques feel natural. Therefore, repeatedly solving problems will build confidence and ensure success on both homework and exams.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








