Riemann sums are used to estimate the area under a curve by adding small, rectangular slices. These sums serve as the foundation for integrals. Understanding how the limit of a Riemann sum relates to a definite integral is a key concept in AP® Calculus AB-BC.
Therefore, this post explains how to set up a Riemann sum and then see why it converges to a definite integral. This knowledge is essential for anyone wanting to move from summation notation to definite integral notation.
What We Review
What Is a Riemann Sum?
Defining Subintervals and Partitions
To begin, consider an interval [a, b] on the x-axis. Divide this interval into n smaller sections called subintervals. Each subinterval has a width labeled \Delta x.
Therefore, if the interval [a, b] has length b - a, then:
\Delta x = \frac{b - a}{n}Next, write all subintervals as:
[a, a + \Delta x], [a + \Delta x, a + 2\Delta x], \dots, [a + (n-1)\Delta x, b]Evaluating the Function on Each Subinterval
Within each subinterval, choose a sample point x_i. This point can be at the left end, right end, or somewhere in the middle of the subinterval. Then, calculate the function value f(x_i).
Next, multiply f(x_i) by the width \Delta x. This product represents the area of one rectangle whose height is f(x_i) and base is \Delta x.
Summation
After finding f(x_i) \Delta x for each subinterval, sum all those products. The Riemann sum is:
\sum_{i=1}^{n} f(x_i) \Delta xAs n gets larger, \Delta x gets smaller. Therefore, the total sum becomes more accurate.
Understanding the Limit of a Riemann Sum
Convergence to the Definite Integral
When the number of subintervals increases toward infinity, \Delta x \rightarrow 0. In that limit, the Riemann sum provides the exact area under f(x) from x=a to x=b. This idea is crucial for recognizing that:
\lim_{n \to \infty} \sum_{i=1}^n f(x_i^*) \Delta x = \text{Exact Area}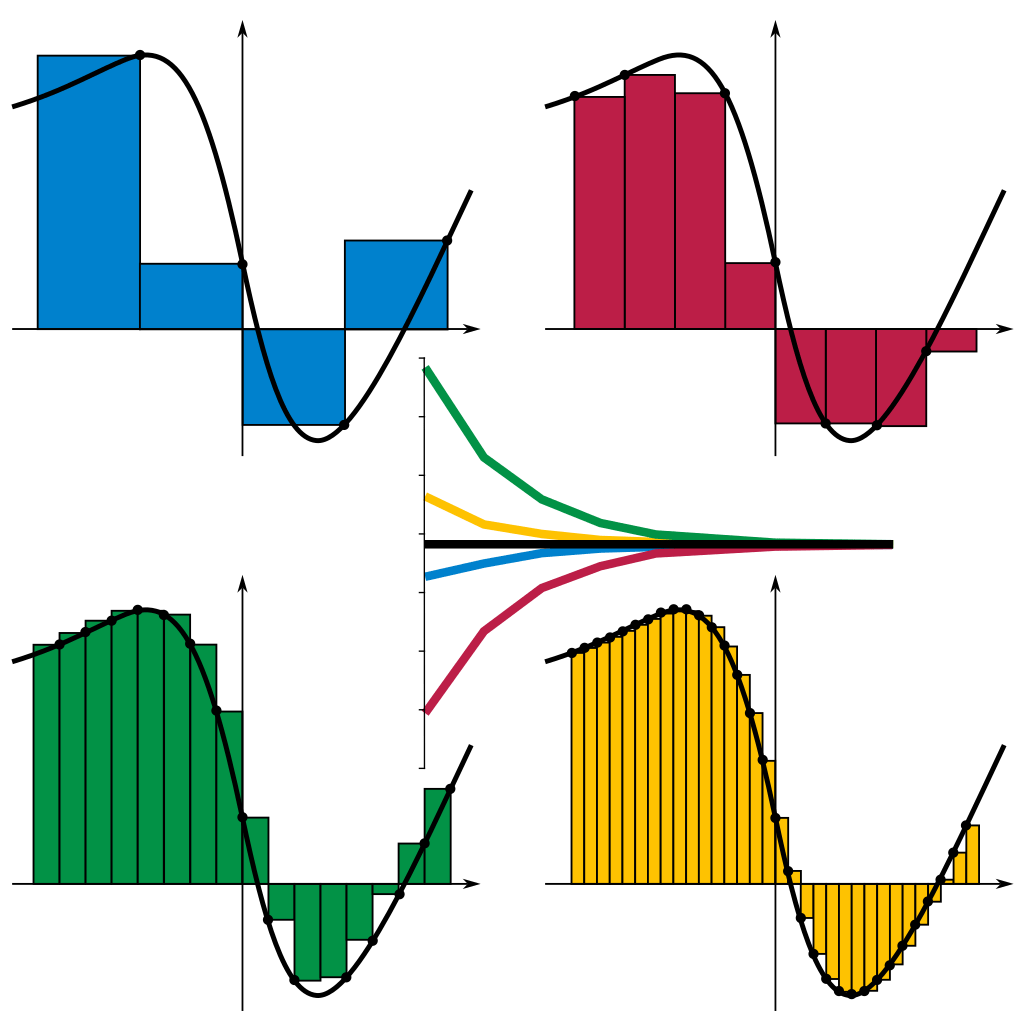
Definite Integral Notation
The definite integral notation connects directly to this limit. It is written as:
\int_{a}^{b} f(x) dxHence, the integral symbol \int can be viewed as a “fancy S,” which stands for summation. The expression \int_{a}^{b} f(x) , dx exactly equals the limit of the Riemann sum.
Converting a Riemann Sum to a Definite Integral
Converting a Riemann sum to a definite integral involves replacing \sum_{i=1}^{n} f(x_i^*) \Delta x with \int_{a}^{b} f(x) , dx in the limit as n \rightarrow \infty.
Therefore, if a problem begins in summation notation, apply the limit process. Then rewrite with the integral sign and the correct bounds. This step is central in AP® Calculus when moving from a Riemann sum to integral notation.
Example: Riemann Sum to Definite Integral
Write a definite integral equivalent to the following limit.
\lim\limits_{n \to \infty} \sum_{i=1}^n \left( \cos\left( \dfrac{2i}{n} \right) \cdot \dfrac{3}{n} \right)
We are given the limit:
\lim\limits_{n \to \infty} \sum_{i=1}^n \left( \cos\left( \dfrac{2i}{n} \right) \cdot \dfrac{3}{n} \right)
This is a Riemann sum of the form:
\lim\limits_{n \to \infty} \sum_{i=1}^n f(x_i^*) \cdot \Delta x
Identify \Delta x
The \Delta x term is the constant multiplier outside the function, which in this case is:
\Delta x = \dfrac{3}{n}
Determine the interval
Since \Delta x = \dfrac{b - a}{n}, and \Delta x = \dfrac{3}{n}, it must be that:
b - a = 3
This means the interval has length 3. If we assume the first subinterval starts at x = 0, then:
a = 0,\quad b = 3
Identify x_i^*
In the sum, we see:
\cos\left( \dfrac{2i}{n} \right)
We want to express this in terms of x_i^* = a + i \cdot \Delta x. From Step 2, we know:
x_i^* = 0 + i \cdot \dfrac{3}{n} = \dfrac{3i}{n}
So we want:
\cos\left( \dfrac{2i}{n} \right) = f(x_i^*) = f\left( \dfrac{3i}{n} \right)
This means the function is:
f(x) = \cos\left( \dfrac{2}{3}x \right)
Write the equivalent definite integral
Now we can rewrite the Riemann sum as a definite integral:
\int_0^3 \cos\left( \dfrac{2}{3}x \right) \, dx
So the final answer is:
\int_0^3 \cos\left( \dfrac{2}{3}x \right) \, dx
Quick Reference Chart (Vocabulary and Definitions)
| Term | Definition/Explanation |
| Riemann Sum | A sum of function values times subinterval widths that approximates the area under a curve. |
| Subinterval | A smaller division of the interval [a, b]. |
| \Delta x | The width of each subinterval. |
| Sample Point (x_i^*) | A point in each subinterval at which the function value is found. |
| Definite Integral | The limit of Riemann sums, representing the exact area under f(x) between x = a and x = b. |
Conclusion
In summary, the limit of a Riemann sum reveals the precise area under f(x). This is exactly what the definite integral represents. Consequently, definite integral notation is a compact way to show the result of adding infinitely many small pieces under a curve.
Finally, converting a Riemann sum to a definite integral is an essential skill for advanced calculus topics. Mastery of this connection between a finite sum and its limit as n \to \infty will pave the way for applying the Fundamental Theorem of Calculus and beyond.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








