Limits at infinity play a crucial role in understanding how functions behave as numbers grow very large in the positive or negative direction. These ideas often appear on the AP® Calculus AB-BC exams, especially in topics connected to 1.15 limits at infinity and horizontal asymptotes. In particular, College Board objectives LIM-2.D.3, LIM-2.D.4, and LIM-2.D.5 highlight how limits at infinity help describe the end behavior of various functions. Therefore, a solid grasp of these concepts allows learners to tackle more advanced problems involving asymptotes, continuity, and convergence in later chapters.
What We Review
What Are Limits at Infinity?
A limit at infinity refers to the value a function approaches as the variable goes toward positive or negative infinity. For instance, if \lim_{x \to \infty} f(x) = L exists, it implies that the function f(x) settles closer and closer to L as x becomes extremely large.
These limits are used to evaluate the end behavior of functions in many contexts. In particular, understanding limits of this type helps predict whether a function approaches a constant value or whether it grows without bound. Additionally, limits at infinity connect directly to horizontal asymptotes, since a horizontal asymptote is often found by evaluating \lim_{x \to \infty} f(x) or \lim_{x \to -\infty} f(x).
Evaluating Limits at Infinity
Many students wonder how to evaluate limits at infinity correctly. Several tools are used, depending on the type of function:
- Polynomial functions: Focus on the leading term, since higher powers dominate as x becomes large.
- Rational functions: Determine which part (numerator or denominator) grows faster.
- Exponential functions: Compare exponential rates of growth with polynomial or other expressions.
Example 1: Step-by-Step (Polynomial)
Evaluate \lim_{x \to \infty} (2x^3 + 5x - 1).
- Identify the highest power of x in the expression. It is x^3.
- Observe that 2x^3 grows much faster than 5x or -1.
- As x \to \infty, the term 2x^3 dominates. Therefore, \lim_{x \to \infty} (2x^3 + 5x - 1) = \infty because the function grows without bound.
Hence, the function does not settle to a finite number but instead increases endlessly.
Example 2: Step-by-Step (Rational Function)
Evaluate \lim_{x \to \infty} \frac{3x^2 - 4x + 7}{6x^2 + 5}.
- Identify the highest power of x in the numerator and denominator. Both are x^2.
- Divide each term by x^2 to compare leading coefficients: \frac{3x^2 - 4x + 7}{6x^2 + 5} = \frac{x^2(3 - \frac{4}{x} + \frac{7}{x^2})}{x^2(6 + \frac{5}{x^2})} = \frac{3 - \frac{4}{x} + \frac{7}{x^2}}{6 + \frac{5}{x^2}}.
- As x \to \infty, the terms \frac{4}{x}, \frac{7}{x^2}, and \frac{5}{x^2} go to zero.
- Therefore, the limit simplifies to \frac{3}{6} = \frac{1}{2}.
Consequently, \lim_{x \to \infty} \frac{3x^2 - 4x + 7}{6x^2 + 5} = \frac{1}{2}, showing how to evaluate limits at infinity for a rational function.
Understanding Horizontal Asymptotes
A horizontal asymptote is a horizontal line that a function approaches as x moves toward positive or negative infinity. In other words, y = L is a horizontal asymptote if \lim_{x \to \infty} f(x) = L or \lim_{x \to -\infty} f(x) = L. Horizontal asymptotes characterize the end behavior of functions. Even if a function never actually reaches that line, it gets closer and closer to it as x grows in magnitude.
Example 3: Step-by-Step (Finding a Horizontal Asymptote)
Find the horizontal asymptote of f(x) = \frac{2x^3 - x + 6}{x^3 + 5}.
- Compare the degrees of the numerator and denominator. Here, the numerator and denominator both have degree 3.
- When the degrees match, look at the ratio of the leading coefficients. The leading term in the numerator is 2x^3, and the leading term in the denominator is x^3.
- The ratio of the leading coefficients is \frac{2}{1} = 2.
- Therefore, the horizontal asymptote is y = 2.
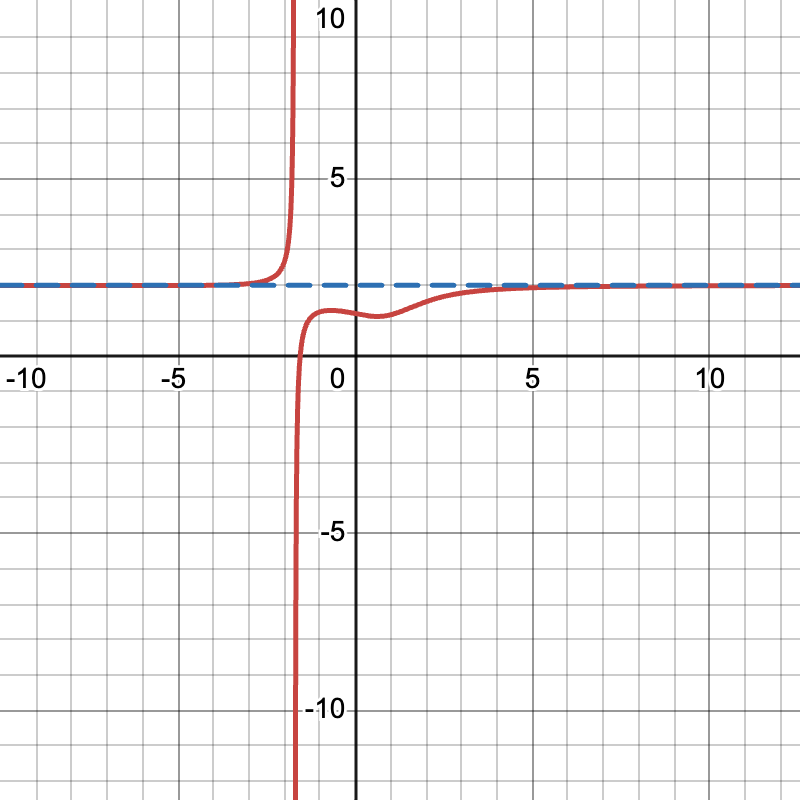
Thus, as x \to \infty or x \to -\infty, the function approaches 2.
Comparing Relative Magnitudes of Functions
Sometimes, evaluating limits at infinity is necessary to compare how fast different functions grow. For instance, exponential functions often outpace polynomials when x becomes very large. Meanwhile, polynomials can grow faster than logarithmic functions.
Therefore, using limits at infinity to compare growth rates simplifies decisions about which term dominates. This helps predict the behavior of combined expressions or more complex functions.
Example 4: Step-by-Step (Comparing Two Functions)
Compare the growth behavior of g(x) = x^2 and h(x) = 2^x as x \to \infty.
- Form the limit \lim_{x \to \infty} \frac{x^2}{2^x} to see which function grows faster.
- Notice that 2^x is exponential, while x^2 is a polynomial. Exponential functions generally grow faster than polynomials.
- To confirm, rewrite the limit using known techniques such as L’Hôpital’s rule, or recognize that exponential growth eventually surpasses any fixed power of x.
- Consequently, \lim_{x \to \infty} \frac{x^2}{2^x} = 0. This means 2^x grows more quickly than x^2.
Hence, for large x, 2^x becomes significantly larger than x^2.
Quick Reference Chart: Vocabulary and Definitions
| Term | Definition/Explanation |
| Limit at Infinity | The value a function approaches as x goes to positive or negative infinity. |
| Horizontal Asymptote | A horizontal line that a function approaches as x tends to infinity or negative infinity. |
| End Behavior | How a function behaves or trends as x gets very large (positively or negatively). |
| Dominant Term | The term that grows fastest in a function and largely determines the function’s behavior at infinity. |
Conclusion
A thorough understanding of limits at infinity serves as a foundation for 1.15 limits at infinity and horizontal asymptotes in AP® Calculus AB-BC. By knowing how to evaluate limits at infinity, students can better predict end behavior and determine whether a function settles near a specific horizontal line. These skills become crucial in more advanced topics, such as infinite series, improper integrals, and other areas where the behavior of a function at large values of x matters. Consequently, mastery of these core ideas paves the way for success in higher-level calculus and beyond.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 1.14 Connecting Infinite Limits and Vertical Asymptotes
- 1.16 Working with the Intermediate Value Theorem (IVT)
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








