What We Review
Understanding the mean value theorem for integrals is essential for mastering AP® Calculus. This article discusses the difference between the mean value theorem for derivatives and the mean value theorem for integrals. It also highlights the average value of a function, explains the average value formula calculus, and shows how to find the average value of a function step by step.
Below, each concept is broken down into smaller parts. Examples are included to illustrate how the formula works in practice. By the end, there will be a solid understanding of these ideas, along with a quick reference chart to reinforce the main points.
Foundations of the Mean Value Theorem for Integrals
Definition and Explanation
The mean value theorem for derivatives ensures there is a point on a continuous and differentiable interval where the instantaneous rate of change equals the overall rate of change. However, the mean value theorem for integrals focuses on the average value of a function.
In other words, the mean value theorem for integrals guarantees that for a continuous function f(x), there is a special point c in the interval [a, b] where f(c) equals the average value of the function on that interval. Therefore, it is directly connected to the concept of the average value of a function.
Key Idea
The average value of a continuous function f(x) on [a, b] is given by the formula:
(\frac{1}{b - a}) \int_{a}^{b} f(x) dxThis formula is often called the “average value formula calculus” because it is a fundamental way to compute how to find the average value of a function across any interval.
Steps to Find the Average Value of a Function
Overview of the Process
Finding the average value of f(x) on [a, b] involves:
- Identify the function f(x).
- Determine the interval [a, b].
- Set up the integral \int_{a}^{b} f(x) dx.
- Divide the result of the integral by (b - a).
Interpretation of the Result
The resulting number represents a “typical” value of the function on that interval. For instance, if a function’s average value is 5, it means the function behaves “as if” it is 5 all the time over the interval. This interpretation becomes useful when solving word problems or analyzing behavior in real-world contexts.
Example 1: Demonstrating the Average Value Formula
Problem Statement
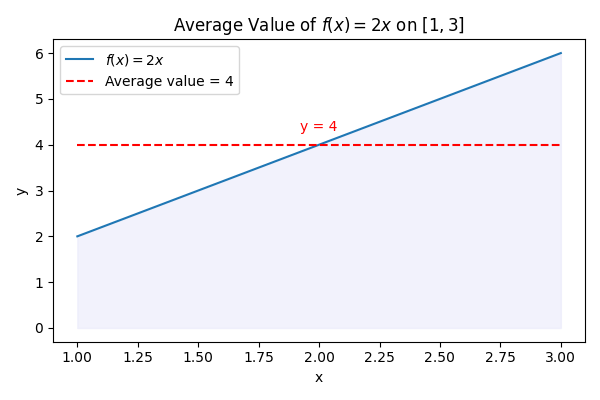
Find the average value of the function f(x) = 2x on the interval [1, 3].
Step-by-Step Solution
- Write the integral for f(x) from 1 to 3: \int_{1}^{3} 2x dx
- Compute the integral: \int_{1}^{3} 2x dx = \left[ x^2 \right]_{1}^{3} = 3^2 - 1^2 = 9 - 1 = 8
- Divide by (b - a), which is (3 - 1) = 2: \frac{8}{2} = 4
- Conclude that the average value of the function on [1, 3] is 4.
This result suggests that the function 2x acts “as if” it has a constant value of 4 on the interval [1, 3].
Example 2 (Varied Difficulty)
Problem Statement
Find the average value of the function f(x) = x^2 + 1 on the interval [0, 2].
Step-by-Step Solution
- Write the integral for f(x) from 0 to 2:
- \int_{0}^{2} (x^2 + 1) dx
- Carefully compute the integral:
- \int_{0}^{2} (x^2 + 1) dx = \left[ \frac{x^3}{3} + x \right]_{0}^{2} = \left( \frac{2^3}{3} + 2 \right) - \left( \frac{0^3}{3} + 0 \right)
- = \left( \frac{8}{3} + 2 \right) - 0 = \frac{8}{3} + 2 = \frac{8}{3} + \frac{6}{3} = \frac{14}{3}
- Divide the result by (b - a), which is (2 - 0) = 2:
- \frac{14}{3} \div 2 = \frac{14}{3} \times \frac{1}{2} = \frac{14}{6} = \frac{7}{3}
- Conclude that the average value of the function on [0, 2] is \frac{7}{3}.
Thus, the function x^2 + 1 has an average value of \frac{7}{3} or approximately 2.333 over the interval.
Common Mistakes and Helpful Tips
Mistakes to Avoid
- Forgetting to divide by (b - a).
- Mixing up the interval endpoints when setting up the integral.
- Neglecting proper integration, which leads to incorrect answers.
Tips for Accuracy
- Carefully label each step.
- Rewrite each expression clearly.
- Double-check integration work before dividing.
- Always confirm the interval boundaries and signs when integrating.
Quick Reference Chart
| Term | Definition |
| Mean Value Theorem for Integrals | Ensures there is at least one point c in [a, b] where f(c) equals the average value of the function. |
| Average Value of a Function | A number representing the “typical” or mean output of f(x) on [a, b]. |
| Average Value Formula Calculus | (\frac{1}{b - a}) \int_{a}^{b} f(x) dx |
Conclusion
In summary, the mean value theorem for integrals shows that for any continuous function on [a, b], there is at least one point where the function’s value equals its overall average value. Mastering this concept provides a deep understanding of how integrals measure accumulated quantities and how average values emerge from these accumulations.
Regular practice in setting up the integral correctly and dividing by (b - a) is vital. By following the step-by-step process to find the average value of a function, anyone can approach AP® Calculus AB-BC problems with greater confidence.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








