Geometry reasoning shows up on almost every SAT® Math section. Yet, many students find formal proofs, triangle proofs​, and dilations tricky. Fortunately, mastering these three ideas (proofs, theorems, and scale factors) can raise both speed and accuracy. This guide breaks the content into bite-sized steps. Each part includes a worked example, plus a similar practice problem you can try right away.

Why the SAT® Loves Geometry Reasoning

Because multiple-choice questions can hide small logic gaps, the test writers lean on triangle facts, parallel-line properties, and similarity shortcuts. Therefore, students who recognize a classic theorem can often solve a question in under 60 seconds.

Key benefits of solid proof skills:

• Easier elimination of wrong answer choices.
• Faster set-up of proportions in scale-factor problems.
• Higher confidence when diagrams look messy.

What the SAT® Really Tests

Although the College Board never says “Write a full proof,” it does expect these skills:

• Identify congruent parts of triangles.
• Decide when two triangles are similar under a dilation.
• Pick the missing statement or reason that completes a partial proof.

Common College Board wording includes:

• “Which of the following must be true?”
• “What value of x satisfies…?”
• “Which statement completes the proof?”

Keep reading for the exact tools you need.

The Proof Toolkit

Essential Vocabulary

• Statement: a claim about a figure (example: “AB = CD”).
• Reason: the theorem or fact that justifies the statement.
• Given: information already known.
• To Prove: the goal of the proof.

Two-Column vs. Flowchart Proofs

SAT® questions rarely ask for a full diagram, yet knowing both styles helps you trace logic:

Two-Column	Lists statements in the left column and reasons in the right.
Flowchart	Uses boxes and arrows that branch whenever two facts lead to one conclusion.
Paragraph	A logical explanation written in complete sentences that uses definitions, properties, postulates, and previously proven statements to justify each step in a geometric argument

Mini Proof Example

In \triangle ABC and \triangle DEC below, \angle ABC \cong \angle DCE and \overline{BC} \cong \overline{CE}. Prove \triangle ABC \cong \triangle DEC.

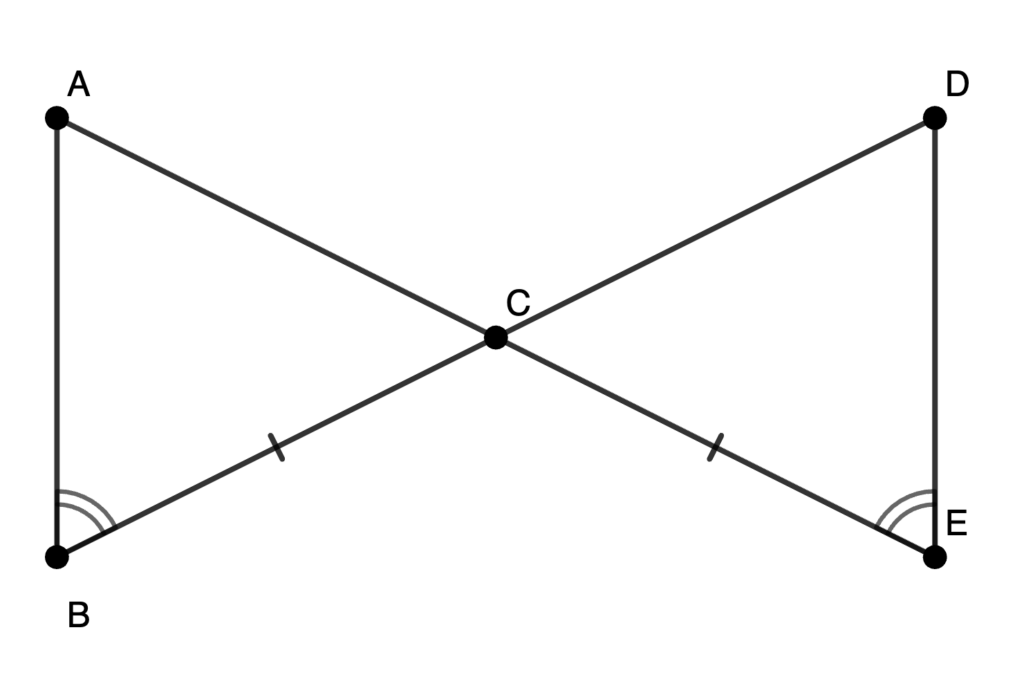
Solution

Statement	Reason
\angle ABC \cong \angle DEC	Given
\overline{BC} = \overline{CE}	Given
\angle ACB \cong \angle DCE	Vertical Angle Theorem
\triangle ABC \cong \triangle DEC	ASA (Angle-Side-Angle) Congruence

Must-Know Theorems for Triangle Congruence

Congruence Criteria You Must Recognize

• SSS (Side-Side-Side)
• SAS (Side-Angle-Side)
• ASA (Angle-Side-Angle)
• AAS (Angle-Angle-Side)
• HL (Hypotenuse-Leg for right triangles)

The Often-Hidden Vertical Angle Theorem

Whenever two lines cross, opposite (vertical) angles are equal.

Triangle Angle-Sum Theorem

For any triangle, m\angle A + m\angle B + m\angle C = 180^\circ.

Example: Find a Missing Side

In \triangle XYZ, m\angle X = 2x^\circ, m\angle Y = (x + 30)^\circ, and m\angle Z = (3x)^\circ. Find the measure of each angle.

Solution:

Using the Triangle Angle Sum Theorem, sum the angle measures to 180^\circ.

2x + (x + 30) + 3x = 180	Triangle Angle Sum Theorem
2x + x + 30 + 3x = 180	Remove parentheses
6x + 30 = 180	Combine like terms
6x = 150	Subtract 30 from both sides
x = 25	Divide both sides by 6

Now substitute x = 25:

• m\angle X = 2x = 50^\circ
• m\angle Y = x + 30 = 55^\circ
• m\angle Z = 3x = 75^\circ

m\angle X = 50^\circ, m\angle Y = 55^\circ, m\angle Z = 75^\circ.

Practice Problem 1

In two right triangles, the hypotenuse and one leg match. Which theorem proves they are congruent? (Answer at the end of the post.)

Must-Know Theorems for Triangle Similarity

Similarity Criteria

• AA (Angle-Angle)
• SAS\sim (proportional Side-Angle-Side)
• SSS\sim (proportional Side-Side-Side)

Parallel Lines & Proportional Segments

If a line parallel to one side of a triangle intersects the other two sides, it creates a smaller, similar triangle. Consequently, corresponding sides are in proportion.

Example: Validate a Proportion

In \triangle ABC, \overline{DE} is drawn parallel to \overline{BC} with D on \overline{AB} and E on \overline{AC}. Given AD = 3 and DB = 5, show \dfrac{AD}{AB} = \dfrac{AE}{AC}.

Solution:

Since \overline{DE} \parallel \overline{BC}, angle \angle ADE \cong \angle ABC and angle \angle DEA \cong \angle BCA by the Corresponding Angles Postulate. So, by the AA Similarity Theorem, triangles \triangle ADE and \triangle ABC are similar.

Because the triangles are similar, their corresponding sides are proportional:
\dfrac{AD}{AB} = \dfrac{AE}{AC} = \dfrac{DE}{BC}.

Thus, \dfrac{AD}{AB} = \dfrac{AE}{AC}.

Practice Problem 2

Using the same diagram, if AE = 4 and AC = 10, find DE:BC. (Answer at the end of the post.)

Scale Factors and Dilations

What Changes and What Stays the Same

A dilation with scale factor k:

• Multiplies every length by k.
• Keeps every angle measure unchanged.
• Therefore, area changes by k^2 and volume by k^3.

Length, Perimeter, Area, and Volume

Measure	New Value after Dilation	Example with k = 3
Length	\text{old}\times k	2 \text{ cm}\rightarrow 6 \text{ cm}
Perimeter	\text{old}\times k	10 \text{ cm}\rightarrow 30 \text{ cm}
Area	\text{old}\times k^2	4 \text{ cm}^2\rightarrow 36 \text{ cm}^2
Volume	\text{old}\times k^3	1 \text{ cm}^3\rightarrow 27 \text{ cm}^3

Example: Find Missing Measures

A rectangle is dilated by k = \dfrac{5}{2}. The original width is 8 cm and the area is 64 \text{ cm}^2. Find the new width and area.

Solution:

To find the new width, multiply the original width by the scale factor:

8 \times \dfrac{5}{2} = 20 \text{ cm}

The area changes by the square of the scale factor:

k^2 = \left(\dfrac{5}{2}\right)^2 = \dfrac{25}{4}

Multiply the original area by this factor:

64 \times \dfrac{25}{4} = 64 \times 6.25 = 400 \text{ cm}^2

So, the new width is 20 cm and the new area is 400 \text{ cm}^2.

Practice Problem 3

After a dilation with k = 0.6, a triangle’s perimeter becomes 18 cm. What was the original perimeter? (Answer at the end of the post.)

Picking the Missing Statement in an SAT® Proof Question

Common Multiple-Choice Formats

• “Which statement completes the proof?”
• “Which reason justifies Step 3?”

Elimination Tricks and Time-Savers

• Check which parts are already cited as “Given.” Eliminate any answer that repeats them.
• Look at the final target statement; therefore, work backward to see which fact is still missing.
• When two triangles share a side, the reflexive property appears surprisingly often.

Example: Partial Proof

Statement	Reason
1. \overline{AC} \parallel \overline{DE}	Given
2. \angle BAC \cong \angle E	?
3. \triangle ABC \sim \triangle DEF	AA Similarity

Solution

Because \overline{AC} \parallel \overline{DE}, corresponding angles are equal. Therefore, Statement 2 is true by the Corresponding Angles Postulate.

Practice Problem 4

If lines \overline{m} and \overline{n} are parallel, which angle relationship is always true?

Mixed Practice: One Problem, Many Tools

In the diagram, \overline{GH} is parallel to \overline{JK}. Triangle \triangle GHI is a dilation of \triangle JKI with center I and scale factor k = 1.5. If JK = 10 cm and KI = 8 cm, find GH and HI.

Solution:

Because of the dilation with center I, points G and J as well as H and K lie on the same rays from I. This means the corresponding sides and angles of the triangles align through a proportional transformation.

Therefore, \triangle GHI \sim \triangle JKI by the definition of dilation.

The scale factor of the dilation is k = \dfrac{IG}{IJ} = 1.5.

Since GH corresponds to JK, we calculate:

GH = 1.5 \times 10 = 15 \text{ cm}

Similarly, HI corresponds to KI, so:

HI = 1.5 \times 8 = 12 \text{ cm}

Practice Problem 5

If the scale factor had been k = \dfrac{2}{3} instead, what would GH equal?

Quick Reference Vocabulary Chart

Term	Definition / Key Idea
Congruent Triangles	Triangles with exactly equal corresponding sides and angles.
Similar Triangles	Triangles with equal angles and proportional sides.
Dilation	Transformation that produces a similar figure by scale factor k.
Scale Factor k	The multiplier that is applied to every length in a dilation.
Corresponding Angles	Angles in matching positions when a transversal cuts parallel lines are equal.
Alternate Interior Angles	Interior angles on opposite sides of a transversal are equal if the lines are parallel.
Vertical Angles	Opposite angles formed by two intersecting lines are always equal.
Triangle Angle-Sum	Interior angles of a triangle add to 180^\circ.
SSS, SAS, ASA, AAS, HL	Shortcuts for proving triangle congruence.
AA~, SAS~, SSS~	Shortcuts for proving triangle similarity.
Proportion	Equation showing that the two ratios are equal.
Reflexive Property	Any segment or angle is congruent to itself.
Two-Column Proof	Proof format listing statements and matching reasons.
Flowchart Proof	A diagrammatic proof showing logical connections with arrows.
Perimeter Change	Multiplied by k under dilation.

Practice Problem Solutions

1. HL
2. \dfrac{2}{5}
3. 30 \text{ cm}
4. Alternate interior angles are congruent
5. 6 \text{ cm}

Final Tips & Next Steps

Therefore, keep these habits to lock in the material:

• Rewrite each theorem on an index card; quiz yourself daily.
• Sketch quick diagrams when practicing; visual memory helps recall.
• Time yourself on five official SAT® geometry questions to build speed.

Next, explore more targeted sets focusing on “proofs, theorems, and scale factors.” Reliable sources include the College Board Question Bank and reputable practice sites. Master these concepts now, and watch your SAT® Math score climb.

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.